Синусоида – свойства, формула и график функции

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №4. Свойства и график функции .

Перечень вопросов, рассматриваемых в теме

Изучение свойств графика функции ;
Определение промежутков монотонности, наибольшего и наименьшего значения, нулей функции ;
Определение свойств и положение графика тригонометрических функций вида и
Построение графика функции
Объяснять зависимость свойств и положения графика функции вида иот значения коэффициентов а, k, b;
Демонстрирование уверенного владения свойствами функции .

Глоссарий по теме

Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции , где a≠0.

Число │a│ называется амплитудой.

Основная литература:

Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

На прошлом уроке мы говорили о свойствах графика косинуса:

1) область определения функции – множество R всех действительных чисел;

2) Множество значений функции – отрезок [–1;1];

3) Функция косинуса периодическая, ;

4) Функция чётная;

5) Функция принимает:

значение, равное 0, при ;
наименьшее значение, равное –1, при

;

наибольшее значение, равное 1, при ;

6) Функция

возрастает на отрезке и на отрезках, получаемых сдвигами этого интервала на .

Давайте сравним их со свойствами графика синуса, а для начала определим следующие моменты:

При движении точки до первой четверти ордината увеличивается;
При движении точки по второй четверти ордината постепенно уменьшается;
Функция возрастает на отрезке и убывает на отрезке .

Свойства функции :

3) Период функции равен ;

4) Функция чётная/нечётная;

5) Функция принимает:

значение, равное 0, при ;
наименьшее значение, равное –1, при ;
наибольшее значение, равное 1, при ;
положительные значения на интервале (0;) и на интервалах, получаемых сдвигами этого интервала на ;
отрицательные значения на интервале и на интервалах, получаемых сдвигами этого интервала на .

6) Функция

возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на ;
убывает на отрезке и на отрезках, получаемых сдвигами этого отрезка на .

Изменяя амплитуду и значение аргумента функции синуса график ведет себя следующим образом (рис.1)

Рис. 1 – графики синуса

Сдвиг графика влево/вправо вдоль оси абсцисс

Если к аргументу функции добавляется постоянная, то происходит сдвиг (параллельный перенос) графика вдоль оси Ох.

Правило:
1) чтобы построить график функции , нужно сдвинуть график вдоль оси Ох на b единиц влево;

2) чтобы построить график функции , нужно график сдвинуть вдоль оси ОХ на b единиц вправо.

Теоретический материал для самостоятельного изучения

1. На следующие утверждения нужно ответить верно/неверно.

1) Тригонометрическая функция определена на всей числовой прямой.

2) График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.

3) График тригонометрической функции можно построить, используя одну главную полуволну.

Ответ: верно, неверно, верно.

2. Вспомним, что мы уже знаем о функции , ответив на вопросы:

1) Какие значения может принимать переменная х. Какова область определения этой функции?

2) В каком промежутке заключены значения выражения . Назови наибольшее и наименьшее значения функции .

3) Функция синуса чётная или нечётная?

Примеры и разборы решения заданий тренировочного модуля:

Пример 1. Найдем все корни уравнения , принадлежащие отрезку .

Построим графики функций и (рис. 6)

Рис. 7 – графики функций и .

Графики пересекаются в четырёх точках, абсциссы которых являются корнями уравнения . На выбранном отрезке от корни уравнения симметричны: и . Из рисунка видно, что симметричность корней объясняется периодичностью функции: аналогично для

Ответ: ; .

Пример 2.Найти все решения неравенства , принадлежащие отрезку .

Из рисунка 7 видно, что график функции лежит выше графика функции на промежутках и и

Ответ: , ,

Тригонометрические функции

В школьной программе изучаются четыре тригонометрических функции – синус, косинус, тангенс и котангенс. В этой статье мы рассмотрим графики и основные свойства этих функций.

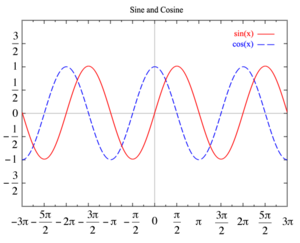
1. Начнем с построения графика функции y = sin x.

Выберем подходящий масштаб. По оси X: три клетки примем за (это примерно полтора). Тогда – одна клеточка, – две клетки.
По оси Y : две клетки примем за единицу.

Область определения функции y = sin x – все действительные числа, поскольку значение sin α можно посчитать для любого угла α.

Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.

Можем добавить, для большей плавности графика, точки и . В них значение синуса равно
Соединим полученные точки плавной кривой.

Мы помним, что . Это значит, что
Получается часть графика, симметричная той, которую нарисовали раньше.

Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть

Это значит, что функция y = sin x является периодической. Мы уже построили уча-сток графика длиной 2π. А теперь мы как будто “копируем” этот участок и повторяем его с периодом 2π:

Синусоида построена.
Перечислим основные свойства функции y = sin x.

1) D(y): x ∈ R, то есть область определения – все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее – минус единице.

3) Функция y = sin x – нечетная. Ее график симметричен относительно нуля.

4) Функция y = sin x – периодическая. Ее наименьший положительный период равен 2π.

2. Следующий график: y = cos x. Масштаб – тот же. Отметим на графике точки, в которых косинус является рациональным числом:

Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y , то есть левая его часть будет зеркальным отражением правой.

Функция y = cos x – тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. “Копируем” участок графика, который уже построили, и повторяем периодически.

Перечислим основные свойства функции y = cos x.

1) D(y): x ∈ R, то есть область определения – все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее – минус единице.

3) Функция y = cos x – четная. Ее график симметричен относительно оси Y .

4) Функция y = cos x – периодическая. Ее наименьший положительный период равен 2π.

Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на влево. Так оно и есть – по одной из формул приведения, .

Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!

Функции синус и косинус идеально подходят для описания колебаний и волн – то есть процессов, повторяющихся во времени.

По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I cos(ωt+α). Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того – объекты микромира (например, электрон) проявляют волновые свойства.

3. Перейдем к графику функции y = tg x.

Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же – три клетки по оси X соответствуют , две клетки по Y – единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функ-ция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.

Непонятно только, как быть с точкой . Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к , то есть к 90 градусам?

Чтобы ответить на этот вопрос, возьмем значение x, близкое к , и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть .

Синус угла – это почти 1. Точнее, sin = 0,9998. Косинус этого угла близок к нулю. Точнее, cos = 0,0175.

Тогда
график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к (то есть к , значение функции y = tg x стремится к бесконечности .

Аналогично, при x, близких к , график тангенса уходит вниз, то есть стремится к минус бесконечности .

Осталось только “скопировать” этот участок графика и повторить его с периодом π.

Перечислим свойства функции y = tg x.

1) .
Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) – все действительные числа.

3) Функция y = tg x – нечетная. Ее график симметричен относительно начала координат.

4) Функция y = tg x – периодическая. Ее наименьший положительный период равен π.

5) Функция y = tg x возрастает при то есть на каждом участке, на котором она непрерывна.

4. График функции y = ctg x строится аналогично. Вот он:

1) .
Другими словами, котангенс не определен для где n ∈ Z.
2) Область значений E(y) – все действительные числа.

3) Функция y = сtg x – нечетная. Ее график симметричен относительно начала координат.

4) Функция y = сtg x – периодическая. Ее наименьший положительный период равен π.

5) Функция y = сtg x убывает при то есть на каждом участке, на котором она непрерывна.

Функция y = sin x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).

Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x синусоидой .
Часть синусоиды для 0≤x≤2π называют волной синусоиды .
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды .

п.2. Свойства функции y=sinx⁡

1. Область определения (xinmathbb) – множество действительных чисел.

2. Функция ограничена сверху и снизу

Область значений (yin[-1;1])

3. Функция нечётная

4. Функция периодическая с периодом 2π

5. Максимальные значения (y_=1) достигаются в точках

Минимальные значения (y_=-1) достигаются в точках

Нули функции (y_<0>=sinx_0=0) достигаются в точках (x_0=pi k)

6. Функция возрастает на отрезках

$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$

Функция убывает на отрезках

$$ fracpi2+2pi kleq xleqfrac<3pi><2>+2pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:

a) (left[fracpi6; frac<3pi><4>right]) $$ y_=sinleft(fracpi6right)=frac12, y_=sinleft(fracpi2right)=1 $$ б) (left[frac<5pi><6>; frac<5pi><3>right]) $$ y_=sinleft(frac<3pi><2>right)=-1, y_=sinleft(frac<5pi><6>right)=frac12 $$

Пример 2. Решите уравнение графически:
a) (sinx=3x)

Один корень: x = 0

б) (sinx=2x-2pi)

Один корень: x = π

в) (sinx-sqrt=0)
(sinx=sqrt)

Один корень: x = π

г*) (sinx=left(x-fracpi2right)^2-frac<4>)
(y=left(x-fracpi2right)^2-frac<4>) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -frac<4>right)) (см. §29 справочника для 8 класса)

Два корня: (x_1=0, x_2=pi)

Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$

(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) – исходная функция поднимается вверх на 2. Область значений (yin[1;3]).

Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac <2>$$

Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) – период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac<2>) – период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

стационарные и критические точки;
точки экстремума;
нули функции;
точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x – 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

x	y
0	-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

x	y
0	2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

x	y
0	0
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x – a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x – a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Синусоида

Синусо́ида — плоская кривая, задаваемая В прямоугольных координатах уравнением

График уравнения вида

также называется синусоидой; термин «косинусоида» используется редко. Данный график получается из синусоидального сдвигом на в отрицательном направлении оси абсцисс.

В приведённых формулах a, b, c, d — постоянные;

a характеризует сдвиг графика по оси Oy. Чем больше a, тем выше поднимается график;
b характеризует растяжение графика по оси Oy. Чем больше увеличивается b, тем сильнее возрастает амплитуда колебаний;
с характеризует растяжение графика по оси Ox. При увеличении c частота колебаний повышается ;
d характеризует сдвиг графика по оси Ox. При увеличении d график двигается в положительном направлении оси абсцисс.

Синусоидальное изменение какой-либо величины называется гармоническим колебанием. Примерами могут являться любые колебательные процессы начиная от качания маятника и кончая звуковыми волнами. Также синусоида — проекция на плоскость трёхмерной спирали, например, скрученного провода.

Синусоида пересекает ось абсцисс в точках . Ось ординат пересекает единожды в точке .

Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)

Wikimedia Foundation . 2010 .

Тихий, Алексей Иванович
Верность (фильм)

Полезное

Смотреть что такое “Синусоида” в других словарях:

СИНУСОИДА — плоская кривая график функции y=sin x. См. Тригонометрические функции … Большой Энциклопедический словарь

СИНУСОИДА — СИНУСОИДА, синусоиды, жен. (мат.). В высшей математике волнообразная кривая линия, графически изображающая изменение синуса в зависимости от изменения угла. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

СИНУСОИДА — кривая, характеризующая изменения синуса угла в зависимости от величины последнего. Для построения С. по горизонтали откладывают значения угла, а по вертикали соответствующие им значения синуса. В переменном токе по С. изменяются сила тока и… … Технический железнодорожный словарь

синусоида — сущ., кол во синонимов: 1 • график (17) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

синусоида — (напр. тока, напряжения) — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN sine wavesinusoidal wave … Справочник технического переводчика

Синусоида — график функции у= sin x , плоская кривая (см. рис.), изображающая изменение Синуса в зависимости от изменения его аргумента (угла). С. пересекает ось Ox в точках 180 ° k (или πk) , в точках вида 90°+360% (или π/2 + 2πk) имеет максимумы, а … Большая советская энциклопедия

СИНУСОИДА — график функции y = sin x(см. рис.). С. непрерывная кривая с периодом Т=2p. Пересечения с осью Ох точки (kp, 0); они же точки перегиба с углом +p/4 наклона к оси Ох;экстремумы ((k+1/2) p, ( 1)k). График функции y=cosx=sin(x+p/2) косинусоида… … Математическая энциклопедия

СИНУСОИДА — (от синус и греч. eidos вид) график ф ции у = sinх; волнообразная линия, графически изображающая изменение синуса в зависимости от изменения его аргумента (угла) (см. рис.). Синусоида … Большой энциклопедический политехнический словарь

синусоида — (гр. eidos вид) мат. график синуса, представляющий собой периодическую кривую волнистой формы. Новый словарь иностранных слов. by EdwART, , 2009. синусоида [синус + гр. вид] – мат. бесконечная кривая линия волнистой формы, графически изображающая … Словарь иностранных слов русского языка

синусоида — ы; ж. Матем. График синуса, представляющий собой волнистую линию. * * * синусоида плоская кривая график функции у = sinх. См. Тригонометрические функции. * * * СИНУСОИДА СИНУСОИДА, плоская кривая график функции y=sin x. См. Тригонометрические… … Энциклопедический словарь

Уроки математики и физики для школьников и родителей

суббота, 4 сентября 2021 г.

Урок 5. Периодичность тригонометрических функций

Периодические функции.

Функцию у = f (х) , х ∈ Х , называют периодической , если существует такое отличное от нуля число Т , что для любого х из области определения функции справедливо равенство:

f (х + Т) = f (х) = f (х – Т) .

Число Т называют периодом функции у = f (х) .

Из этого определения сразу следует, что если Т – период функции

у = f (х) , то

2Т, 3Т, 4Т, –Т, –2Т, –3Т, –4Т

– также периоды функций. Значит у периодической функции бесконечно много периодов.

Если Т – период функции, то число вида k Т , где k – любое целое число, также является периодом функции.

Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом .

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

Графики периодических функций обладают следующей особенностью. Если Т – основной период функции у = f (х) , то для построения её графика достаточно построить ветвь графика на одном из промежутков оси х длиной Т , а затем осуществить параллельный перенос этой ветви по оси х на

± Т, ± 2Т, ± 3Т, …

(– Т / ₂ ; 0) и ( Т / ₂ ; 0) или

(0; 0) и (Т; 0) .

Рассмотрим функцию

у = х – [х] , где [х] – целая часть числа. Если к произвольному значение аргумента этой функции добавить 1 , то значение функции от этого не изменится :

f (x + 1) = (x +1) – [x + 1] = x + 1 – [x] – 1 = x – [x] = f (x).

Следовательно, при любом значении х

f (x + 1) = f(x).

А это значит, что рассматриваемая функция периодическая, период которой равен 1 . Любое целое число также является периодом данной функции, но обычно рассматривают только маленький положительный период функции.

Возьмём произвольный угол α и построим подвижной радиус ОМ единичной окружности такой, что угол, составленный с осью Ох этим радиусом, равен α .

Если мы к углу прибавим 2π или 360 ° (то есть полный оборот), то углу α + 2π или α + 360 ° будет соответствовать то же положение подвижного радиуса ОМ , что для угла α .

sin (α + 2π) = sin α или

sin (α + 360 ° ) = sin α

cos (α + 2π) = cos α или

cos (α + 360 ° ) = cos α .

Таким образом, функции sin α и cos α от прибавления к аргументу α одного полного оборота ( 2π или 360 ° ) не меняют своих значений.

Точно так же, прибавляя к углу α любое целое число полных оборотов, мы не изменим положения подвижного радиуса ОМ , а потому:

sin (α + 2 k π ) = sin α или

sin (α + 360 ° k ) = sin α

cos (α + 2 k π ) = cos α или

cos (α + 360 ° k ) = cos α ,

где k – любое целое число.

Функции, обладающие таким свойством, что их значения не изменяются от прибавления к любому допустимому значению аргумента определённого постоянного числа, называются периодическими .

Следовательно, функции sin α и cos α – периодические.

Наименьшее положительное число, от прибавления которого к любому допустимому значению аргумента не изменяется значение функции, называется периодом функции.

Периодом функции sin α и cos α является 2π или 360 ° .

Функции tg α и с tg α также периодические и их периодом является число π или 180 ° .

В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным радиусом ОМ единичной окружности.

Построим точку М ‘,

Если х и у – координаты точки М , то точки М ‘ будут –х и –у . Поэтому

sin α = у, cos α = х,

sin (α + π) = –у,

cos (α + π) = –х.

tg (α + π) = tg α,

с tg (α + π) = с tg α .

отсюда следует, что значения tg α и с tg α не изменяются, если к углу α прибавить любое число полуоборотов:

tg (α + k π ) = tg α,

с tg (α + k π ) = с tg α .

где k – любое целое число.

y = A sin ( ωx + φ ) и

y = A cos ( ωx + φ )

вычисляются по формуле

T = 2π /_ω ,

а период функции

y = A tg ( ωx + φ )

T = π /_ω .

Если период функции y = f ( x ) равен T ₁ , а период функции y = g ( x ) равен T ₂ , то период функций

y = f ( x ) + g ( x ) и

y = f ( x ) – g ( x )

равен наименьшему числу, при делении которого на T ₁ и T ₂ получаются целые числа.

Найти период функции

y = 3 sin (x – 2) + 7 со s π x .

Период функции

y = 3 sin ( x – 2)

T ₁ = 2π / 1 = 2π .

Период функции

y = 7 со s π x

Периода у функции

y = 3 sin ( x – 2) + 7 со s π x

не существует, так как такого числа, при делении которого на 2π и на 2 получались бы целые числа, нет.

Периода не существует.

Доказать следующее утверждение :

tg 3850 ° = tg 250 ° .

Так как тангенс – периодическая функция с минимальным периодом 20 ∙ 180 ° , то получим :

tg 3850 ° = tg (20 ∙ 180 ° + 250 ° ) = tg 250 ° .

Доказать следующее утверждение :

сos (–13π) = –1.

Так как косинус – чётная и периодическая функция с минимальным периодом 2π , то получим :

сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.

Доказать следующее утверждение :

sin (–7210 ° ) = – sin 10 ° .

Так как синус – нечётная и периодическая функция с минимальным периодом 20 ∙ 360 ° , то получим :

sin (–7210 ° ) = –sin 7210 ° = –sin (20 ∙ 360 ° + 10 ° ) – sin 10 ° .

ПРИМЕР :

Найти основной период функции

Пусть Т основной период функции, тогда:

sin 7х = sin 7(х + t ) = sin (7х + 7 t )

так как 2 πk период синуса, то получим :

sin (7х + 7 t ) = sin (7х + 2 πk ),

Найти основной период функции

Пусть Т основной период функции, тогда:

со s 0,3х = со s 0,3(х + t ) = со s (0,3х + 0,3 t )

так как 2 πk период косинуса, то получим :

со s (0,3х + 0,3 t ) = со s (0,3х + 2 πk ),

Найти период функции :

y = 5 sin 2 x + 2 ctg 3х.

Период функции

y = 5 sin 2 x

равен Т ₁ = 2 / ₂ = π ,

а период функции

y = 2 ctg 3х

равен Т ₂ = / ₃ .

Наименьшее число, при делении которого на

Т ₁ = π и Т ₂ = / ₃

– получаются целые числа будет число π . Следовательно, период заданной функции равен Т = π .

Найти период функции :

y = 9 sin (5 x + π / ₃ ) – 4 c о s (7х + 2).

Находим периоды слагаемых. Период функции

y = 9 sin (5 x + π / ₃ )

равен Т ₁ = 2 / ₅ ,

а период функции

y = 4 c о s (7х + 2)

равен Т ₂ = 2 / ₇ .

Очевидно, что период заданной функции равен

Т = 2π .

Найти период функции :

y = 3 sin π x + 8 tg (х + 5).

Период функции

y = 3 sin π x

равен Т ₁ = 2 π / _π = 2,

а период функции

y = 8 tg (х + 5)

равен Т ₂ = / ₁ = π.

Периода у заданной функции не существует, так как нет такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.

Найти период функции :

y = sin 3 x + со s 5х.

Период функции

y = sin 3 x

равен Т ₁ = 2 π / ₃ ,

а период функции

y = со s 5х

равен Т ₂ = 2 π / ₅ .

Приведём к общему знаменателю периоды :

Т ₁ = 10 π / ₁₅ , Т ₂ = 6 π / ₁₅ .

Тогда наименьшее общее кратное (НОК) будет :

НОК (10π; 6π) = 30π.

Теперь найдём период заданной функции :

Т = 30 π / ₁₅ = 2π .

Значение синуса, косинуса, тангенса и котангенса: их графики, описание

Содержание:

Чтобы построить графики синуса, косинуса, тангенса и котангенса, необходимо использовать систему координат. Каждый график отличается по своей структуре. Далее рассмотрим графики функций синуса, косинуса, тангенса, котангенса, а также проведем сравнение косинуса и синуса углов.

Синус как тригонометрическая функция – определение, график

Выражение у = sin х – это легкий пример тригонометрической функции. Она определяется для любого значения переменной. Область нахождения решения – все действительные числа. Присутствуют ограничения функционала в зоне интервала от -1 до 1, единицы также входят в интервал. Среднее значение области определения изменений исходит из неравенства -1 ≤ у ≤ 1

Ряд максимальных значений принимается при x = frac <2>+ 2k pi . В таком случае число функционала – 1, если x = — frac <2>+ 2k pi , выражение стремится к -1, находится в области минимальных значений -1.

Тригонометрический показатель у = sin х:

Нечетная, так как расположение синусоиды симметрично к началу системы координат;
Периодичная. Установленный период – 2 π ;
Характерно монотонное возрастание для интервала – frac <2>+ 2n pi
В интервале x = frac <2>+ 2k pi может являться наблюдается монотонное убывание;
n моет являться любым числом; Если х= кπ, выражение нулевое.

Косинус – построение графика, основные параметры

Функция cos cos х находится в области определения R, обладает множеством значений от -1 до 1. Это четное выражение с периодичностью Т=2 π . Нулевые показатели достигаются при х = frac <2>+ pi_n , если n ϵ Z. Монотонность достигается в промежутках:

х ∈ [-π + 2πn] — nϵZ – возрастание;
х ∈ [2πn,π + 2πn] — nϵZ -убывание;

Экстремальные показатели для косинуса:

У_min = -1, если x = π + 2πn
У_max = 1, если x = 2πn

n всегда принадлежит Z.

Сравнение синусов и косинусов – примеры, формулы

Чтобы сравнить некоторые данные, следует построить график синуса, косинуса, тангенса, котангенса или воспользоваться единичной окружностью. Сопоставлять аргументы с разными знаками проще, чем отрицательные или положительные функции. На рисунке видно, что вторым радианом выступает угол, находящийся во второй плоскости. По умолчанию значение синуса здесь – положительное число, косинус – отрицательный. Все положительные элементы изначально больше отрицательных. Отсюда следует, что:
sin 1 >cos 3,
sin 3 > cos 4,
sin 2 > cos 4,
sin 2 > cos 3,
sin 5 cos 1,
sin 3 sin 4,
cos 3

Функция тангенса – свойство, графическое изображение

Тангенс – сложный график нечетного типа с множеством вариантов решения R. Он находится в области вычисления: d ( tg x) = frac < R >< frac < pi > < 2 >+ pi _(n in Z) > . Основной период – Т = π. Нулевой показатель достигается при х=π_n, n ϵ Z. Экстремумы отсутствуют.

Для тангенса характерно возрастание на всех интервалах, входящих в область ее обозначения.

Тригонометрический график котангенса

Действительное число для области выявления котангенса находится во множестве Х ≠ πn при условии n ϵ Z. Общий вид периодического нечетного выражения котангенса – y = ctg x, период – :