Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
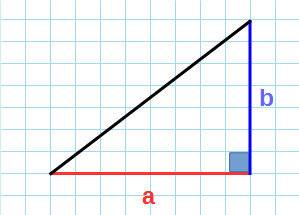
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
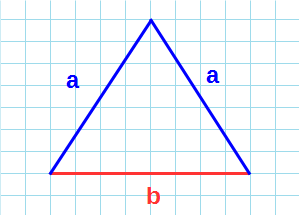
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
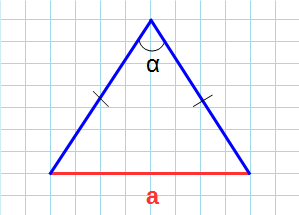
Формула нахождения площади равнобедренного треугольника через основание и угол:
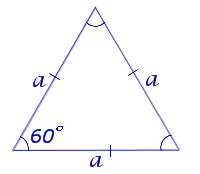
Площадь равностороннего треугольника через стороны
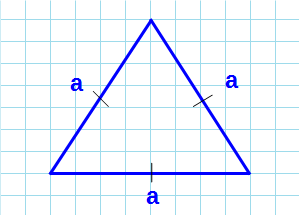
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
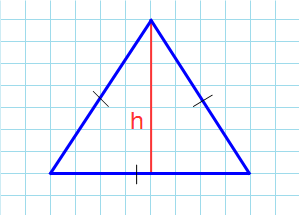
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
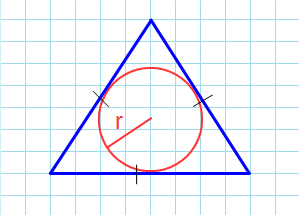
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
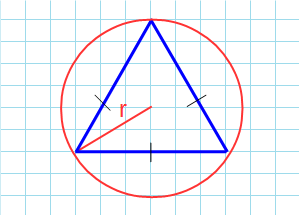
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
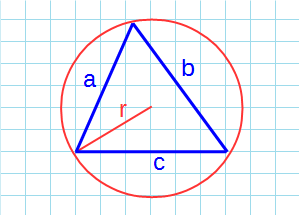
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
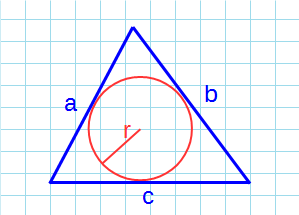
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Площадь треугольника
 Формулы для площади треугольника Формулы для площади треугольника |
 Вывод формул для площади произвольного треугольника Вывод формул для площади произвольного треугольника |
 Вывод формул для площади равностороннего (правильного) треугольника Вывод формул для площади равностороннего (правильного) треугольника |
 Вывод формул для площади прямоугольного треугольника Вывод формул для площади прямоугольного треугольника |

Формулы для площади треугольника
Формулы, позволяющие находить площадь треугольника , удобно представить в виде следующей таблицы.
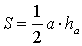
a – любая сторона,
ha – высота, опущенная на эту сторону
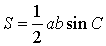
a и b – две любые стороны,
С – угол между ними
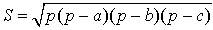
 .
.
Формулу называют «Формула Герона»
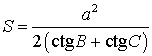
a – любая сторона,
B, С – прилежащие к ней углы
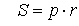
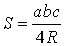
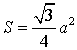
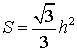
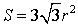
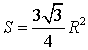
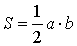
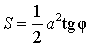
a – катет,
φ – прилежащий острый угол
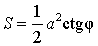
a – катет,
φ – противолежащий острый угол
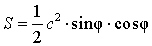
c – гипотенуза,
φ – любой из острых углов
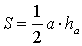
где
a – любая сторона,
ha – высота, опущенная на эту сторону
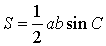
где
a и b – две любые стороны,
С – угол между ними
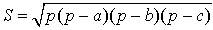
 .
.
Формулу называют «Формула Герона»
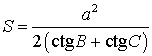
где
a – любая сторона,
B, С – прилежащие к ней углы
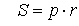
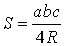
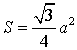
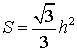
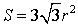
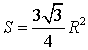
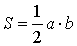
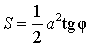
где
a – катет,
φ – прилежащий острый угол
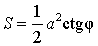
где
a – катет,
φ – противолежащий острый угол
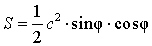
где
c – гипотенуза,
φ – любой из острых углов
| Произвольный треугольник |
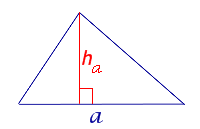 |
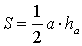
где
a – любая сторона,
ha – высота, опущенная на эту сторону
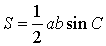
где
a и b – две любые стороны,
С – угол между ними
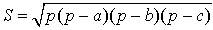
 .
.
Формулу называют «Формула Герона»
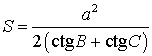
где
a – любая сторона,
B, С – прилежащие к ней углы
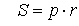
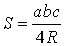
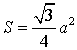
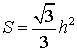
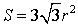
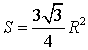
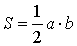
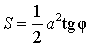
где
a – катет,
φ – прилежащий острый угол
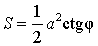
где
a – катет,
φ – противолежащий острый угол
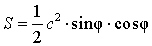
где
c – гипотенуза,
φ – любой из острых углов
Вывод формул для площади произвольного треугольника
Утверждение 1 . Площадь треугольника можно найти по формуле
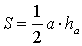
где a – любая сторона треугольника, а ha – высота, опущенная на эту сторону.
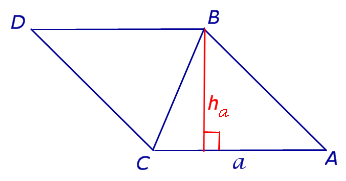
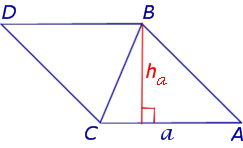
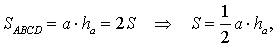
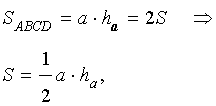
что и требовалось доказать.
Утверждение 2 . Площадь треугольника можно найти по формуле
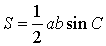
где a и b – две любые стороны треугольника, а С – угол между ними.
то, в силу утверждения 1, справедлива формула
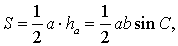
что и требовалось доказать.
Утверждение 3 . Площадь треугольника можно найти по формуле
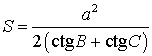
где a – любая сторона треугольника, а B, С – прилежащие к ней углы.
Замечание . Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.
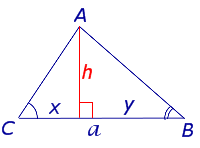
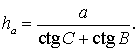
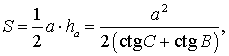
что и требовалось доказать.
Утверждение 4 . Площадь треугольника можно найти по формуле
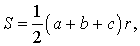
где a, b, c – стороны треугольника, а r – радиус вписанной окружности.
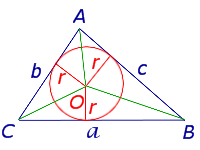
Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим
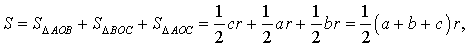
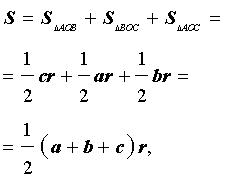
что и требовалось доказать.
Утверждение 5 . Площадь треугольника можно найти по формуле
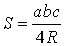
где a, b, c – стороны треугольника, а R – радиус описанной окружности.
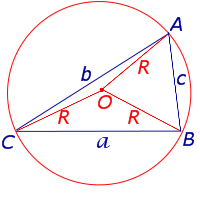
В силу теоремы синусов справедливо равенство
 .
.
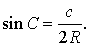
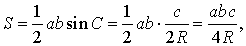
что и требовалось доказать.
Утверждение 6 . Площадь треугольника можно найти по формуле:
где A, B, С – углы треугольника, а R – радиус описанной окружности.

В силу теоремы синусов справедливо равенство
 .
.
В силу утверждения 5
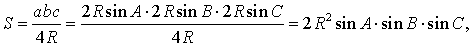
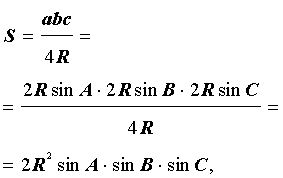
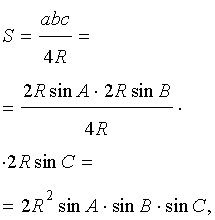
что и требовалось доказать.
Вывод формул для площади равностороннего треугольника
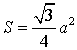
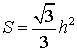
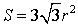
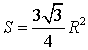
В силу утверждения 2
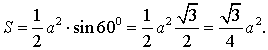

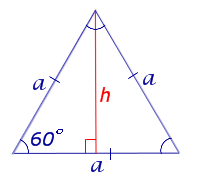
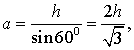
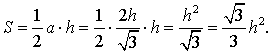
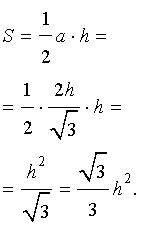
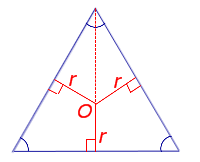
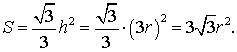
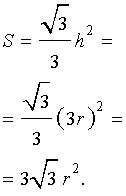
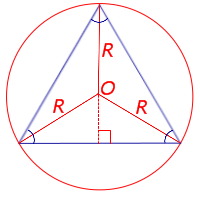
Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство 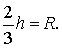 Следовательно,
Следовательно,
Как найти площадь треугольника

О чем эта статья:
Основные понятия
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Общая формула
1. Площадь треугольника через две стороны и угол между ними.
S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.
2. Площадь треугольника через основание и высоту.
S = 0,5 * a * h, где a — основание, h — высота.
3. Площадь треугольника через описанную окружность и стороны.
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны.
S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.
Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:
S = r * p, где p — полупериметр.
5. Площадь треугольника по стороне и двум прилежащим углам.
S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.
6. Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам.
S = 0,5 * a * b, где a, b — стороны.
Площадь треугольника по гипотенузе и острому углу.
S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу.
S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и по радиусу вписанной окружности.
S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.
Площадь треугольника вписанного в окружность.
Площадь прямого треугольника по формуле Герона.
S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.
Для равнобедренного треугольника
Поиск площади через основание и сторону.
S = b : 4 * √ 4 * a 2 − b 2 , где a — боковая сторона, b — основание.
Вычисление площади через основание и угол.
S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.
Вычисление площади через основание и высоту.
S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.
S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности.
S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности.
S = 3 * √ 3 * r 2 , где r — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону.
S = (√ 3 * a 2 ) : 4, где a — сторона.
Площадь равностороннего треугольника через высоту.
S = h 2 : √ 3, где h — высота.
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Площадь треугольника — формулы и калькулятор онлайн
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали 21 калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного.
Площадь треугольника
Площадь треугольника через две стороны и угол между ними

Формула для нахождения площади треугольника через 2 стороны и угол:
Площадь треугольника через основание и высоту

Формула для нахождения площади треугольника через основание и высоту:
Площадь треугольника через радиус описанной окружности и 3 стороны

Формула для нахождения площади треугольника через описанную окружность и стороны:
Площадь треугольника через радиус вписанной окружности и 3 стороны

Формула для нахождения площади треугольника через вписанную окружность и стороны:
Формулу можно переписать иначе, если учитывать, что
Площадь треугольника через сторону и два прилежащих угла

Формула для нахождения площади треугольника через сторону и 2 прилежащих угла:
Площадь треугольника по формуле Герона

Формула для нахождения площади треугольника по формуле Герона (если известны 3 стороны):
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника через 2 стороны

Формула для нахождения площади прямоугольного треугольника по двум сторонам:
Площадь прямоугольного треугольника через гипотенузу и острый угол

Формула для нахождения площади прямоугольного треугольника по гипотенузе и острому углу:
Площадь прямоугольного треугольника через катет и прилежащий угол

Формула для нахождения площади прямоугольного треугольника по катету и прилежащему углу:
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу

Формула для нахождения площади прямоугольного треугольника по радиусу вписанной окружности и гипотенузе:
Площадь прямоугольного треугольника через вписанную окружность

Формула для нахождения площади прямоугольного треугольника по вписанной окружности:
Площадь прямоугольного треугольника по формуле Герона

Формула Герона для прямоугольного треугольника выглядит так:
Площадь равнобедренного треугольника
Площадь равнобедренного треугольника через основание и сторону

Формула площади равнобедренного треугольника через основание и сторону:
Площадь равнобедренного треугольника через основание и угол

Формула площади равнобедренного треугольника через основание и угол:
Площадь равнобедренного треугольника через основание и высоту

Формула площади равнобедренного треугольника через основание и высоту:
Площадь равнобедренного треугольника через боковые стороны и угол между ними

Формула площади равнобедренного треугольника через боковые стороны и угол между ними:
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами

Формула площади равнобедренного треугольника через основание и угол между боковыми сторонами:
Площадь равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности

Формула площади равностороннего треугольника через радиус описанной окружности:
Площадь равностороннего треугольника через радиус вписанной окружности

Формула площади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через сторону

Формула площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту

Формула площади равностороннего треугольника через высоту:
Площадь треугольника
Определение площади треугольника
Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.
Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.
Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.
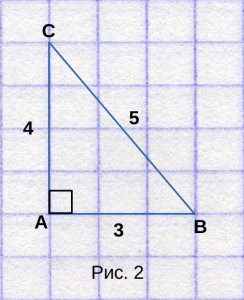
Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.
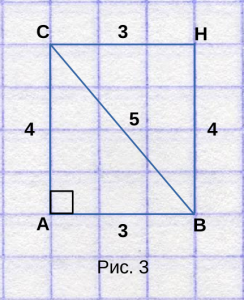
Как видим, весь прямоугольник занимает 12 полных клеток.
Формула площади прямоугольника равна произведению
одной стороны на другую — ( S = ab ) ,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.
Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: ( S = frac<1>2 ab ) .
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.
Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.
Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.
Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.
Формулы площади треугольника
Ⅰ. Через высоту и основание
a — сторона, на которую падает высота,
b — высота.
Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.
Ⅱ. Через все стороны и периметр
p — полупериметр, вычисляется по формуле: ( p = frac
a, b, c — стороны треугольника.
Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.
Эту формулу площади также называют формулой Герона.
Ⅲ. Через две стороны и угол между ними
[ S = frac<1> <2>a cdot b cdot sin β ]
a, b — стороны между которыми расположен угол β,
sin β — синус угла β.
Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.
Ⅳ. Через периметр и радиус вписанной окружности
[ S = r cdot frac
2 ]
r — радиус вписанной окружности,
P — периметр треугольника.
Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.
Ⅴ. Через все стороны и радиус описанной окружности
abc — произведение всех сторон треугольника,
R — радиус описанной окружности.
Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.
Ⅵ. Через сторону и два прилежащих к ней угла
a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.
Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.
Площадь треугольника через радиус описанной окружности — формулы и примеры определения
Одна из самых часто встречающихся в задачах по геометрии фигур — это треугольник. О его свойствах математики знают все. Основными из характеристик фигуры являются периметр и площадь. Их можно рассчитать, если известны некоторые элементы, например, углы и стороны. Определение площади треугольника через радиус описанной окружности не является тривиальной задачей, поэтому требует подробного рассмотрения.

Фигура с тремя сторонами
Чтобы понять, как рассчитывать площадь треугольника, вписанного в окружность, необходимо иметь четкое представление о рассматриваемой фигуре. Каждый школьник знает о геометрическом объекте, который ограничен тремя отрезками. Основными элементами треугольника являются следующие:

Помимо вершин и сторон, треугольник характеризуется дополнительными отрезками, которые часто используются для доказательства теорем и решения геометрических задач. К имеющим специальное название отрезкам относятся такие:

Вписанный в окружность треугольник
Чтобы уметь вычислять площадь описанного треугольника, следует понимать, о каком взаимном расположении многоугольника и окружности идет речь. Согласно определению, если через все вершины полигона проходит окружность, значит, он считается вписанным в нее. Это простое определение не всегда выполняется для произвольного многоугольника, однако, для любой правильной фигуры оно будет справедливым, например, для квадрата или прямоугольника.
Касательно треугольника следует отметить, что он является единственным многоугольником, для которого всегда можно найти центр и радиус описывающей его окружности. Причем независимо от того, какой тип фигуры рассматривается.

Пересечение медиатрис
В рассматриваемой фигуре имеется три разных медиатрисы. Каждую из них построить несложно для любой из сторон. Для построения следует выполнить последовательность действий:

Из проделанных построений следует один важный факт для всех треугольников: точка пересечения их медиатрис является центром описывающей фигуру окружности. Доказать это утверждение легко. Например, имеется треугольник ABC. Пусть проведена медиатриса m к стороне AB. Любая из точек, принадлежащих прямой m, находится на одинаковом расстоянии от вершин A и B.
Пусть проведена еще одна медиатриса n к стороне BC. Прямые m и n пересекаются в точке O. Поскольку O принадлежит обеим медиатрисам, то она, с одной стороны, находится на одном расстоянии от A и B, с другой стороны, она находится на одинаковой дистанции от вершин B и C. Этот факт дает право сделать вывод о том, что расстояния OA, OB и OC равны. Если их обозначить буквой R, то можно говорить, что R — радиус окружности с центром в точке O, которая проходит через три вершины треугольника, то есть описывается его.
Очевидно, что третья медиатриса также пройдет через O. В противном случае будут существовать три разные точки, которые одновременно будут находиться на одинаковом расстоянии от трех вершин треугольника и будут лежать в одной плоскости с ним, а это невозможно из свойств двумерного пространства.
Типы фигур и точка O
Поскольку для треугольника любого типа можно провести описывающую его окружность, то представляет интерес рассмотреть вопрос положения ее центра O. В общем случае существуют три типа рассматриваемого многоугольника:

Очевидно, что если треугольник является полностью вырожденным, то провести описывающую его окружность нельзя, поскольку такая фигура обращается в прямой отрезок.
Формулы для определения площади
Как известно, площадь треугольника произвольного типа может быть рассчитана, как половина произведения высоты h на длину основания a: S = ½*h*a. Существует также еще одно универсальное выражение для определения S — это половина модуля векторного произведения направляющих отрезков, образующих любые две стороны.
Что касается формул площади треугольника, описанного около окружности, то нужно отметить, что известны несколько из них. Соответствующие равенства имеют следующий вид:

- S = a*b*c/(4*R);
- S = (½*R*ha*hb*hc)^0,5;
- S = 2*R 2 *ha*hb*hc/(a*b*c).
Где a, b, c — длины соответствующих сторон треугольника, ha, hb, hc — высоты, проведенные к a, b и c, соответственно. Видно, что все три формулы требуют знание минимум 4 параметров для рассматриваемой фигуры (радиус и три высоты или три длины сторон).
Полезно также привести формулу для расчета радиуса R:
Здесь p = (a+b+c)/2 — полупериметр треугольника. Следует отметить, что знаменатель в выражении для радиуса является не чем иным, как формулой Герона для расчета площади S фигуры.
Решение задач
Как правило, прямое использование формул площади треугольника через окружность описанную является невозможным для типичных геометрических задач. Для их решения необходимо внимательно проанализировать условие и использовать все имеющиеся знания для определения неизвестных в выражениях для S через R.
Для некоторых задач может потребоваться использование уравнений прямых, которые на плоскости в векторной форме имеют вид:

(x, y) = (x0, y0) + α*(v1, v2).
Здесь (x, y) и (x0, y0) — координаты произвольной и известной точек прямой, соответственно, (v1, v2) — координаты направляющего вектора, α — числовой параметр.
Для закрепления полученных знаний полезно решить одну простую задачу. Известно, что один из острых углов в прямоугольном треугольнике составляет 30 °. Чему равна площадь этой фигуры, если радиус описанной окружности для нее составляет 12 см.
Для решения задачи воспользуемся следующим выражением через радиус окружности, описанной около треугольника, для площади:
Пусть c — это гипотенуза, тогда c = 2*R = 24 см. Катеты a и b можно связать с гипотенузой функциями синуса и косинуса:
- a = c*cos (α) = 24*3 0,5 /2 = 20,7846 см;
- b = c*sin (α) = 24*½ = 12 см.

Подставляя полученные значения в формулу для S через R, можно получить ответ:
S = a*b*c/(4*R) = 20,7846*12*24/(4*12) ≈ 124,71 см 2 .
Важно понимать, что формулы расчета площади рассматриваемого многоугольника через радиус описанной окружности используются редко, поскольку они могут быть заменены аналогичными более простыми выражениями, как в случае с высотой и основанием. В решенной задаче, например, можно было не применять указанную для S формулу, а просто рассчитать полупроизведение катетов:
S = ½*a*b = ½*20,7846*12 ≈ 124,71 см 2 .
Таким образом, вокруг каждого треугольника можно описать окружность радиуса R, центр которой расположен в точке пересечения его серединных перпендикуляров (медиатрис). Существует несколько формул для вычисления площади фигуры через радиус R, однако, все они требуют знания либо сторон, либо высот треугольника, и в большинстве случаев могут быть заменены более простыми выражениями при решении задач.
Площадь треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
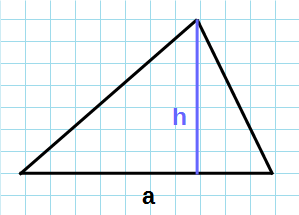
Площадь треугольника по основанию и высоте
Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом “высота” понимают высоту треугольника, проведенную к основанию (Рис.1):
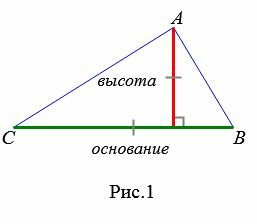 |
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.
Доказательство. Пусть AC основание треугольника ABC (Рис.2).
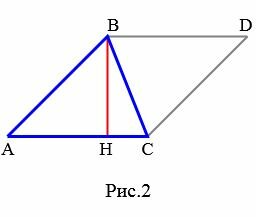 |
Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что
Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку ( small AC || BD ) и ( small AB || CD ), то ABDC является параллелограммой и, следовательно, ( small AC = BD ), ( small AB = CD . ) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна ( small S_
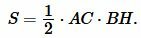  |
Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.
Доказательство. Пусть площадь треугольников ABC и A1B1C1 равны:
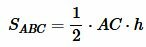 , , |
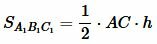 , , |
где AC и A1C1 основания треугольников ABC и A1B1C1, соответственно, а h их высоты.
Обозначим через k отношение
| ( small k= frac |
То есть отношение площадей треугольников с равными высотами равно отношению их оснований.
Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.
Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.
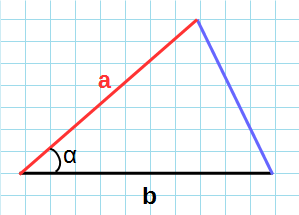
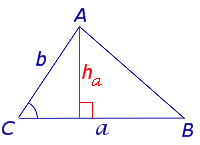
Площадь треугольника по двум сторонам и углу между ними
Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что
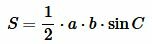 . . |
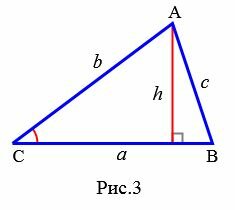 |
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):
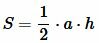 , , |
(1) |
где h − высота треугольника.
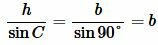 , , |
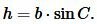 |
(2) |
Подставляя (2) в (1), получим:
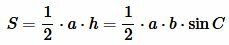 |
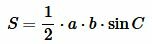  |
(3) |
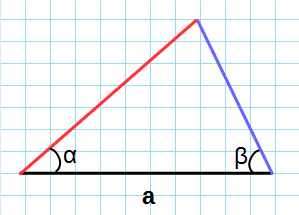
Площадь треугольника по стороне и прилежащим двум углам
Пусть известна сторона треугольника и две прилежащие углы (Рис.4).
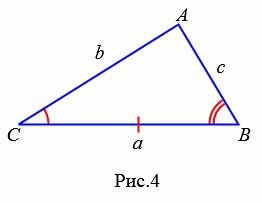 |
Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:
 |
(4) |
Найдем сторону b используя теорему синусов:
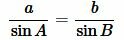 , , |
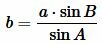 . . |
(5) |
В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:
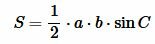 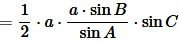 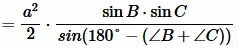 . . |
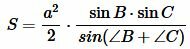 . . |
(6) |
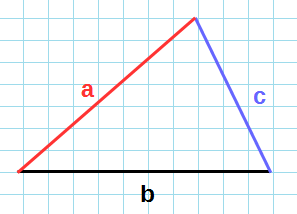
Площадь треугольника по трем сторонам. Формула Герона
Для нахождения площади треугольника по трем сторонам используют формулу Герона:
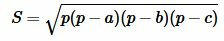 , , |
(7) |
где a, b, c − стороны треугольника, а p − полупериод треугольника:
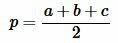 . . |
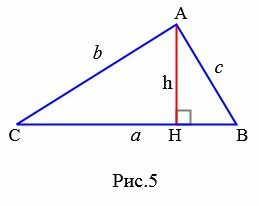 |
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:
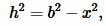 |
(8) |
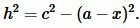 |
(9) |
Из (8) и (9) следует:
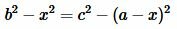 |
Откуда находим x:
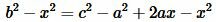 , , |
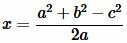 |
(10) |
Подставляя (10) в (8) найдем h:
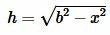 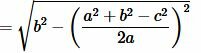 |
(11) |
Тогда площадь треугольника равна:
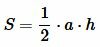 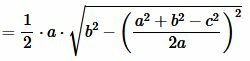 |
(12) |
Преобразовав (12) получим формулу (7):
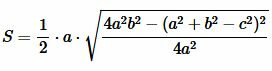 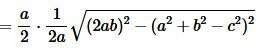 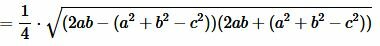 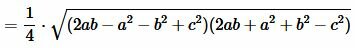 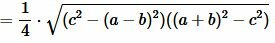 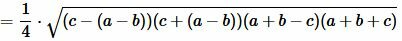 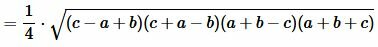 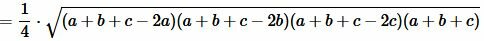 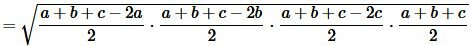 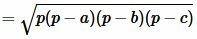 . . |
Площадь треугольника по трем сторонам и радусу описанной окружности
Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: ( small S=frac






