Монотонность функции – свойства, признаки и примеры решений

Монотонность функции – свойства, признаки и примеры решений

Пусть (y = fleft( x right)) является дифференцируемой функцией на интервале (left( right).) Функция называется возрастающей (или неубывающей ) на данном интервале, если для любых точек (, in left( right),) таких, что ( строго возрастающей на интервале (left( right).)

Аналогично определяются убывающая (или невозрастающая ) и строго убывающая функции.

Введенные понятия можно сформулировать в более компактной форме. Функция (y = fleft( x right)) называется

возрастающей ( неубывающей ) на интервале (left( right),) если [ , in left( right):;><строго возрастающей на интервале (left( right),) если [ , in left( right):;><убывающей ( невозрастающей ) на интервале (left( right),) если [ , in left( right):;><строго убывающей на интервале (left( right),) если [ , in left( right):;><Рис.1

Если функция (fleft( x right)) дифференцируема на интервале (left( right)) и принадлежит к одному из четырех рассмотренных типов (т.е. является возрастающей, строго возрастающей, убывающей или строго убывающей), то такая функция называется монотонной на данном интервале.

Понятия возрастания и убывания функции можно определить также и для отдельной точки (.) В этом случае рассматривается малая (delta)-окрестность (left( <– delta , + delta > right)) этой точки. Функция (y = fleft( x right)) является строго возрастающей в точке (,) если существует число (delta > 0,) такое, что [forall;x in left( <– delta ,> right) Rightarrow fleft( x right) fleft( <> right).] Аналогичным образом определяется строгое убывание функции (y = fleft( x right)) в точке (.)

Снова рассмотрим функцию (y = fleft( x right),) считая ее дифференцируемой на некотором интервале (left( right).) Возрастание или убывание функции на интервале определяется по знаку первой производной функции.

Теорема 1 .
Для того, чтобы функция (y = fleft( x right)) была возрастающей на интервале (left( right),) необходимо и достаточно, чтобы первая производная функции была неотрицательной всюду на данном интервале: [f’left( x right) ge 0;forall;x in left( right).] Аналогичный критерий действует для случая функции, убывающей на интервале (left( right):) [f’left( x right) le 0;forall;x in left( right).] Докажем обе части теоремы (необходимость и достаточность) для случая возрастающей функции.

Поскольку (f’left( c right) ge 0,) то правая часть равенства неотрицательна. Следовательно, [fleft( <> right) ge fleft( <> right).] т.е. функция (y = fleft( x right)) является возрастающей на интервале (left( right).)

Рассмотрим теперь случаи строгого возрастания и строгого убывания функции. Здесь существует похожая теорема, описывающая необходимые и достаточные условия. Опуская доказательство, сформулируем ее для случая строго возрастающей функции.

Теорема 2 .
Для того, чтобы дифференцируемая на интервале (left( right)) функция была строго возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялись следующие условия:

(f’left( x right) ge 0;forall;x in left( right);)

Производная (f’left( x right)) тождественно не равна нулю ни в каком промежутке (left[ <,> right] in left( right).)

Условие (1) содержится в теореме (1) и является признаком неубывающей функции. Дополнительное условие (2) требуется для того, чтобы исключить участки постоянства функции, в которых производная функции (fleft( x right)) тождественно равна нулю.

На практике (при нахождении интервалов монотонности) обычно используется достаточное условие строгого возрастания или строгого убывания функции. Из теоремы (2) следует такая формулировка достаточного признака:

Если для всех (x in left( right)) выполняется условие (f’left( x right) > 0) всюду в интервале (left( right),) кроме возможно лишь некоторых отдельных точек, в которых (f’left( x right) = 0,) то функция (fleft( x right)) является строго возрастающей .

Соответственно, условие (f’left( x right) строго убывающую функцию.

Число точек, в которых (f’left( x right) = 0,) является, как правило, конечным. Согласно теореме (2), они не могут плотно заполнять какой-либо промежуток в интервале (left( right).)

Приведем также признак строгого возрастания (убывания) функции в точке:

Если (f’left( <> right) > 0), то функция (fleft( x right)) строго возрастает в точке ();

Если (f’left( <> right) сумма функций (f + g) также возрастает (убывает) на этом интервале.

Если функция (f) возрастает (убывает) на интервале (left( right),) то противоположная функция (-f) убывает (возрастает) на этом интервале.

Если функция (f) возрастает (убывает) на интервале (left( right),) то обратная функция (largefrac<1>normalsize) убывает (возрастает) на этом интервале.

Если функции (f) и (g) возрастают (убывают) на интервале (left( right)) и, кроме того, (f ge 0), (g ge 0), то произведение функций (fg) также возрастает (убывает) на этом интервале.

Если функция (g) возрастает (убывает) на интервале (left( right),) а функция (f) возрастает (убывает) на интервале (left( right),) где (g:left( right) to left( right),) то композиция функций (f circ g) (т.е. сложная функция (y = fleft( right)) также возрастает (убывает) на интервале (left( right).)

Возьмем две произвольные точки () и (,) такие что [0 le lt .] Рассмотрим разность значений функции в этих точках: [ > right) – fleft( <> right) > = right) – left( right) > = = – > right)left( <+ > right).> ] В последнем выражении, очевидно, что ( <– > > 0) и ( <+ > > 0) (поскольку по условию рассматриваются неотрицательные значения (x)). В результате получаем: [ – > right)left( <+ > right) > 0,>;; > right) – fleft( <> right) > 0.> ] Это означает по определению, что функция (fleft( x right) = + 1) является строго возрастающей на заданном интервале.

Выберем две произвольные точки (<>) и (<>,) такие что ( формуле разности кубов , получаем: [ = – > right)left( + x_1^2> right).> ] Во второй скобке можно выделить полный квадрат: [ + x_1^2 > = cdot frac<<>> <2>+ frac<> <4>+ frac<<3x_2^2>> <4>> = <+ frac<<>><2>> right)^2> + frac<<3x_2^2>> <4>> 0.> ] Отсюда видно, что квадратичное выражение всегда положительно (оно равно нулю лишь при ( = = 0,) что противоречит условию ( 0,) если ( – > 0,) т.е. функция (fleft( x right) = ) является строго возрастающей.

Данная функция является суммой функций () и (3.)

Первую функцию () можно рассматривать как произведение двух одинаковых функций (). Из примера (1) следует, что квадратичная функция () строго возрастает при (x ge 0.) Следовательно, функция () также строго возрастает при (x ge 0) на основании свойства (4).

Второе слагаемое (3) представляет собой трехкратную сумму функций () и, поэтому, также является строго возрастающей (на основании свойства (1)).

Итак, исходная функция (fleft( x right) = + 3) является суммой двух строго возрастающих функций и, следовательно, также строго возрастает при (x ge 0.)

Для контроля рассмотрим также неравенство (f’left( x right) Рис.5

Таким образом, функция убывает (в строгом смысле) в интервалах (left( < - infty , - 1>right)) и (left( <1, infty>right)) и возрастает в промежутке (left( <-1, 1>right).) Учитывая, что корень функции равен (x = 0,) можно схематически нарисовать ее график (рисунок (6)).

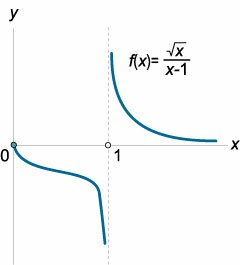
Следовательно, на основании достаточного признака монотонности, функция строго возрастает при (x in left( normalsize,infty > right)) и строго убывает при (x in left( <0, largefrac<1>normalsize> right).) Ее вид схематически приведен на рисунке (10).

На основании достаточного признака монотонности заключаем, что функция возрастает при (x in left( <0,largefrac<1><2>normalsize> right)) и убывает при (x in left( <2>normalsize,1> right).) График функции представляет собой полуокружность с центром в точке (left( <2>normalsize,0> right)) и радиусом (<2>normalsize>) (рисунок (14)).

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №15. Возрастание и убывание функции.

Перечень вопросов, рассматриваемых в теме

1) Нахождение промежутков монотонности функции,

2) Определение алгоритма нахождения промежутков возрастания и убывания функции,

3) Решение задачи на нахождения промежутков возрастания и убывания функции

Глоссарий по теме

Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)

1. Найти D(f)
2. Найти f‘(x).
3. Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х₁ и х₂ из этого промежутка из неравенства х₁ f(x₂)

1. Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
2. Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.

Примеры и разбор решения заданий тренировочного модуля

№1. Определите промежутки монотонности функции

у = -3х 3 + 4х 2 + х – 10.

1.Найдем область определения функции.

D(y) =

2.Найдем производную функции.

3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).

Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

Так как на интервале производная функции отрицательна, то на этом интервале функция убывает.

Так как на интервале производная функции положительна, то на этом интервале функция возрастает.

Так как на интервале производная функции отрицательна, то на этом интервале функция убывает.

Так как в точках функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.

Следовательно, функция возрастает на ; функция убывает на и на .

Ответ: Функция возрастает на

Функция убывает на и на .

№2. Определите промежутки монотонности функции

у = х 5 –5х 4 +5х 3 – 4.

y‘ =

1. Функция возрастает на ; функция убывает на .

Ответ: Функция возрастает на ;

функция убывает на .

Монотонность и экстремумы функции

Определение 1. Функция 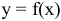называется возрастающей в интервале 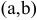, если большему значению аргумента 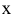из этого интервала соответствует и большее значение функции.

Определение 2. Функция 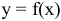называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Достаточное условие возрастания ( убывания ) функции:

Если во всех точках 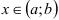выполняется неравенство 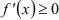(причем равенство 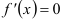выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция 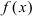возрастает в интервале .

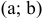Если в данном промежутке производная данной функции неотрицательна, то функция в этом промежутке убывает.

Справедливы и обратные утверждения.

Определение 3. Максимумом функции 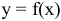такое ее значение 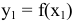, которое больше всех ее значений, принимаемых в точках 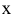, достаточно близких к точке 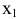и отличных от нее, т. 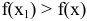е. , где 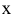— любая точка из интервала, содержащего точку 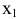( 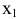— точка максимума ).

Определение 4. Минимумом функции 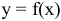называется такое ее значение 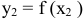, которое меньше всех других ее значений, принимаемых в точках 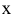, достаточно близких к точке 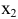и отличных от нее, т. 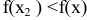е. , где 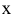— любая точка из некоторого интервала, содержащего точку 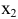( 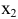— точка минимума).

Максимум или минимум функции называется экстремумом функции. Точки, в которых достигается экстремум, называются точками экстремума.

Функция может иметь экстремум в тех точках области определения, в которых производная равна нулю или не существует . Такие точки называются критическими .

Достаточное условие экстремума

Если в точке 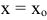производная функции 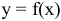обращается в нуль или не существует, и меняет знак при переходе через эту точку, то 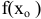— экстремум функции, причем:

1) функция имеет максимум в точке 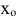, если знак производной меняется с «+» на «-»;

2) функция имеет минимум в точке 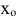, если знак производной меняется с «-» на «+»%

3) функция не имеет экстремума, если знак производной не меняется.

Алгоритм исследования непрерывной функции 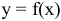на монотонность и экстремумы.

1. Найти область определения и производную .
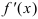2. Найти критические точки.
3. Отметить критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4. Опираясь на теоремы сделать выводы о монотонности и о ее точках экстремума.

Пример:

Исследовать функцию 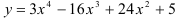на монотонность и экстремумы.

Решение:

1. Найдем область определения: 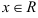и производную данной функции:

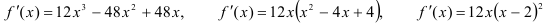
2. Найдем критические точки.

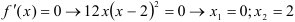— это две критические точки.

3. Отметим полученные точки на числовой прямой и схематически укажем знаки производной по промежуткам области определения.

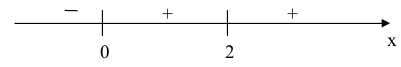
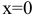— точка минимума функции, а 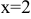точкой экстремума не является.

На промежутке 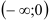функция убывает, а на промежутке 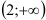функция возрастает.

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Монотонность функций

(blacktriangleright) Функция (f(x)) называется возрастающей на промежутке (X) , если для любых (x_1, x_2in X) , таких что (x_1 , выполнено (f(x_1) .

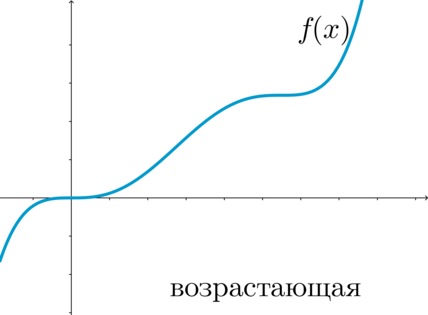
Функция называется неубывающей на промежутке (X) , если для любых (x_1, x_2in X) , таких что (x_1 , выполнено (f(x_1)leq f(x_2)) .

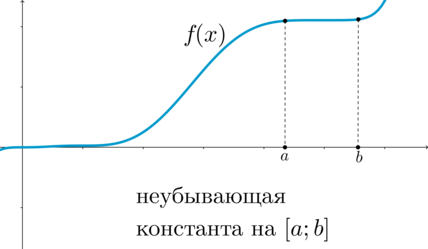
(blacktriangleright) Функция (f(x)) называется убывающей на промежутке (X) , если для любых (x_1, x_2in X) , таких что (x_1 , выполнено (f(x_1)>f(x_2)) .

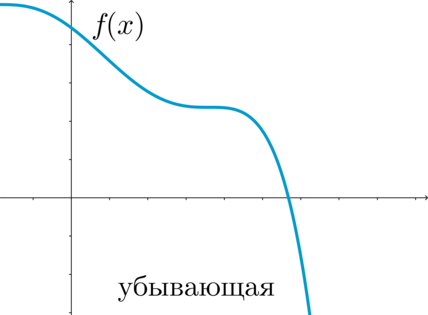
Функция называется невозрастающей на промежутке (X) , если для любых (x_1, x_2in X) , таких что (x_1 , выполнено (f(x_1)geq f(x_2)) .

(blacktriangleright) Возрастающие и убывающие функции называют строго монотонными, а невозрастающие и неубывающие — просто монотонными.

(blacktriangleright) Основные свойства:

I. Если функция (f(x)) — строго монотонна на (X) , то из равенства (x_1=x_2) ( (x_1,x_2in X) ) следует (f(x_1)=f(x_2)) , и наоборот.

Пример: функция (f(x)=sqrt x) является строго возрастающей при всех (xin [0;+infty)) , поэтому из равенства (sqrt x=sqrt 4) следует (x=4) .

II. Если функция (f(x)) — строго монотонна на (X) , то уравнение (f(x)=c) , где (c) — некоторое число, всегда имеет не более одного решения на (X) .

Пример: функция (f(x)=x^2) является строго убывающей при всех (xin (-infty;0]) , поэтому уравнение (x^2=9) имеет на этом промежутке не более одного решения, а точнее одно: (x=-3) .

функция (f(x)=-dfrac 1) является строго возрастающей при всех (xin (-1;+infty)) , поэтому уравнение (-dfrac 1=0) имеет на этом промежутке не более одного решения, а точнее ни одного, т.к. числитель левой части никогда не может быть равен нулю.

III. Если функция (f(x)) — неубывает (невозрастает) и непрерывна на отрезке ([a;b]) , причем на концах отрезка она принимает значения (f(a)=A, f(b)=B) , то при (Cin [A;B]) ( (Cin [B;A]) ) уравнение (f(x)=C) всегда имеет хотя бы одно решение.

Пример: функция (f(x)=x^3) является строго возрастающей (то есть строго монотонной) и непрерывной при всех (xinmathbb) , поэтому при любом (Cin (-infty;+infty)) уравнение (x^3=C) имеет ровно одно решение: (x=sqrt[3]) .

Найдите все значения параметра (a) , при каждом из которых уравнение [27x^6+(a-x)^3+3x^2=x-a]

имеет ровно два корня.

Перепишем уравнение в виде: [(3x^2)^3+3x^2=(x-a)^3+(x-a)] Рассмотрим функцию (f(t)=t^3+t) . Тогда уравнение перепишется в виде: [f(3x^2)=f(x-a)] Исследуем функцию (f(t)) . [f'(t)=3t^2+1>0] Следовательно, функция (f(t)) возрастает при всех (t) . Значит, каждому значению функции (f(t)) соответствует ровно одно значение аргумента (t) . Следовательно, для того, чтобы уравнение имело корни, нужно: [3x^2=x-a quadLeftrightarrowquad 3x^2-x+a=0] Чтобы полученное уравнение имело два корня, нужно, чтобы его дискриминант был положительным: [D=1-12a>0 quadRightarrowquad a

Найдите все значения параметра (a) , при которых уравнение [7^-7^=sqrt[7]<2x-ax^2>-sqrt[7]<1-x^2>]

имеет два корня.

(Задача от подписчиков.)

Сделаем замену: (ax^2-2x=t) , (x^2-1=u) . Тогда уравнение примет вид: [7^t-7^u=sqrt[7]<-t>-sqrt[7] <-u>quadLeftrightarrowquad 7^t+sqrt[7]t=7^u+sqrt[7]u] Рассмотрим функцию (f(w)=7^w+sqrt[7]w) . Тогда наше уравнение примет вид: [f(t)=f(u).]

Найдем производную [f'(w)=7^wln7+dfrac1<7cdot sqrt[7]>.] Заметим, что при всех (wne 0) производная (f'(w)>0) , т.к. (7^w>0) , (w^6>0) . Заметим также, что сама функция (f(w)) определена при всех (w) . Т.к. к тому же (f(w)) непрерывна, то мы можем сделать вывод, что (f(w)) возрастает на всем (mathbb) .
Значит, равенство (f(t)=f(u)) возможно тогда и только тогда, когда (t=u) . Вернемся к изначальным переменным и решим полученное уравнение:

[ax^2-2x=x^2-1quadLeftrightarrowquad (a-1)x^2-2x+1=0] Для того, чтобы данное уравнение имело два корня, оно должно быть квадратным и его дискриминант должен быть положительным:

[begin a-1ne 0\ 4-4(a-1)>0end quadLeftrightarrowquad beginane1\a

Найдите все положительные значения параметра (a) , при которых уравнение

имеет как минимум (2) решения.

Перенесем все слагаемые, содержащие (ax) , влево, а содержащие (x^2) – вправо, и рассмотрим функцию
[f(t)=5(t-2)^3+15e^t+6e^tcdot sin <2t>+3e^tcdot cos<2t>]

Тогда исходное уравнение примет вид:
[f(ax)=f(x^2)]

Найдем производную:
[f'(t)=15(t-2)^2+15e^tcdot (1+cos<2t>)]

Т.к. ((t-2)^2 geqslant 0, e^t>0, 1+cos <2t>geqslant 0) , то (f'(t)geqslant 0) при любых (tin mathbb) .

Причем (f'(t)=0) , если ((t-2)^2=0) и (1+cos<2t>=0) одновременно, что не выполняется ни при каких (t) . Следовательно, (f'(t)> 0) при любых (tin mathbb) .

Таким образом, функция (f(t)) строго возрастает при всех (tin mathbb) .

Значит, уравнение (f(ax)=f(x^2)) равносильно уравнению (ax=x^2) .

Уравнение (x^2-ax=0) при (a=0) имеет один корень (x=0) , а при (ane 0) имеет два различных корня (x_1=0) и (x_2=a) .
Нам нужно найти значения (a) , при которых уравнение будет иметь не менее двух корней, учитывая также то, что (a>0) .
Следовательно, ответ: (ain (0;+infty)) .

Найдите все значения параметра (a) , при каждом из которых уравнение [2^>cdot log_<3>>>+log_9<(sqrt+2)>=0]

имеет единственное решение.

Рассмотрим функцию (y=2^tcdot log_<9>><(t+2)>) при (tgeqslant 0) (т.к. (sqrtgeqslant 0) ).

Производная (y’=left( -2^tcdot log_9<(t+2)>right)’=-dfrac<2^t>cdot left( ln 2cdot ln<(t+2)>+dfrac<1>right)) .

Т.к. (2^t>0, dfrac<1>>0, ln<(t+2)>>0) при всех (tgeqslant 0) , то (y’ при всех (tgeqslant 0) .

Следовательно, при (tgeqslant 0) функция (y) монотонно убывает.

Уравнение можно рассматривать в виде (y(t)=y(z)) , где (z=ax, t=sqrt) . Из монотонности функции следует, что равенство возможно только в том случае, если (t=z) .

Значит, уравнение равносильно уравнению: (ax=sqrt) , которое в свою очередь равносильно системе: [begin a^2x^2-x-1=0\ ax geqslant 0 end]

При (a=0) система имеет одно решение (x=-1) , которое удовлетворяет условию (axgeqslant 0) .

Рассмотрим случай (ane 0) . Дискриминант первого уравнения системы (D=1+4a^2>0) при всех (a) . Следовательно, уравнение всегда имеет два корня (x_1) и (x_2) , причем они разных знаков (т.к. по теореме Виета (x_1cdot x_2=-dfrac<1> ).

Это значит, что при (a условию (axgeqslant 0) подходит отрицательный корень, при (a>0) условию подходит положительный корень. Следовательно, система всегда имеет единственное решение.

Значит, (ain mathbb) .

Найдите все значения параметра (a) , при каждом из которых уравнение [2x^3-3x(ax+x-a^2-1)-3a-a^3=0]

имеет хотя бы один корень из отрезка ([-1;0]) .

Рассмотрим функцию (f(x)=2x^3-3x(ax+x-a^2-1)-3a-a^3) при некотором фиксированном (a) . Найдем ее производную: (f'(x)=6x^2-6ax-6x+3a^2+3=3(x^2-2ax+a^2+x^2-2x+1)=3((x-a)^2+(x-1)^2)) .

Заметим, что (f'(x)geqslant 0) при всех значениях (x) и (a) , причем равна (0) только при (x=a=1) . Но при (a=1) :
(f'(x)=6(x-1)^2 Rightarrow f(x)=2(x-1)^3 Rightarrow) уравнение (2(x-1)^3=0) имеет единственный корень (x=1) , не удовлетворяющий условию. Следовательно, (a) не может быть равно (1) .

Значит, при всех (ane 1) функция (f(x)) является строго возрастающей, следовательно, уравнение (f(x)=0) может иметь не более одного корня. Учитывая свойства кубической функции, график (f(x)) при некотором фиксированном (a) будет выглядеть следующим образом:

Значит, для того, чтобы уравнение имело корень из отрезка ([-1;0]) , необходимо: [begin f(0)geqslant 0\ f(-1)leqslant 0 end Rightarrow begin a(a^2+3)leqslant 0\ (a+2)(a^2+a+4)geqslant 0 end Rightarrow begin aleqslant 0\ ageqslant -2 end Rightarrow -2leqslant aleqslant 0]

Таким образом, (ain [-2;0]) .

Найдите все значения параметра (a) , при каждом из которых уравнение [(sin^2x-5sin x-2a(sin x-3)+6)cdot (sqrt2a+8xsqrt<2x-2x^2>)=0]

(Задача от подписчиков)

ОДЗ уравнения: (2x-2x^2geqslant 0 quadLeftrightarrowquad xin [0;1]) . Следовательно, для того, чтобы уравнение имело корни, нужно, чтобы хотя бы одно из уравнений [sin^2x-5sin x-2a(sin x-3)+6=0 quad >>quad sqrt2a+8xsqrt<2x-2x^2>=0] имело решения на ОДЗ.

1) Рассмотрим первое уравнение [sin^2x-5sin x-2a(sin x-3)+6=0 quadLeftrightarrowquad left[begin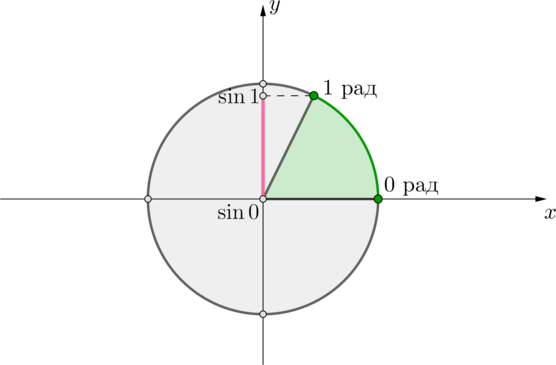begin &sin x=2a+2\ &sin x=3\ end endright. quadLeftrightarrowquad sin x=2a+2] Данное уравнение должно иметь корни на ([0;1]) . Рассмотрим окружность:

Таким образом, мы видим, что для любых (2a+2in [sin 0;sin 1]) уравнение будет иметь одно решение, а для всех остальных – не будет иметь решений. Следовательно, при (ain left[-1;-1+0,5sin 1right]) уравнение имеет решения.

2) Рассмотрим второе уравнение [sqrt2a+8xsqrt<2x-2x^2>=0 quadLeftrightarrowquad 8xsqrt=-a]

Рассмотрим функцию (f(x)=8xsqrt) . Найдем ее производную: [f'(x)=-4cdot dfrac>] На ОДЗ производная имеет один ноль: (x=frac34) , который к тому же является точкой максимума функции (f(x)) .
Заметим, что (f(0)=f(1)=0) . Значит, схематично график (f(x)) выглядит так: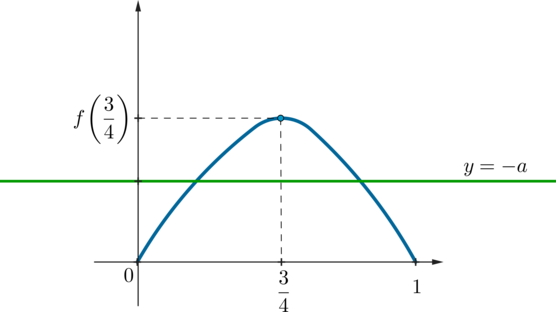

Следовательно, для того, чтобы уравнение имело решения, нужно, чтобы график (f(x)) пересекался с прямой (y=-a) (на рисунке изображен один из подходящих вариантов). То есть нужно, чтобы [0leqslant -aleqslant fleft(dfrac34right) quadRightarrowquad -dfrac<3sqrt3>2leqslant aleqslant 0]

3) Таким образом, изначальное уравнение будет иметь решения при (ain left[-1;-1+0,5sin 1right]) или (ain left[-dfrac<3sqrt3>2;0right]) . Объединяя эти решения, получим [ain left[-dfrac<3sqrt3>2;0right].]

Найдите все значения параметра (a) , при каждом из которых уравнение [sqrt+5x^2-9x+3a+8=dfrac]

имеет ровно одно решение.

Рассмотрим семейства функций (f_a(x)=sqrt+5x^2-9x+3a+8, g_a(x)=dfrac) .

ОДЗ уравнения: (xgeqslant 1) . При этих (x) :

Функция (y_1=sqrt) является строго возрастающей. Графиком функции (y_2=5x^2-9x) является парабола, вершина которой находится в точке (x=dfrac<9><10>) . Следовательно, при всех (xgeqslant 1) функция (y_2) также строго возрастает (правая ветвь параболы). Т.к. сумма строго возрастающих функций есть строго возрастающая, то (f_a(x)) – строго возрастает (константа (3a+8) не влияет на монотонность функции).

Функция (g_a(x)=dfrac) при всех (xgeqslant 1) представляет собой часть правой ветви гиперболы и является строго убывающей.

Решить уравнение (f_a(x)=g_a(x)) — значит найти точки пересечения функций (f) и (g) . Из их противоположной монотонности следует, что уравнение может иметь не более одного корня.

При (xgeqslant 1) (f_a(x)geqslant 3a+4, 0 . Следовательно, уравнение будет иметь единственное решение в том случае, если:

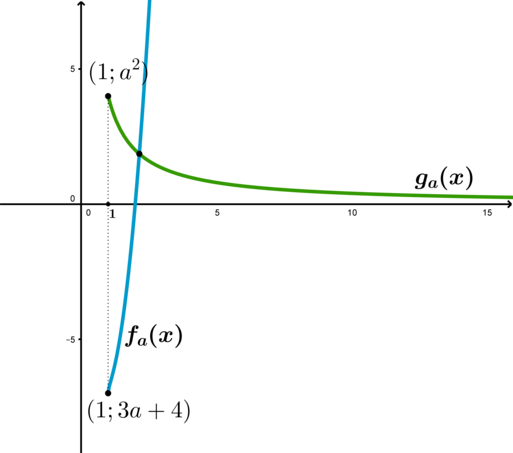
[3a+4leqslant a^2 Rightarrow ain (-infty;-1]cup[4;+infty)]

Подготовка к Единому государственному экзамену по математике зачастую вызывает особые затруднения у выпускников. Есть множество сложных заданий, которым уделяется недостаточно внимания в общеобразовательной программе. В их числе нахождение интервалов монотонности функций и точек экстремума. Как показывает практика последних лет, многие выпускники сталкиваются с проблемами в решении подобных заданий. Поэтому стоит сделать акцент на их повторении, чтобы легко справляться даже с задачами повышенного уровня сложности. В этом вам поможет наш онлайн-сервис.

Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха!

Наш образовательный портал позволит вам быстро и эффективно подготовиться к предстоящему итоговому тестированию по математике. Наши преподаватели собрали, систематизировали и оформили информацию по тематике в максимально простой и понятной форме. Поэтому ученики смогут быстро воспринимать материалы. Благодаря особому методу они уже через несколько дней будут решать даже те задания, которые казались невыполнимыми.

Начните с повторения правил и формул, которые могут понадобиться при исследовании монотонности функций. Для этого перейдите в раздел «Теоретическая справка». Вы вспомните виды и свойства функций, как определить знак производной, найти критические точки и многое другое. В каталогах представлены как типовые примеры по тематике, так и задания повышенного уровня сложности, которые могут встретиться в ЕГЭ. Их список постоянно обновляется и дополняется, поэтому выпускники будут ежедневно получать новые задания без повторений. Дети научатся находить количество значений необходимых параметров, работать с различными видами тригонометрических функций, а также справляться с уравнениями, в которых встречаются корни различной степени и логарифмы.

Если у школьника возникнут сложности с решением примера, он может добавить задание в «Избранное» и вернуться к нему позже.

Для того чтобы занятия проходили максимально результативно, советуем начать с самых простых заданий, где нужно указать промежутки монотонности функций y=f(x), и постепенно переходить к более трудным. Так ученики смогут выявить свои самые слабые стороны и сделать упор на решении конкретных типов упражнений.

Чтобы получить большие результаты, рекомендуем обращаться к нашему порталу ежедневно. Начните подготовку к итоговому тестированию уже сегодня вместе с онлайн-сервисом «Школково»!

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

теория по математике функции

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

График функции у=k/x выглядит следующим образом: 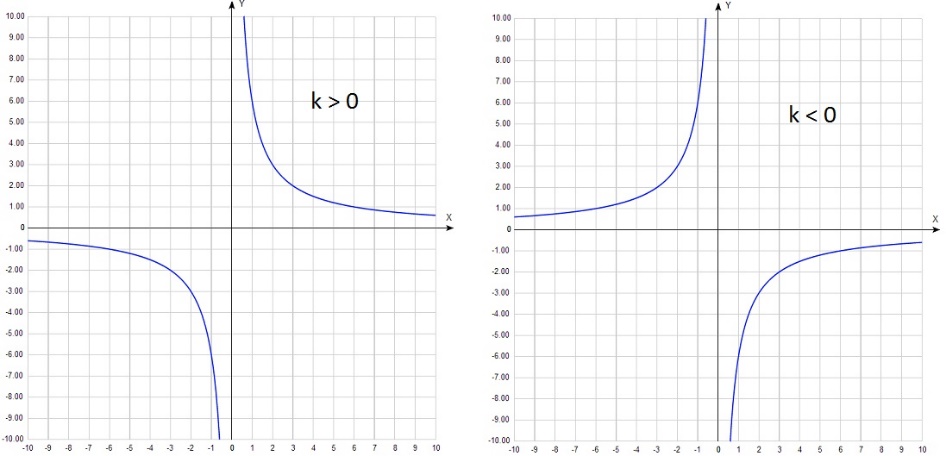По данному рисунку видно, что нулей функции не существует. Как найти нули функции?

1. Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
2. Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.

Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.

в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.

На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.

Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Возрастание и убывание функции

Общие понятия о поведении функций

Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.

Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.

Соответственно, монотонная функция может быть возрастающая или убывающая.

Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.

Математическое выражение этого определения выглядит следующим образом:

Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.

Математическое выражение этого определения выглядит следующим образом:

Разберем примеры решения задач на изучение характера поведения функции.

Задача 1. Задана функция (y=x^3+1) . Исследовать ее характер в интервале ([0;2]) .
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
(y_1=0^3+1=1) ;
(y_2=2^3+1=9) .

Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.

Задача 2 . Задана функция (y=<1over x>) . Определить ее характер в интервале ([1;2]) .
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
(y_1=<1over 1>=1) ;
(y_2=<1over2>=0.5) .

Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.

Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.

Не нашли что искали?

Просто напиши и мы поможем

Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.

Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.

Разберем задачу на исследование характера поведения функции. При данной функции (y=5) исследовать ее характер в интервале ([0;2]) .

По сути эту функцию можно записать как (y=5+0∙x) , подставляя крайние значения отрезка, получим:
(y_1=5+0∙0=5) ;
(y_2=5+0∙2=5) .

То есть функция (y=5) будет постоянной.

Постоянная, не убывающая и не возрастающая функции не есть монотонные.

Свойства монотонных функций

К свойствам монотонных функций относятся такие характеристики:

• если две или больше возрастающих функций суммируются, то в результате получается тоже возрастающая функция;
• результатом произведения положительных возрастающих функций будет возрастающая функция;
• при композиции двух возрастающих функций получается также функция, которая будет возрастать;
• при положительной функции (f(x)) , функция (f^n (x)) тоже будет возрастать, при условии, что (n) является натуральным числом;
• при сохранении возрастающей функцией (f(x)) своего знака, обратная ей функция будет убывать;
• при возрастающей функции (f(x)) и константе c справедливо, что функции (cf(x)) и (f(x)+c) , при (c>0) , будут возрастать.

Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:

Монотонность функций

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ f (x₂).

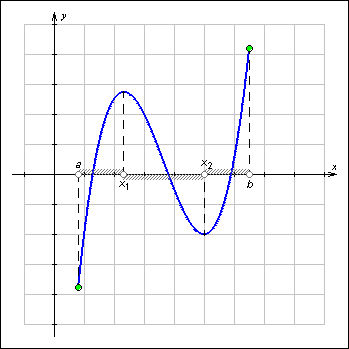Рисунок 1.3.5.1. Промежутки возрастания и убывания функции

На показанном на рисунке графике функция y = f (x), 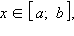возрастает на каждом из промежутков [a; x₁) и (x₂; b] и убывает на промежутке (x₁; x₂). Обратите внимание, что функция возрастает на каждом из промежутков [a; x₁) и (x₂; b], но не на объединении промежутков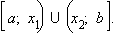

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ 0) и f + c также возрастают, а функция cf (cn также возрастает.

Аналогичные утверждения можно сформулировать и для убывающей функции.

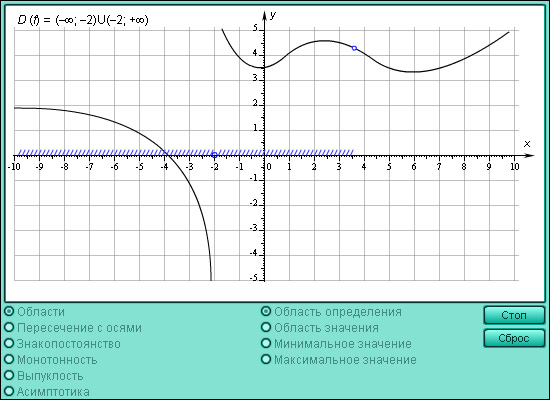Модель 1.9. Свойства функции

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

Если для любого 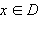(x ≠ a) выполняется неравенство f (x) ≤ f (a) 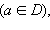то точка a называется точкой наибольшего значения функции на множестве D:

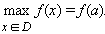Если для любого 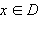(x ≠ b) выполняется неравенство f (x) > f (b) 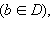то точка b называется точкой наименьшего значения функции на множестве D.

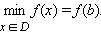Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

Наибольшее и наименьшее значения функции y=f(x) на [а,b].