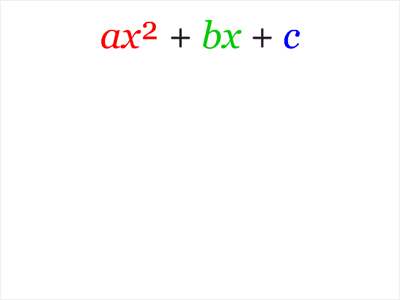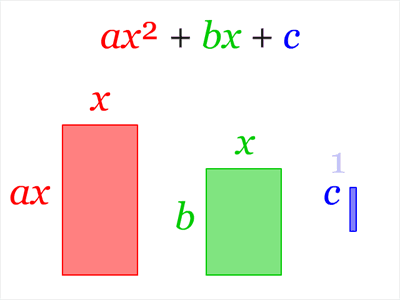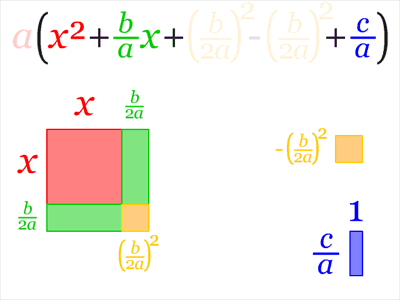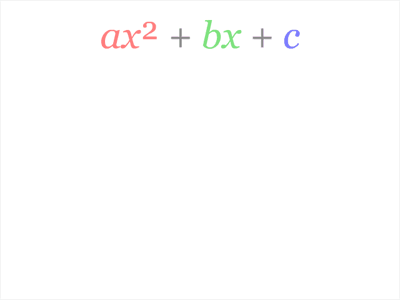ГДЗ по Алгебре
ГДЗ по алгебре – это сборники решенных примеров и задач с пояснениями от квалифицированных педагогов России. Решебники с подробными ответами научат находить корни уравнения и точки в системе координат, упрощать тождества и применять формулы сокращённого умножения. Готовые домашние задания помогут исправить ошибки, разобрать сложные примеры, подготовиться к контрольным.
- 7 класс
- 8 класс
- 9 класс
За 7 класс

Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013-2017г.

Издатель: А.Г. Мордкович и др., 2013-2019г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015-2018г.
За 8 класс

Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013-2017г.

Издатель: А.Г. Мордкович – Мнемозина, 2010-2013г.

Издатель: А.Г. Мерзляк – Вентана-Граф, 2013-2019г.
За 9 класс

Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2019г.

Издатель: А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина – 2010-2017г.

Издатель: А.Г. Мерзляк. Вентана-Граф, 2014-2021г.
Решебники по алгебре – неоценимая помощь школьникам
Алгебра изучает формулы и законы для упрощения числовых и буквенных выражений. Закономерности важно не только зазубрить, но понять их логику и научиться применять на практике. Решебники по алгебре с пояснениями помогают школьникам:
- проверить домашние упражнения;
- разобраться в алгоритмах решения примеров и задач;
- подготовиться к контрольным и экзаменам.
ГДЗ по алгебре с подробными ответами позволяют сэкономить время на выполнение домашней работы, исправить ошибки, научиться оформлять примеры и уравнения.
Родителям не придется искать репетиторов или тратить круглую сумму на дополнительные занятия. Теперь они самостоятельно смогут проверить решения своих детей.
ГДЗ по алгебре онлайн
Делать домашнюю работу нужно не только качественно, но и быстро. Можно усвоить материал и потратить на домашку всего 1-2 часа. Решебники по алгебре с пояснениями и теорией позволяют:
- найти задание по фамилии автора и номеру задания;
- открыть задачу с телефона, планшета, компьютера.
Бесплатно и без регистрации на сайте Ответкин.инфо доступны ГДЗ по алгебре в кратком варианте. Зарегистрированные пользователи могут 3 раза в сутки просматривать подробные ответы с теорией. Если лимита недостаточно, то пользователям доступны платные подписки.
Все подробные решения составляют квалифицированные педагоги российских школ. Готовые задания проходят многократную проверку, что исключает любые ошибки и неточности.
Алгебра
А́лгебра (от араб. الجبر , «аль-джабр» — восполнение [1] ) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.
Алгебра — это наука, изучающая алгебраические системы с точностью до изоморфизма.
Алгебраическая система — упорядоченная пара множеств  . Первое множество (
. Первое множество ( ) — элементы какой либо природы (числа, понятия, буквы). Второе множество (
) — элементы какой либо природы (числа, понятия, буквы). Второе множество ( ) — операции над первым множеством (сложение, умножение, возведение в степень). Примеры: группа, кольцо, поле.
) — операции над первым множеством (сложение, умножение, возведение в степень). Примеры: группа, кольцо, поле.
Содержание
История
Истоки алгебры уходят к временам глубокой древности. Ещё 4000 лет назад вавилонские учёные могли решать квадратные уравнения. Тогда никаких обозначений не было, и уравнения записывались в словесной форме. Первые обозначения появились в Древней Греции благодаря учёному Диофанту. Неизвестное число он назвал «ἀριθμός», вторую степень неизвестного — «δύναμις», третью «κύβος», четвёртую — «дюнамодюнамис», пятую — «дюнамокюбос», шестую — «кюбоккюбос». Все эти величины он обозначал сокращениями (ар, дю, кю, ддю, дкю, ккю). Ни вавилоняне, ни греки не знали и не признавали отрицательные числа.
За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения. Они уже знали отрицательные и иррациональные числа. Поскольку в китайском языке каждый символ обозначает понятие, то сокращений не было. В 13 веке китайцы открыли закон образования биномиальных коэффициентов, ныне известный как «треугольник Паскаля». В Европе он был открыт лишь 250 лет спустя. [2]
Как наука, алгебра стала существовать благодаря мусульманскому учёному из Средней Азии Аль-Хорезми. Впервые термин «алгебра» встретился в 825 году в сочинении этого учёного «Краткая книга об исчислении аль-джабра и аль-мукабалы». Слово «аль-джабр» при этом означало операцию переноса вычитаемых из одной части уравнения в другую и его буквальный смысл «восполнение» [1] .
В 12 веке алгебра попала в Европу. С этого времени начинается её бурное развитие. Были открыты способы решения уравнений 3 и 4 степеней. Распространения получили отрицательные и комплексные числа. Было доказано, что любое уравнение выше 4 степени нельзя решить алгебраическим способом.
Вплоть до второй половины XX века практическое применение алгебры ограничивалось, в основном, решением алгебраических уравнений и систем уравнений с несколькими переменными. Во второй половине XX века началось бурное развитие ряда новых отраслей техники. Появились электронно-вычислительные машины, устройства для хранения, переработки и передачи информации, системы наблюдения типа радара. Проектирование новых видов техники и их использование немыслимо без применения современной алгебры. Так, электронно-вычислительные машины устроены по принципу конечных автоматов. Для проектирования электронно-вычислительных машин и электронных схем используются методы булевой алгебры. Современные языки программирования для ЭВМ основаны на принципах теории алгоритмов. Теория множеств используется в системах компьютерного поиска и хранения информации. Теория категорий используется в задачах распознавания образов, определении семантики языков программирования, и других практических задачах. Кодирование и декодирование информации производится методами теории групп. Теория рекуррентных последовательностей используется в работе радаров. Экономические расчеты невозможны без использования теории графов. Математическое моделирование широко использует все разделы алгебры.
Классификация
Алгебру можно грубо разделить на следующие категории:
- Элементарная алгебра, которая изучает свойства операций с вещественными числами, где символами обозначаются постоянные и переменные, а также правила преобразования математических выражений и уравнений с использованием этих символов. Обычно преподаётся в школе под названием алгебра. Университетские курсы теории групп тоже можно назвать элементарной алгеброй.
- Абстрактная алгебра, иногда называемая современной алгеброй, где алгебраические структуры, такие как группы, кольца и поляаксиоматизируются и изучаются.
- Линейная алгебра, в которой изучаются свойства векторных пространств (включая матрицы).
- Универсальная алгебра, в которой изучаются свойства, общие для всех алгебраических структур.
- Алгебраическая теория чисел изучает свойства чисел в различных алгебраических системах. Теория чисел была создана путём расширения и обобщения алгебры.
- Алгебраическая геометрия применяет достижения алгебры для решения проблем геометрии.
- Алгебраическая комбинаторика, в которой методы абстрактной алгебры используются для изучения вопросов комбинаторики.
В некоторых напралениях углублённого изучения, аксиоматические алгебраические системы, такие как группы, кольца, поля и алгебры над полем на присутствие геометрических структур (метрик и топологий), совместимых с алгебраическими структурами. Список некоторых разделов функционального анализа:
- Нормированые линейные пространства
- Банаховы пространства
- Гильбертовы пространства
- Банаховы алгебры
- Нормированные алгебры
- Операторные алгебры
- Топологические группы
Элементарная алгебра
Элементарная алгебра — раздел алгебры, который изучает самые базовые понятия. Обычно изучается после изучения основных понятий арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (a,b,c,x,y и так далее). Такой подход полезен, потому что:
- Позволяет получить общее представление законов арифметики (например, a+b=b+a для любых a и b), что является первым шагом к систематическому изучению свойств действительных чисел.
- Позволяет ввести понятие «неизвестного», сформулировать уравнения и изучать способы их решения. (Для примера, “Найти число x, такое что 3x + 1 = 10” или, в более общем случае, “Найти число x, такое что ax + b = c”. Это приводит к выводу, что нахождение значения переменной кроется не в природе чисел из уравнения, а в операциях между ними.)
- Позволяет сформулировать понятие функции. (Для примера, “Если вы продали x билетов, то ваша прибыль составит 3x − 10 рублей, или f(x) = 3x − 10, где f — функция, и x — число, от которого зависит функция.”)
алгебра
| В Википедии есть страница «алгебра». |
Содержание
- 1 Русский
- 1.1 Морфологические и синтаксические свойства
- 1.2 Произношение
- 1.3 Семантические свойства
- 1.3.1 Значение
- 1.3.2 Синонимы
- 1.3.3 Антонимы
- 1.3.4 Гиперонимы
- 1.3.5 Гипонимы
- 1.4 Родственные слова
- 1.5 Этимология
- 1.6 Фразеологизмы и устойчивые сочетания
- 1.7 Перевод
- 1.8 Библиография
- 2 Башкирский
- 2.1 Морфологические и синтаксические свойства
- 2.2 Произношение
- 2.3 Семантические свойства
- 2.3.1 Значение
- 2.3.2 Синонимы
- 2.3.3 Антонимы
- 2.3.4 Гиперонимы
- 2.3.5 Гипонимы
- 2.4 Родственные слова
- 2.5 Этимология
- 2.6 Фразеологизмы и устойчивые сочетания
- 3 Белорусский
- 3.1 Морфологические и синтаксические свойства
- 3.2 Произношение
- 3.3 Семантические свойства
- 3.3.1 Значение
- 3.3.2 Синонимы
- 3.3.3 Антонимы
- 3.3.4 Гиперонимы
- 3.3.5 Гипонимы
- 3.4 Родственные слова
- 3.5 Этимология
- 3.6 Фразеологизмы и устойчивые сочетания
- 4 Болгарский
- 4.1 Морфологические и синтаксические свойства
- 4.2 Произношение
- 4.3 Семантические свойства
- 4.3.1 Значение
- 4.3.2 Синонимы
- 4.3.3 Антонимы
- 4.3.4 Гиперонимы
- 4.3.5 Гипонимы
- 4.4 Родственные слова
- 4.5 Этимология
- 4.6 Фразеологизмы и устойчивые сочетания
- 5 Казахский
- 5.1 Морфологические и синтаксические свойства
- 5.2 Произношение
- 5.3 Семантические свойства
- 5.3.1 Значение
- 5.3.2 Синонимы
- 5.3.3 Антонимы
- 5.3.4 Гиперонимы
- 5.3.5 Гипонимы
- 5.4 Родственные слова
- 5.5 Этимология
- 5.6 Фразеологизмы и устойчивые сочетания
- 6 Киргизский
- 6.1 Морфологические и синтаксические свойства
- 6.2 Произношение
- 6.3 Семантические свойства
- 6.3.1 Значение
- 6.3.2 Синонимы
- 6.3.3 Антонимы
- 6.3.4 Гиперонимы
- 6.3.5 Гипонимы
- 6.4 Родственные слова
- 6.5 Этимология
- 6.6 Фразеологизмы и устойчивые сочетания
- 7 Кумыкский
- 7.1 Морфологические и синтаксические свойства
- 7.2 Произношение
- 7.3 Семантические свойства
- 7.3.1 Значение
- 7.3.2 Синонимы
- 7.3.3 Антонимы
- 7.3.4 Гиперонимы
- 7.3.5 Гипонимы
- 7.4 Родственные слова
- 7.5 Этимология
- 7.6 Фразеологизмы и устойчивые сочетания
- 8 Лезгинский
- 8.1 Морфологические и синтаксические свойства
- 8.2 Произношение
- 8.3 Семантические свойства
- 8.3.1 Значение
- 8.3.2 Синонимы
- 8.3.3 Антонимы
- 8.3.4 Гиперонимы
- 8.3.5 Гипонимы
- 8.4 Родственные слова
- 8.5 Этимология
- 8.6 Фразеологизмы и устойчивые сочетания
- 9 Македонский
- 9.1 Морфологические и синтаксические свойства
- 9.2 Произношение
- 9.3 Семантические свойства
- 9.3.1 Значение
- 9.3.2 Синонимы
- 9.3.3 Антонимы
- 9.3.4 Гиперонимы
- 9.3.5 Гипонимы
- 9.4 Родственные слова
- 9.5 Этимология
- 9.6 Фразеологизмы и устойчивые сочетания
- 10 Марийский
- 10.1 Морфологические и синтаксические свойства
- 10.2 Произношение
- 10.3 Семантические свойства
- 10.3.1 Значение
- 10.3.2 Синонимы
- 10.3.3 Антонимы
- 10.3.4 Гиперонимы
- 10.3.5 Гипонимы
- 10.4 Родственные слова
- 10.5 Этимология
- 10.6 Фразеологизмы и устойчивые сочетания
- 11 Сербский
- 11.1 Морфологические и синтаксические свойства
- 11.2 Произношение
- 11.3 Семантические свойства
- 11.3.1 Значение
- 11.3.2 Синонимы
- 11.3.3 Антонимы
- 11.3.4 Гиперонимы
- 11.3.5 Гипонимы
- 11.4 Родственные слова
- 11.5 Этимология
- 11.6 Фразеологизмы и устойчивые сочетания
- 12 Таджикский
- 12.1 Морфологические и синтаксические свойства
- 12.2 Произношение
- 12.3 Семантические свойства
- 12.3.1 Значение
- 12.3.2 Синонимы
- 12.3.3 Антонимы
- 12.3.4 Гиперонимы
- 12.3.5 Гипонимы
- 12.4 Родственные слова
- 12.5 Этимология
- 12.6 Фразеологизмы и устойчивые сочетания
- 13 Татарский
- 13.1 Морфологические и синтаксические свойства
- 13.2 Произношение
- 13.3 Семантические свойства
- 13.3.1 Значение
- 13.3.2 Синонимы
- 13.3.3 Антонимы
- 13.3.4 Гиперонимы
- 13.3.5 Гипонимы
- 13.4 Родственные слова
- 13.5 Этимология
- 13.6 Фразеологизмы и устойчивые сочетания
- 14 Украинский
- 14.1 Морфологические и синтаксические свойства
- 14.2 Произношение
- 14.3 Семантические свойства
- 14.3.1 Значение
- 14.3.2 Синонимы
- 14.3.3 Антонимы
- 14.3.4 Гиперонимы
- 14.3.5 Гипонимы
- 14.4 Родственные слова
- 14.5 Этимология
- 14.6 Фразеологизмы и устойчивые сочетания
- 15 Чувашский
- 15.1 Морфологические и синтаксические свойства
- 15.2 Произношение
- 15.3 Семантические свойства
- 15.3.1 Значение
- 15.3.2 Синонимы
- 15.3.3 Антонимы
- 15.3.4 Гиперонимы
- 15.3.5 Гипонимы
- 15.4 Родственные слова
- 15.5 Этимология
- 15.6 Фразеологизмы и устойчивые сочетания
- 16 Якутский
- 16.1 Морфологические и синтаксические свойства
- 16.2 Произношение
- 16.3 Семантические свойства
- 16.3.1 Значение
- 16.3.2 Синонимы
- 16.3.3 Антонимы
- 16.3.4 Гиперонимы
- 16.3.5 Гипонимы
- 16.4 Родственные слова
- 16.5 Этимология
- 16.6 Фразеологизмы и устойчивые сочетания
Русский
| В Викиданных есть лексема алгебра (L85321). |
Морфологические и синтаксические свойства
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | а́лгебра | а́лгебры |
| Р. | а́лгебры | а́лгебр |
| Д. | а́лгебре | а́лгебрам |
| В. | а́лгебру | а́лгебры |
| Тв. | а́лгеброй а́лгеброю |
а́лгебрами |
| Пр. | а́лгебре | а́лгебрах |
а́л – геб – ра
Корень: -алгебр-; окончание: -а [Тихонов, 1996] .
Произношение
- МФА: ед. ч. [ ˈaɫɡʲɪbrə ], мн. ч. [ ˈaɫɡʲɪbrɨ ]
Семантические свойства
Значение
- раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающих обычные операции сложения и умножения чисел ◆ Отсутствует пример употребления (см. рекомендации ).
- то же, что элементарная алгебра, раздел алгебры [1], охватывающий свойства операций с вещественными и комплексными числами, а также правила тождественных преобразований математических выражений и уравнений с использованием символов, обозначающих такие числа, и элементарных функций ◆ Отсутствует пример употребления (см. рекомендации ).
- тип алгебраических структур; множество из каких-либо объектов, над элементами которого определены некоторые операции, являющиеся, как правило, обобщением сложения и умножения ◆ Отсутствует пример употребления (см. рекомендации ).
- книжн. сложная система навыков, знаний, методов в какой-либо области ◆ Нужны объективные методы оценки эффективности производств, включающие в себя не только арифметику, но и социальную алгебру нашей действительности. Марина Наумова, «Рыба ищет где глубже», 2001 г. ◆ Очень грубый подсчёт показывает абсолютное преобладание тех, кто может выиграть от дерегулирования занятости. Почему тогда реформы в этой сфере остаются столь сложными с политической точки зрения? Почему аргумент от простой арифметики в их поддержку недостаточен, а необходима хитроумная алгебра политических комбинаций? Владимир Гимпельсон, «Пора дерегулировать?», 2003 г.
Синонимы
- ?
- ?
- ?
- ?
Антонимы
- ?
- ?
- ?
- ?
Гиперонимы
- математика, наука
- ?
- ?
- ?
Гипонимы
- элементарная алгебра, высшая алгебра, линейная алгебра, общая алгебра, универсальная алгебра
- –
- группа, полугруппа, группоид, моноид, кольцо, полукольцо, поле, решётка
- ?
Родственные слова
Этимология
Происходит от арабск. الْجَبْر «восстановление, восполнение», от заглавия классической книги среднеазиатского математика Аль-Хорезми اَلْكِتَابُ ٱلْمُخْتَصَرُ فِي حِسَابٌ اَلْجَبْرُ وَٱلْمُقَابَلَةُ («Краткая книга о восполнении и уравновешивании», 825 г.), где под الْجَبْر понимается восполнение — операция переноса вычитаемых из одной части уравнения в другую, позволявшая избежать появления в уравнении, в современных терминах, унарного минуса, т.к. в то время исламская математика почти не умела обращаться с отрицательными числами. В свою очередь, الْمُقَابَلَة — уравновешивание или противопоставление — означала операцию вычитания из обеих частей уравнения подобных членов с положительными коэффициентами. Книга, где рассматривается решение различных линейных и квадратных уравнений, была переведена на латынь (1145 г., Роберт Честерский) под заглавием Liber Algebrae et Almucabola («Книга альджебры и альмукаболы») и стала известна европейским математикам под кратким названием Algebrа. Русск. алгебра — с 1717 года, заимств. через нем. Использованы данные словаря М. Фасмера. См. Список литературы.
ГДЗ Готовые домашние задания по Алгебре

Алгебра ЕМН Абылкасымова 11 класс 2020
Авторы: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.
Издательство: Мектеп

Алгебра Солтан 8 класс 2020
Авторы: Солтан Г., Солтан А., Жумадилова А.
Издательство: Келешек-2030

Алгебра Солтан 9 класс 2020
Авторы: Солтан Г., Солтан А., Жумадилова А.
Издательство: Келешек-2030

Алгебра Шыныбеков 9 класс 2019
Авторы: Шыныбеков А., Шыныбеков Д., Жумабаев Р.
Издательство: Атамұра

Алгебра и начало анализа ЕМН Шыныбеков 10 класс 2019
Авторы: Шыныбеков А., Шыныбеков Д., Жумабаев Р.
Издательство: Атамұра

Алгебра Абылкасымова 9 класс 2019
Авторы: Абылкасымова А., Кучер Т., Корчевский В., Жумагулова З.
Издательство: Мектеп

Алгебра Абылкасымова 10 класс 2019 Обще-гуманитарное направление
Авторы: Абылкасымова А., Жумагулова З.
Издательство: Мектеп

Алгебра Шыныбеков 8 класс 2018
Авторы: Шыныбеков А., Шыныбеков Д., Жумабаев Р.
Издательство: Атамұра

Алгебра Абылкасымова 8 класс 2018
Авторы: Абылкасымова А.Е., Кучер Т.П, Жұмағұлова З.Ә., Корчевский В.Е.
Издательство: Мектеп

Алгебра Абылкасымова 7 класс 2017
Авторы: Абылкасымова А.Е., Кучер Т.П., Корчевский В.Е., Жумагулова З.А.
Издательство: Мектеп

Алгебра Шыныбеков 7 класс 2017
Авторы: А.Н. Шыныбеков, Д.А. Шыныбеков
Издательство: Атамура
Алгебра Абылкасымова 8 класс 2016
Авторы: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А., Абдиев А.
Издательство: Мектеп
Алгебра Абылкасымова 10 класс Естественно-математическое направление
Авторы: Абылкасымова А.Е., Жұмағұлова З.А., Шойынбеков К.Д., Корчевский В.Е.
Издательство: Мектеп

Алгебра Абылкасымова 10 класс Общественно-гуманитарное направление
Авторы: Абылкасымова А.Е., Жұмағұлова З.А, Шойынбеков К.Д., Есенова М.И.
Издательство: Мектеп
Алгебра Шыныбеков 9 класс
Авторы: Шыныбеков А.Н.
Издательство: Атамура

Алгебра Абылкасымова 9 класс
Авторы: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.
Алгебра

Алгебра, изначально, — раздел математики, посвященный изучению операций над элементами множеств, которые могут так или иначе обобщать множества чисел, а операции — обобщать сложение и умножение. Требуя внимания на знаковых, а не пространственных объектах, алгебра противопоставляется геометрии и дополняет её. Синтез алгебры и геометрии доставляет алгебраическая геометрия. Исторически алгебра зародилась при решении уравнений, и её истоки берут начало в работах арабских математиков.
Ныне «алгеброй» того или иного рода могут называться всевозможные математические объекты, изучение которых началось с изучения самого языка, которыми описывались свойства чисел в изначальной традиции алгебры. Ранним примером такого объекта служит булева алгебра.
Содержание
[править] История алгебры
Арифметика изучается с самых древних сохранившихся текстов, относимых к математике. В нынешних справочниках признается, что на развитие алгебры оказал влияние труд древнегреческого математика Диофанта Александрийского «Арифметика» (3 век с рождества Христова).
В труде арабского математика Мухаммеда аль-Хорезми под названием «Альджебр аль-мукабала» (9 век нашей эры), рассмотрены методы решения задач, сводящихся в современной терминологии к алгебраическим уравнениям первой и второй степеней. От названия этой работы и произошел термин «алгебра».
В 15-17 веках в работах европейских математиков появились применяемые в настоящее время обозначения алгебраических операций («+», «-»), скобки, знаки радикалов, обозначение степеней числа. Франсуа Виет в конце 16 века ввел буквенные обозначения для переменных.
В 17-18 веках под алгеброй понимается наука о вычислениях с использованием переменных, записанных с помощью букв, в частности решение алгебраических уравнений. В настоящее время в школьном образовании подобные буквенные вычисления называются элементарной алгеброй.
Задача о нахождении корней общего алгебраического уравнения n-й степени
с помощью элементарных арифметических операций и операции извлечения корней становится центральной задачей алгебры.
Итальянскими математиками в 15 веке были найдены формулы для решения общего уравнения 3-й и 4-й степени, однако для более высоких степеней задача до 19 века не поддавалась решению.
В 1824 году норвежский математик Нильс Абель доказал, что уравнения выше 4-й степени в общем случае в радикалах не разрешимы. В 1830 году французский математик Эварист Галуа в рамках созданной им теории Галуа вывел общий критерий разрешимости алгебраического уравнения в радикалах.
С середины 19 века в центре алгебраических исследований оказывается изучение произвольных алгебраических операций. Так расширялось понятия числа, появилось понятие алгебра логики, были исследованы кватернионы, создано матричное исчисление, получила развитие теория групп.
Алгебра как общая теория произвольных алгебраических операций стала восприниматься с начала 20 века с появлением работ Давида Гильберта, Э. Штейница, Э. Артина, Эмми Нётер. Это понимание было закреплено в вышедшей в 1930 году монографии Б. Л. ван дер Вардена «Современная алгебра», остающейся до настоящего времени востребованным учебником по алгебре.
[править] Предмет алгебры
Предметом изучения современной алгебры являются множества с заданными на них алгебраическими операциями. При этом если между такими множествами можно установить изоморфизм (взаимно-однозначное соответствие, сохраняющее операции), то множества считаются одинаковыми, и поэтому природа множеств безразлична. Следовательно, объектом изучения алгебры являются сами алгебраические операции.
Примером изучаемого в рамках алгебры множества с операцией является группа: множество с одной ассоциативной бинарной операцией, содержащее единицу и для каждого элемента — обратный элемент. Понятие группы появилось в теории Галуа в 19 веке, в которой группы сопоставлялись уравнениям, а условием разрешимости уравнения в радикалах оказалась разрешимость соответствующей группы. В дальнейшем были изучены такие обобщения групп, как полугруппы, квазигруппы и лупы.
В рамках алгебры изучаются такие алгебраические множества с двумя бинарными операциями как кольца и поля. В этих структурах одна из операций называется сложением (она коммутативна и каждый элемент имеет обратный), а другая операция — умножением (обычно, она предполагается ассоциативной, хотя могут изучаться и неассоциативные кольца).
В рамках линейной алгебры изучается линейное пространство с операцией сложения, а также с умножением на элементы основного поля (скаляры). Модуль — обобщение линейного пространства, в нем вместо поля скаляров элементы модуля умножаются на элементы кольца, которое берется вместо основного поля.
Внесение дополнительных структур, согласованных с алгебраическими операциями, привело к появлению новых разделов алгебры, пограничных с другими разделами математики. Это топологическая алгебра, включая теорию топологических групп и групп Ли, теория нормированных колец, дифференциальная алгебра. Как самостоятельную дисциплину можно рассматривать гомологическую алгебру.
[править] Роль алгебры в математике
Математик Игорь Шафаревич в своей книге «Алгебра — 1» вслед за математиком и философом Германом Вейлем видит роль алгебры в математике в том, что она занимается координатизацией математических объектов.
Вместе с фундаментальной ролью внутри математики алгебра применяется в прикладных областях. Теория представлений групп используется в физике, дискретные группы применяются в кристаллографии. Алгебраические методы используются в криптографии, теории кодирования, математической экономике. Абстрактная алгебра охватывает возможности вычислений.
ГДЗ по алгебре 7 класс

Авторы: Журавлев, Перепелкина
Издательство: Экзамен
Тип книги: Рабочая тетрадь

Авторы: Ерина
Издательство: Экзамен
Тип книги: Рабочая тетрадь

Авторы: Мерзляк, Полонский, Якир
Издательство: Вентана-Граф
Тип книги: Учебник

Авторы: Дорофеев, Суворова, Бунимович, Минаева, Рослова
Издательство: Просвещение
Тип книги: Учебник

Авторы: Ключникова, Комиссарова
Издательство: Экзамен
Тип книги: Рабочая тетрадь

Авторы: Гусева, Пушкин, Рыбакова
Издательство: Интеллект-Центр
Тип книги: Тестовые материалы для оценки качества обучения

Авторы: Чулков
Издательство: Просвещение
Тип книги: Тематические тесты

Авторы: Минаева, Рослова
Издательство: Просвещение
Тип книги: Рабочая тетрадь

Авторы: Лебединцева, Беленкова
Издательство: Интеллект-Центр
Тип книги: Задания для обучения и развития учащихся

Авторы: Зубарева, Мильштейн
Издательство: Мнемозина
Тип книги: Рабочая тетрадь

Авторы: Колягин, Ткачева
Издательство: Просвещение
Тип книги: Рабочая тетрадь

Авторы: Миндюк, Шлыкова
Издательство: Просвещение
Тип книги: Рабочая тетрадь

Авторы: Муравин, Муравина
Издательство: Дрофа
Тип книги: Рабочая тетрадь
В седьмом классе вместо одного предмета – математики – становится целых два: алгебра и геометрия. На этом этапе сложных формул и терминов появляется еще больше, чем в предыдущие годы учебы. В программе алгебры рассматривается множество тем:
- тождества с натуральными и дробными числами;
- системы линейных уравнений с двумя переменными;
- одночлены и многочлены;
- степени с натуральным показателем и пр.
Понять и запомнить все это бывает сложно. Требования учителей возрастают, получать хорошие оценки становится тяжелее, а свободного времени катастрофически не хватает. В такие моменты на помощью приходят решебники с готовыми домашними заданиями.
На нашем портале собраны ГДЗ для учебников 7 класса от разных авторов:
- Журавлев;
- Перепелкина;
- Ключникова;
- Комиссарова и др.
Пособия подходят ко всем основным учебникам, которые используют в большинстве российских школ. С решебниками можно качественно готовить домашние задания и выполнять все упражнения.
Как помогают онлайн-решебники в 7 классе
Решебники нашего портала содержат ответы ко всем задачам в учебнике вне зависимости от сложности. Можно посмотреть решение, научиться делать по аналогии и получать отличные оценки.
Благодаря ГДЗ больше не обязательно обращаться к репетиторам. Любой сложный материал можно разобрать самостоятельно. А пользоваться решебниками легко: достаточно найти подходящее пособие и номер задания в нем. Все решения составлены и перепроверены специалистами с большим опытом и стажем, так что в их правильности не приходится сомневаться.
Выполненные с помощью наших решебников домашние задания:
- будут оценены на отличную оценку даже самым требовательным учителем;
- помогут разобраться в сложном материале;
- подойдут для повторения пройденных тем;
- могут использоваться для самопроверки.
Даже если школьник пропустил какой-то материал, он не отстанет в таком сложном предмете, как алгебра, и быстро будет развивать свои способности. Ведь этот раздел математики многим действительно дается нелегко и требует хорошего аналитического мышления. Просто знания теории не помогают, нужно понимать принцип решения и отлично в нем разбираться.
ГДЗ подойдут не только школьникам, но и родителям, которые хотят помогать своему ребенку в учебе и контролировать его знания. Кроме того, это хорошее подспорье учителям, которые смогут быстрее проверять домашнее задание, а также составлять карточки для самостоятельных работ.
ГДЗ по алгебре 7 класс

Авторы: А. Г. Мерзляк, В. Б. Полонский, М. С. Якир
Издательство: Вентана-Граф
Тип книги: Учебник

Авторы: Г. В. Дорофеев, Е. А. Бунимович, Л. В. Кузнецова, С. С. Минаева, С. Б. Суворова, Л. О. Рослова.
Издательство: Просвещение
Тип книги: Учебник

Авторы: Г. К. Муравин, О. В. Муравина
Издательство: Дрофа
Тип книги: Рабочая тетрадь

Авторы: Е. М. Ключникова, И. В. Комиссарова
Издательство: Экзамен
Тип книги: Рабочая тетрадь

Авторы: Т. М. Ерина
Издательство: Экзамен
Тип книги: Рабочая тетрадь

Авторы: Н. Г. Миндюк, И. С. Шлыкова
Издательство: Просвещение
Тип книги: Рабочая тетрадь

Авторы: С. Г. Журавлев, Ю. В. Перепелкина
Издательство: Экзамен
Тип книги: Рабочая тетрадь

Авторы: Ю. М. Колягин, М. И. Шабунин, Н. Е. Федорова, М. В. Ткачева
Издательство: Просвещение
Тип книги: Рабочая тетрадь

Авторы: С. С. Минаева, Л. О. Рослова
Издательство: Просвещение
Тип книги: Рабочая тетрадь

Авторы: Е. А. Лебединцева, Е. Ю. Беленкова
Издательство: Интеллект-Центр
Тип книги: Задания для обучения и развития учащихся

Авторы: И. И. Зубарева, М. С. Мильштейн
Издательство: Мнемозина
Тип книги: Рабочая тетрадь
В седьмом классе математика как дисциплина делится на алгебру и геометрию. Темы становятся сложнее, не всегда получается справиться с домашней работой быстро и без ошибок. ГДЗ экономят время, выручают в тех случаях, когда вопросов больше, чем вариантов решения.
Мы собрали решебники по алгебре для седьмого класса не только к учебникам, но и к рабочим тетрадям. Они доступны онлайн бесплатно и в хорошем качестве.
Для чего нужны ГДЗ:
- проверить свои знания;
- найти ответ тогда, когда совсем нет идей, как решить задание;
- подготовиться к контрольной работе;
- для экономии времени.
Многим школьникам и их родителям уже в седьмом классе сложно самостоятельно разбираться в заданиях и упражнениях. Для этого разработаны решебники с готовыми ответами. Нам важно, чтобы каждый школьник смог понять тему урока и выполнить домашнее задание без ошибок. Не забывайте, что списать готовое решение — простой путь, который не ведет к знаниям. Используйте ГДЗ для самопроверки и тренировки знаний.