Функция y=k/х – свойства, график и примеры решения задач

Функция « y = kx » и её график

Прежде чем перейти к изучению функции « y = kx » внимательно изучите урок
«Что такое функция в математике» и «Как решать задачи на функцию».

Функция « y = kx » — это первый тип функции, который изучается в математике.

Буквенный множитель « k » в функции « y = kx » называют числовым коэффициентом .

На месте « k » может стоять любое число (положительное, отрицательное или дробь).

Другими словами, можно сказать, что « y = kx » — это семейство всевозможных функций, где вместо « k » стоит число.

Примеры функций вида « y = kx ».

y = 4x
y = −1,5x
y =
1
2
x

Давайте определим для каждой из функций выше, чему в них равен числовый коэффициент « k » .

Как построить график функции « y = kx »

Графиком функции « y = kx » является прямая .

Из геометрии вспомним аксиому (утверждение, которое не требует доказательства), что через любые две точки можно провести прямую и притом только одну.

Исходя из этой аксиомы, что чтобы построить график функции вида « у = kx » нам будет достаточно найти всего две точки.

Для примера построим график функции « y = −4x ».

Найдем значение функции « y » для двух произвольных значений « x ». Подставим, например, вместо « x » числа « 0 » и « 1 ».

Выбирая произвольные числовые значения вместо « x », лучше брать числа « 0 » и « 1 ». С этими числами легко выполнять расчеты.

x	Расчет « y »
0	y(0) = −4 · 0 = 0
1	y(1) = −4 · 1 = −4

Полученные значения « x » и « y » — это координаты точек графика
функции « y = −4x ».

Запишем полученные координаты точек « y = −4x » в таблицу.

Точка	Координата по оси « Оx » (абсцисса)	Координата по оси « Оy » (ордината)
(·)A	0	0
(·)B	1	−4

Отметим полученные точки на системе координат.

Теперь проведем прямую через отмеченные точки. Эта прямая и будет являться графиком функции « y = −4x ».

После построения не забудьте подписать график функции.

Как решать задачи на функцию « y = kx »

Построить график функции « y = −1,5x ». Найти по графику:

значение « y » соответствующее значению « x » равному 1; 0; 2; 3 ;
значение « x », если значение « y » равно −3; 4,5; 6 ;
несколько целых значений « x », при которых значения « y » положительны (отрицательны).

Вначале построим график функции « y = −1,5x ».

Используем правила, по которым мы строили график функции выше. Для построения графика функции « y = −1,5x » достаточно найти всего две точки.

Выберем два произвольных числовых значения для « x ». Для удобства расчетов выберем числа « 0 » и « 1 ».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси « Оx »	Координата по оси « Оy »
(·)A	0	y(0) = −1,5 · 0 = 0
(·)B	1	y(1) = −1,5 · 1 = −1,5

Отметим полученные точки на прямоугольной системе координат.

Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции « y = −1,5x ».

Теперь работаем с построенным графиком функции « y = −1,5x ».

Требуется найти значение « y », соответствующее значению « x » равному 1; 0; 2; 3 .

Тему «Как получить координаты точки функции» с графика функции мы уже подробно рассматривали в уроке «Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

Чтобы найти значение « y » по известному значению « x » на графике функции необходимо:

провести перпендикуляр от оси « Ox » (ось абсцисс) из заданного числового значения « x » до пересечения с графиком функции;
из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси « Oy » (ось ординат);
полученное числовое значение на оси « Oy » и будет искомым значением.

По правилам выше найдем на построенном ранее графике функции « y = −1,5x » необходимые значения функции « y » для « x » равным 1; 0; 2; 3 .

Запишем полученные результаты в таблицу.

Заданное значение « x »	Полученное с графика значение « y »
0	0
1	−1,5
2	−3
3	−4,5

Переходим ко второму заданию задачи. Требуется найти значение « x », если значение « y » равно −3; 4,5; 6 .

Выполним те же действия, что и при решении предыдущего задания. Разница будет лишь в том, что изначально мы будем проводить перпендикуляры
от оси « Oy ».

Запишем полученные результаты в таблицу.

Заданное значение « y »	Полученное с графика значение « x »
−3	2
4,5	−3
6	−4

Перейдем к последнему заданию. Нас просят найти несколько целых значений « x », при которых значения « y » положительны (отрицательны).

Для решения этой задачи необходимо внимательно изучить
график функции « y = −1,5x ».

Отметим область на оси « Oy », где значения « y » для графика функции « y = −1,5x » положительны.

Из этой области проведем от графика функции несколько перпендикуляров к оси « Ox » .

Помните, что по заданию, нас просят найти несколько «целых» значений « x ». Поэтому перпендикуляры мы будем проводить к оси « Ox » в целые числовые значения.

Запишем ответ. При x = −2; x = −1 значения y > 0 .

Теперь найдем при каких « x », значения « y » отрицательны. Отметим область на оси « Oy », где значения « y » на графике функции отрицательны.

Проведем перпендикуляры из отмеченной области к оси « Ox » в целые числовые значения « x ».

Запишем ответ. При x = 1; x = 2 значения y .

Рассмотрим другую задачу.

Какие из точек A(5; −3) , D(2; 1) принадлежат графику функции, заданной
формулой « y =

x »?

Подробный разбор задачи «Как проверить, что точка принадлежит графику функции» мы приводили в уроке «Как решать задачи на функцию».

В этом уроке мы вспомним только основные моменты решения подобных задач.

Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.

Достаточно подставить координаты точки в формулу функции (координату по оси « Ox » вместо « x », а координату по оси « Oy » вместо « y ») и выполнить арифметические расчеты.

Если получится верное равенство, значит точка принадлежит графику функции.
Если получится не верное равенство, значит точка не принадлежит графику функции.

Функция y=k/х свойства и график, область определения функции, коэффициент в графике функции, примеры решения задач

Во время решения задач по математике учащиеся сталкиваются с функцией у = к/х, которую нужно не только обследовать, но и построить ее график. Очень часто новички делают много ошибок, поскольку считают, что только прямая имеет такое уравнение. Для получения знаний в исследовании следует ознакомиться подробно со свойствами и формулами.

Общие сведения

Функцией называется некоторая зависимость переменных друг от друга. В некоторых случаях неизвестные величины могут быть выражены системой конкретных значений, интервалами, а также другими функциональными выражениями. Последний класс называется сложным или составным. Различают зависимые и независимые переменные (аргументы). Второй тип может принимать любые значения, кроме тех, которые превращают выражение в неопределенность.

Однако аргументы необходимо также обследовать, поскольку они могут обратить тождество в пустое множество. Одним из таких примеров является функция у = к / х. Ее аргумент x может принимать любые значения, кроме 0. Именно это число превращает уравнение в неопределенность, поскольку в математике существует следующее правило: запрещается делить на 0.

Следует отметить, что существует функция y = k/x и ее график — кривая, имеющая название гипербола. Многие путают его с параболой (в степени 2). Однако она является квадратичной. График строится в системе координат, которая называется декартовой. Кроме того, в математике встречается еще одно уравнение вида y = кх. Ее графиком является прямая.

Прямоугольная система координат

В математике существуют специальные инструменты для построения графиков функций. Одним из них считается распространенная прямоугольная система координат. Она может быть на плоскости и в пространстве. Поскольку y = k/x и y = kx являются элементарными, то для иллюстрации их графиков используется однородная прямоугольная декартовая система координат (рис. 1), элементом которой является точка.

Для декартовой системы на плоскости имеется только две координаты: по взаимно перпендикулярным осям ординат (ОУ) и абсцисс (ОХ). Они пересекаются в некоторой точке О, которая называется началом координат.

Рисунок 1. Прямоугольная декартова система координат (ДСК).

При указании координат нужно учитывать четверть. От нее зависит знак. Оси ординат (игрек) и абсцисс (икс) делят систему на четыре четверти. Они обозначаются римскими цифрами (рис. 1) и имеют такие свойства:

Первая — I: координаты x и y являются положительными числами, т. е. x > 0 и y > 0.
II: x 0.
III: x 0 и y Коэффициент пропорциональности

В математических дисциплинах бывает два типа пропорциональности — прямая и обратная. Они применяются для описания различных процессов, исследования дифференциальных уравнений, физических величин и законов.

Прямой пропорциональностью называется некоторая линейная функция вида y = kx, в которой аргументом является х, а к — коэффициент прямой пропорциональности. Иными словами, произведение к на аргумент x есть величина, определяющая прямую пропорциональную зависимость одной величины от другой. Обратной пропорциональностью называется некоторая функция вида y = k/x, значение аргумента которой никогда не равно нулю.

Графиком линейной функции вида y = kx является прямая, проходящая через начало координат в точке О(0;0). От к зависит угол наклона прямой. Если к > 0, то он является острым, т. е. его значение меньше 90 градусов. При к 0, то она располагается в I и III. Когда к Исследование функции

Для полного анализа поведения функции применяется методика или алгоритм ее исследования. Это нужно прежде всего для подробного графика. Однако перед началом выполнения этой операции следует ознакомиться с основными пунктами полного исследования заданной функции. К ним относятся следующие:

Область определения — D(f).
Область допустимых значений — E(f).
Нули.
Знаковые промежутки.
Периодичность.
Параметры четности.
Экстремумы (MAX и MIN).
Монотонность (интервалы).

Однако некоторые пункты можно опускать или менять местами. После этого необходимо строить график, учитывая все необходимые материалы исследования. Следует подробно разобрать каждый пункт, поскольку только верное решение дает возможность построить правильный график. Кроме того, специалисты рекомендуют освоить интервалы и их правильную запись.

Правила записи интервалов

В некоторых пунктах алгоритма исследования функции встречается термин «промежуток» или «интервал». От правильности его задания зависит решение задачи. Во всем мире приняты обозначения, которые помогут сделать запись понятной и грамотной:

Обозначение жесткой границы (включительно) квадратными скобками [], а значения, не входящего в интервал (не включительно), — круглыми скобками ().
Тип границ можно комбинировать.
Для объединения промежутков применяется специальный символ U.
Бесконечность можно обозначать символом или inf. Например, (-inf;inf).
Перед и после бесконечности всегда ставится круглая скобка.
Порядок комбинации промежутков (интервалов или числовых отрезков): последовательно от большего к меньшему. Например, (-inf;-8) U (-4;0] U [5;8] U (10;15).

Обозначение inf используется в некоторых языках программирования или математических пакетах. В дисциплине «Алгебра и начало анализа» интервалы встречаются очень часто, поскольку она основана на исследовании выражений, уравнений, неравенств, функций и т. д. После ознакомления с правилами записи промежутков следует переходить к первому пункту — нахождению D(f).

Область определения и допустимые значения

Все значения аргумента, при которых существует заданная функция вида z = f(y), называется областью ее определения. Обозначается параметр комбинацией букв D(имя функции), т. е. D(z) или D(f(y)). Величина D(z) зависит от типа функции, в том числе от ее сложности. Если она состоит из нескольких простых элементов, то нужно рассматривать D(z) для каждого из них. Параметр всегда записывается в виде промежутка, на котором существует зависимая переменная.

Областью допустимых значений функции z = f(y) являются все значения, при которых она существует. Обозначается величина литерой Е(имя функции). Например, запись для z = f(y) выглядит таким образом: Е(z) или Е(f(y)). Этот параметр тоже зависит от типа выражения, как и D(z). Задается в виде интервала. Для его задания необходимо выяснить, при каких значениях функция не существует. Например, для z = 2 / y. В искомом выражении у не может быть равен 0. Следовательно, у принадлежит следующему интервалу: (-inf;0) U (0;inf). Для z = 3y параметр Е(z) = (-inf;inf), поскольку при любых значениях функция существует.

Нули и знаковые промежутки

Нулями функции называются все значения независимой переменной, при которых ее график пересекается с осями ОУ и ОХ. Для нахождения точки пересечения с ОУ необходимо подставить х = 0 в выражение и выполнить расчеты. Чтобы найти пересечение или пересечения с осью иксов, нужно решить уравнение, приравняв его к 0.

Знаковые промежутки (интервал знакопостоянства) — отрезки, на которых функция меняет знак на противоположный. Если интервал положительный, то короткая запись выглядит таким образом: f(x) > 0 при х, принадлежащим промежутку (2;6) U [8;10]. Аналогично указывается отрезок, на котором заданная функция принимает отрицательные значения (f(x) Периодичность и четность

Периодической является функция, повторяющая значения через некоторый период Т (регулярный интервал). Ее значения не меняются при добавлении к аргументу некоторого числа, неравного нулевому значению. Математическая запись для z = f(y) имеет такой вид: z = f(y + T) = f(y — T). Для любой периодической функции справедливо также следующее равенство: z = f(y + nT). Коэффициент n — любое целочисленной значение.

Для выявления признака четности следует воспользоваться очень простым соотношением f(y) = f(-y). Для этого необходимо подставить в выражение положительное, а затем отрицательное значение аргумента. Если в первом и втором случаях равенство будет выполняться, то можно сделать вывод о четности. Когда соотношение не выполняется, тогда исходная функция является нечетной.

Монотонность и экстремумы

Монотонная — функция z = f(x), которая может только возрастать или убывать (понижение) на всей области определения. Для исследования нужно воспользоваться следующим алгоритмом:

Найти первую производную.
Определить критические точки, приравняв производную к 0.
Выяснить знаки производной на промежутках.
Сделать выводы.

Далее нужно определить экстремумы, т. е. минимальное и максимальное значения функции на всей области ее определения. В этом случае также существуют определенные правила:

Найти D(z) и сравнить его с отрезком, на котором нужно найти экстремумы (должен принадлежать D(z)).
Найти производную заданной функции.
Выполнить поиск стационарных точек (производная приравнивается к 0 и решается уравнение).
Подставить корни уравнения в исходную функцию.
Найти минимальное и максимальное значения.

Следует учесть все точки. Однако перед выполнением 4 пункта следует отсеять ложные корни. Для этого следует подставить в уравнение корни. Они должны соответствовать равенству. Если этого не происходит, то корень отсеивается.

Информация о свойствах

В некоторых источниках описываются свойства y = k/x и ее график. Следует отметить, что они получаются при исследовании последней. Существует два состояния. При первом коэффициент пропорциональности больше 0 (k > 0). Следовательно, она обладает такими свойствами:

График: кривая-гипербола.
D(y) = (-inf;0) U (0;+inf).
Если x > 0, то y > 0.
При отрицательных величинах аргумента функция принимает отрицательные значения.
Она убывает на интервалах: (-inf;0) и (0;+inf).
Точек экстремума нет.
Непрерывна, кроме точки х = 0.
Непериодическая.
Нечетная.

Когда к 0 при отрицательных значениях аргумента, а y 0. Функция y = kx обладает такими свойствами (k > 0):

График: прямая.
D(y) = (-inf;+inf).
Если x > 0, то y > 0. Когда x 0 при x Пример решения

Существует некоторый тип задач, в которых нужно исследовать и построить график функции y = k/x. Разобрать решение можно на примере y = 5 / (x — 3). Следует воспользоваться алгоритмом:

D(5 / (x — 3)) = (-inf;3) U (3;+inf).
Нули функции. По ОУ: y = 5 / (0 — 3) = — 5/3. По ОХ: 5 / (x — 3) = 0. Если решить уравнения, то у него нет корней.
Знаковые промежутки: (-inf;3) и (3;+inf).
Непериодическая.
Четность: 5 / (-x — 3) = — 5 / (x + 3). Нечетная: — 5 / (x + 3) не равно 5 / (x — 3).
Экстремумы: y’ = [5 / (x — 3)] = — 5 / (x — 3)^2 = 0. Уравнение не имеет решений, а это значит, что максимума и минимума нет.
Не является монотонной.

Чтобы построить график функции y = k / x + 3 (к = 5), нужно составить таблицу для его построения.

х	-4	-3	-2	-1	0	1	2	3	4
у	-5/7	-5/6	-1	-1,2	-5/3	-2,5	-5	нет	5

Таблица 1. Зависимость значения функции от ее аргумента.

После составления таблицы нужно начертить ДСК. На ней следует отмечать точки, а затем их плавно соединить (рис. 2).

Рисунок 2. График обратной пропорциональности y = k / x — 3 при к = 5.

Математики рекомендуют для проверки применять специализированные веб-приложения. Одним из них является онлайн-сервис, который называется yotx.

Таким образом, графиком обратной пропорциональности является гипербола, а прямой пропорциональности — прямая. Поведение функции исследуется по специальному алгоритму, который позволяет легко построить ее график и выяснить некоторые свойства.

Функция y=k/x и ее график

Урок 8. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Функция y=k/x и ее график”

Давайте рассмотрим пример:

Пусть расстояние в 200 км автомобиль со скоростью равной v км/ч преодолеет за время равное t часов. Тогда используя формулу пути, зависимость времени от скорости движения автомобиля при равном расстоянии можно выразить формулой:

Напомню, что такую зависимость называют обратно пропорциональной. Т.к. при увеличении одной величины вторая величина будет уменьшаться.

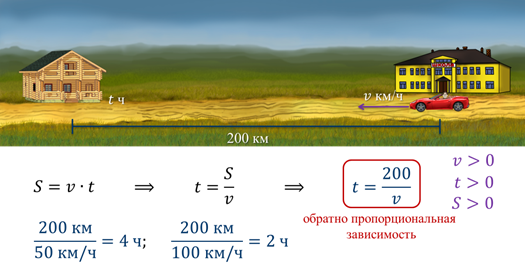
Вот, например, если автомобиль будет ехать со скоростью 50 км/ч, то на преодоление расстояния в 200 км ему понадобится 4 часа.

А вот, если автомобиль будет ехать со скоростью 100 км/ч, то на преодоление этого же пути, ему понадобится всего лишь 2 часа. Видим, что при увеличении скорости, времени тратится меньше.

Но в этой задаче переменные v и t могут принимать лишь положительные значения, т.к. скорость, время и расстояние это положительные величины.

В дальнейшем мы будем рассматривать функции, задаваемые формулой вида:

Такие функции называют обратными пропорциональностями.

С обратной пропорциональностью мы с вами часто встречаемся в повседневной жизни.

Масса m кг конфет, которую можно купить на 1 000 рублей по цене p рублей за кг. Зависимость массы конфет от стоимости за килограмм является обратно пропорциональной. Или, если есть прямоугольник длина которого a см, а ширина b см с площадью равной 27 см 2 . Такая зависимость также является обратно пропорциональной.

Определение:

Обратной пропорциональностью называется функция, которую можно задать формулой вида:

где x – независимая переменная и k – не равное 0 число.

Число k – называют коэффициентом обратной пропорциональности.

В нашем примере

Областью определения функции, заданной формулой вида:

является множество действительных чисел, отличных от нуля, т.к. выражение имеет смысл при любых x, кроме x равное нулю.

Теперь давайте построим график обратной пропорциональности .

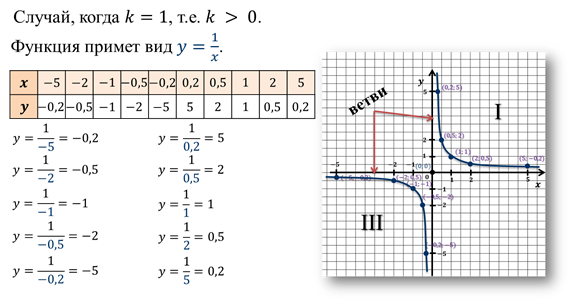
Полученный график состоит из двух симметричных относительно начала координат частей. Их обычно называют ветвями. Одна из этих ветвей расположена в первой четверти, вторая – в третьей.

График функции при любом k > 0 имеет такой же вид, что и график функции .

Теперь построим график функции .

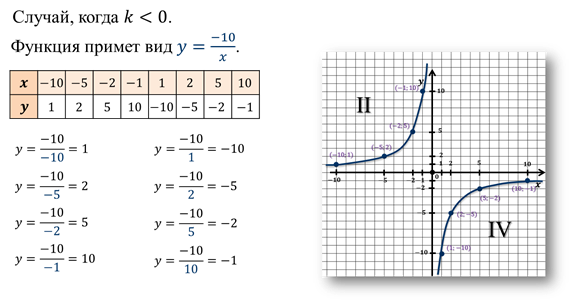
Такой же вид имеет график функции при любом k 0 ветви гиперболы лежат в 1-ой и 3-ей четвертях. При k Оцените видеоурок

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х – 2. Значит:

если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0;
и т. д.

Для удобства результаты можно оформлять в виде таблицы:

х	0	2	4
y	-2	-1	0

Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».

Свойства линейной функции

Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит y = b — четная;
b = 0, k ≠ 0, значит y = kx — нечетная;
b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (-b/k, 0);
ось ординат OY — в точке (0; b).
x=-b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, – b /_k) и положительные значения на промежутке (- b /_k, +∞)
При k b /_k, +∞) и положительные значения на промежутке (-∞, – b /_k).
Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1 /₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 1 /₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = – 1 /₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x – 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
график функции y = 2x – 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k 0, то график функции y = kx + b выглядит так:

0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = – b /_k.
Координаты точки пересечения с осью OX: (- b /_k; 0)

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
2 = -4(-3) + b
b = -10
Таким образом, нам надо построить график функции y = -4x – 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.

Функция y=k/x и ее график
план-конспект урока по алгебре (8 класс) на тему

Образовательная цель:

– научить строить график функции y= k/x опираясь на свойства функции;

– ввести понятие функции обратной пропорциональности;

– сформировать чёткое представление о различиях свойств и расположения графика функции при различных значениях k;

– расширить представления учащихся о функциях.

Развивающая цель:

– продолжить развитие познавательного интереса к изучению понятия функции;

– развивать умение анализировать, наблюдать, сопоставлять, логически мыслить;

– продолжить развитие элементов творческой деятельности учащихся, через вовлечение их в работу частично поискового характера, развитие навыков взаимоконтроля и самоконтроля.

Воспитывающая цель:

– воспитание навыков коммуникативности в работе, умение слушать и слышать другого, уважение к мнению товарища;

– воспитание у учащихся таких нравственных качеств, как настойчивость, аккуратность, инициативность, точность, привычка к систематичному труду, самостоятельность, активность;

– воспитание культуры общения.

Скачать:

Вложение	Размер
функция y=k/x	219.5 КБ

Предварительный просмотр:

Урок-открытие новых знаний

(Алгебра. 8 класс: учебник. Ю. Н. Макарычев)

Тема урока “Функция k/x и ее график “

Тип урока : изучение нового материала

– научить строить график функции y= k/x опираясь на свойства функции;

– ввести понятие функции обратной пропорциональности;

– расширить представления учащихся о функциях .

– продолжить развитие познавательного интереса к изучению понятия функции;

– развивать умение анализировать, наблюдать, сопоставлять, логически мыслить;

– воспитание культуры общения.

– проектор, компьютер, экран, раздаточный материал.

– Презентация к уроку.

1. Организационный момент

2. Повторение изученного

Учитель : Сегодня на уроке мы продолжаем знакомиться с новыми функциями, их свойствами и графиком.

Чтобы определить учебные задачи нашего урока выполним следующую работу.

( У каждого ученика на парте раздаточный материал с заданием, необходимо ответить на вопрос, найти верный ответ среди предложенных,

соответствующую букву записать в таблицу под правильным ответом ).

Учитель: Какое слово получили? ( Гипербола )

Что это за слово в математике?

3. Изучение нового материала

Ученик выступает с сообщением: (это график некоторой функции. Одним из первых, кто начал изучать эту кривую был ученик знаменитого Платона, древнегреческий математик Менехм в IV в. до н.э., но так и не сумел её полностью изучить. А вот полностью исследовал свойства гиперболы и дал ей название крупнейший геометр древности Аполоний Пергский в III в. до н.э.).

Учитель: Сегодня мы с вами побываем в роли древнегреческих ученых.

Как вы думаете, какие задачи мы должны поставить и решить на уроке?

(Учащиеся пытаются сформулировать эти задачи с помощью учителя).

Выяснить графиком какой функции является гипербола.

Рассмотреть расположение графика функции в системе координат.

Изучить свойства функции

Помогут ответить на вопросы следующие задания:

а) С увеличением цены за единицу товара количество товара, которое можно закупить на данную сумму денег … уменьшится

б) С уменьшением скорости движения на данном отрезке пути время движения … увеличится

в) С увеличением производительности труда при выполнении данного объёма работы количество рабочих … уменьшится

(Учитель читает задачу, учащиеся отвечают на вопрос, учащиеся записывают в тетради, один ученик на доске)

Пешеход проходит путь S со скоростью v за t часов. Выразите время пешехода через путь и скорость.

Найдите значение t при S=60 и V=0,5; 1; 2; 4; 16; 60; 120.

Какая зависимость между временем нахождения в пути и скоростью?

Как можем записать формулу в общем виде?

Функция, заданная формулой где k 0, называется обратной пропорциональностью.

Учитель : Детально рассмотрим эту зависимость с помощью графика на примере функции .

Как построить график незнакомой нам функции?

А как вы думаете, как будет называться график этой функции?

Построение графика функции.

Составить таблицу значений (взять значения аргумента с расчетом, чтобы положение графика определялось с достаточной полнотой).

Отметить точки на координатной плоскости.

Соединить точки линией.

(Все учащиеся строят в тетради, один ученик на доске)

Учитель: Давайте перечислим свойства этой функции.

(Учащиеся с помощью учителя перечисляют свойства построенной функции).

Учитель: А как вы думаете, если мы возьмем отрицательное число k,

Что произойдет с расположением графика в системе координат?

Исследовательская работа в парах.

Задание . Построить график функции и описать свойства?

(Учащиеся выполняют задания в парах, после выполнения один из учеников записывает свойства на доске).

Учитель : Что произошло с графиком функции, при изменении коэффициента?

4. Первичное закрепление

Выполнение номеров: 182, 185, 181, 257 (а, д) (на доске и в тетрадях)

– О какой функции сегодня шла речь?

– Что является графиком функции

– В каких координатных четвертях расположен график функции?

Урок алгебры в 8-м классе “Функция у=k/х и ее график”

Цели урока:

Образовательные: сформулировать определение обратной пропорциональности, ее области определения; научить строить график функции y= k/x опираясь на свойства функции; сформировать чёткое представление о различиях свойств и расположения графика функции при различных значениях k; научить находить значение функции и аргумента по формуле У= k/x.

Развивающие: совершенствовать умения логически мыслить и выражать свои мысли вслух; стимулировать познавательную деятельность учащихся постановкой проблемного задания, оценкой и поощрением; способствовать развитию находчивости, сообразительности.

Воспитательные: воспитывать у учащихся стремление к совершенствованию своих знаний; воспитывать интерес к предмету.

Оборудование:

проектор, компьютер; раздаточный материал для устного счета.

Презентация к уроку.

План урока.

Вступительное слово учителя.

Повторение ранее изученного материала.

Изучение нового материала.

Историческая справка.

Исследование функции. Свойства графиков (работа в парах).

Обсуждение графиков (фронтальная работа).

Самостоятельная работа на построение графиков функции.

Закрепление изученного материала.

I. Актуализация опорных знаний.

(На столах учеников лежат картинки. Учитель просит показать своё настроение в начале урока)

Учитель: На уроках мы с Вами говорили о том, что весь реальный мир состоит из множества тел. Эти тела в любой момент времени взаимодействуют друг с другом на различных уровнях: химическом, физическом, информационном и т.д. (демонстрируется слайд5) Например, на уроках физики Вы изучаете “зависимость силы тока от сопротивления”, “зависимость давления газа от объема”; из жизни мы знаем о “ зависимости радиуса колеса и число совершаемых им оборотов на определенном отрезке пути” и с этой зависимостью мы встречаемся на уроках математики и т.д. Умение анализировать эти взаимодействия или зависимости сделает Вас успешными в своей деятельности!

Вы знаете, что эти величины пропорциональны

Пропорциональность – такая зависимость между величинами, при которой увеличение одной из них влечет за собой изменение во столько же раз другой величины.

Зависимость одной переменной от другой называется функцией. До сих пор Вы изучили функции y = kx + b; y = , y = x 2 . Сегодня мы продолжим изучение функций. Запишите тему урока (демонстрируется слайд 2).

2. Повторение изученного материала.

1. Как называются функции, задаваемые формулами:

а) у=2х+3; б) у = -1/2х+4; в) у=2х; г) у =-3х; д) у = х?

2. Что представляет собой их график? Как он расположен? Укажите область определения и область значения каждой из этих функций.

3. На рисунке изображен график функции у = f(x) на отрезке [- 3; 2].

Укажите наибольшее значение функции.
Укажите промежуток, в котором функция возрастает.
Найдите промежуток, в котором функция принимает отрицательные значения.

3. Изучение нового материала.

Учитель: Итак, сегодня мы изучаем функцию у =k/x .

Обратной пропорциональностью называется функция, которую можно задавать формулой вида у=k/x.

где у – зависимая переменная,

х – независимая переменная,

k – не равное нулю число.

– Областью определения функции является множество всех чисел, отличных от нуля.

– Областью значений функции является множество всех чисел, отличных от нуля.

Вопрос: Как вы считаете, глядя на аналитическую запись функции, можно сказать о том, какие значения х допустимы? (Да, х0 )

Так как выражение у =k/x имеет смысл при всех х не равных 0.

Решение задач на обратную зависимость.

Вопрос:

Как связаны между собой х и у?

Как записать каждую зависимость в виде функции?

Что общего и в чем различие этих формул?

Составить функцию, которая является обобщением рассмотренных зависимостей. (Учащиеся с помощью учителя составляют формулу)

Учитель: В явлениях природы, в человеческой деятельности часто встречаются обратно пропорциональные зависимости между двумя величинами.

Как графиком можно представить эту зависимость?

График обратно пропорциональной функции называется гипербола.

4. Историческая справка (демонстрируется слайд 10).

5. Исследование функции на примере зависимости у=12/х.

(Cоставление памятки построения графика функции)

Построение графика функции ( все учащиеся строят в своих тетрадях, один на доске).

Учитель:

определите область определения функции;

определите область значения функции;

определите промежутки убывания (возрастания) функции;

определите наибольшее (наименьшее) значение функции;

определите точку разрыва функции

Схема исследования функций.

1) Область определения функции (множество значений переменной х, при которой функция существует) или (проекция функции на ось ОХ).

2) Значения переменной х, при которой у > 0; у 20.02.2011

Гипербола. График функции и свойства.

теория по математике функции

Графиком функции у= k x . . , где k ≠ 0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.

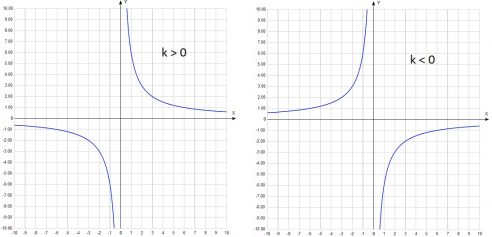
Свойства гиперболы (у= k x . )

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

Область определения – любое число, кроме нуля.
Область значения – любое число, кроме нуля.
Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у= 10 x . . .

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х	1	2	4	5	10
у

х	–1	–2	–4	–5	–10
у

Теперь делим на эти числа 10, получим значения у:

х	1	2	4	5	10
у	10	5	2,5	2	1

х	–1	–2	–4	–5	–10
у	–10	–5	–2,5	–2	–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.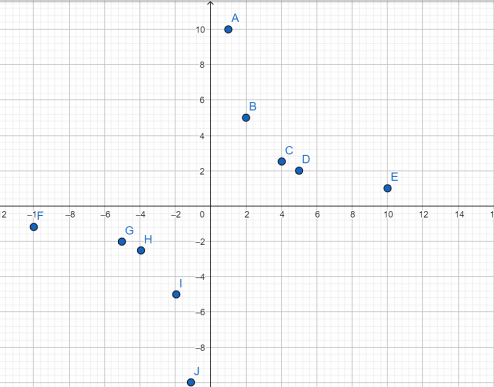

Теперь для построения гиперболы соединим точки плавной линией. 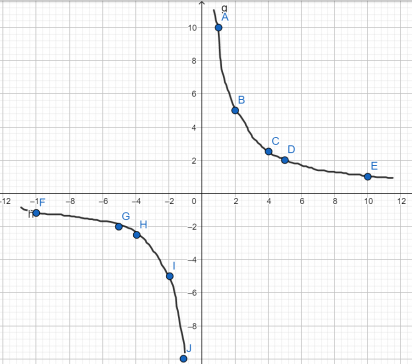Построить график функции у= − 5 x . . .

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.

х	1	2	5	10
у	–5	–2,5	–1	–0,5

х	–1	–2	–5	–10
у	5	2,5	1	0,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

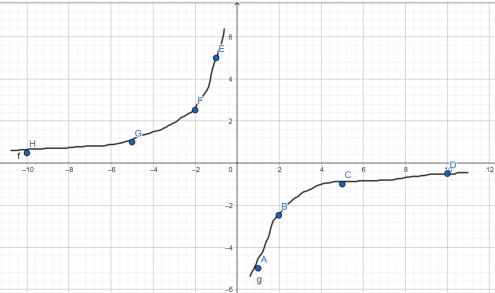
Установите соответствие между графиками функций и формулами, которые их задают.

1) y = x²

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.