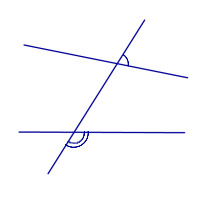
Взаимное расположение двух плоскостей в пространстве.
Признаки параллельности двух плоскостей
 Признаки параллельности плоскостей Признаки параллельности плоскостей |
Две плоскости в пространстве могут быть параллельными или могут пересекаться, как показано в следующей таблице.
| Фигура | Рисунок | Определение |
| Две пересекающиеся плоскости |  |
Две плоскости называют пересекающимися , если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия. |
| Две параллельные плоскости |  |
Две плоскости называют параллельными , если они не имеют общих точек. |


Определение:
Две плоскости называют пересекающимися , если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.


Определение:
Две плоскости называют параллельными , если они не имеют общих точек.
Признаки параллельности двух плоскостей
Первый признак параллельности двух плоскостей . Если две пересекающиеся прямые пересекающиеся прямые , лежащие в одной плоскости, соответственно параллельны параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.
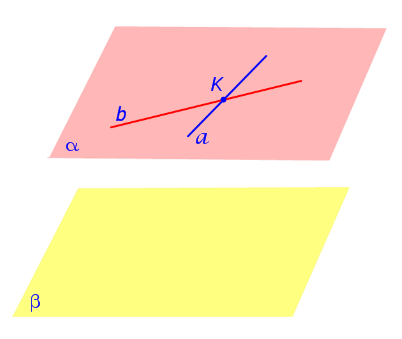
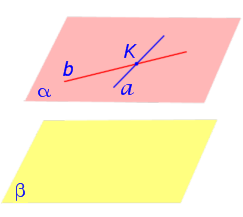
Доказательство . Рассмотрим рисунок 1, на котором изображены плоскости α и β
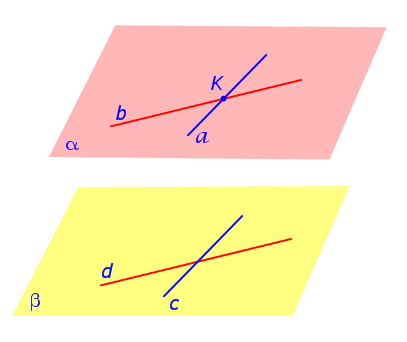
Прямые a и b лежат в плоскости α и пересекаются в точке K . Прямые c и d лежат в плоскости β и параллельны прямым a и b соответственно.
Будем доказывать первый признак параллельности двух плоскостей методом «от противного». Для этого предположим, что плоскости α и β не параллельны. Следовательно, плоскости α и β должны пересекаться, причём пересекаться по некоторой прямой. Обозначим прямую линию, по которой пересекаются плоскости α и β буквой l (рис.2) и воспользуемся признаком параллельности прямой и плоскости.
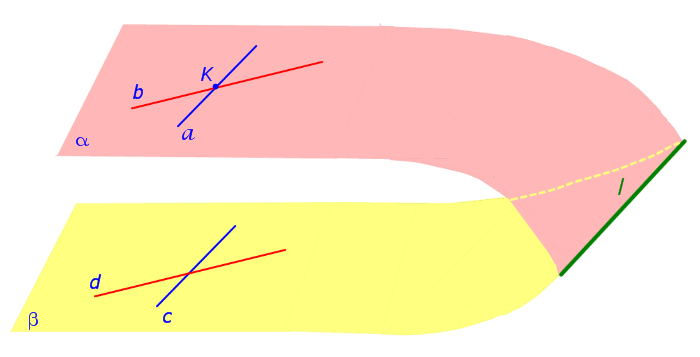
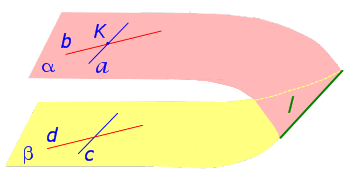
Плоскость α проходит через прямую a , параллельную прямой c , и пересекает плоскость β по прямой l . Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые a и l параллельны. В то же время плоскость α проходит через прямую b , параллельную прямой d , и пересекает плоскость β по прямой l . Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые b и l параллельны. Таким образом, мы получили, что на плоскости α через точку K проходят две прямые, а именно, прямые a и b , которые параллельны прямой l . Полученное противоречие с аксиомой о параллельных прямых аксиомой о параллельных прямых даёт возможность утверждать, что предположение о том, что плоскости α и β пересекаются, является неверным. Доказательство первого признака параллельности двух плоскостей завершено.
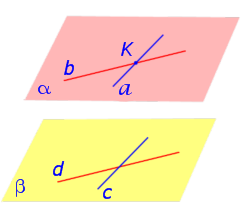
Второй признак параллельности двух плоскостей . Если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то такие плоскости параллельны.
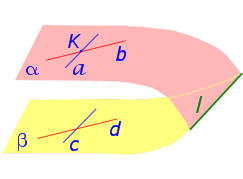
Доказательство . Рассмотрим рисунок 3, на котором изображены плоскости α и β .
На этом рисунке также изображены прямые a и b , которые лежат в плоскости α и пересекаются в точке K. По условию каждая из прямых a и b параллельна плоскости β . Требуется доказать, что плоскости α и β параллельны.
Доказательство этого утверждения аналогично доказательству первого признака параллельности двух плоскостей, и мы его оставляем читателю в качестве полезного упражнения.
Взаимное расположение двух плоскостей в пространстве — способы решения задач
Одним из важных геометрических объектов в пространстве, который часто встречается в задачах, является плоскость. Ее математическое представление позволяет решать любые практические проблемы, которые с ней связаны.

Знание взаимного расположения двух плоскостей в пространстве является необходимым условием для понимания многих геометрических задач.
Двумерный объект в пространстве
Именно таковым является любая плоскость. Чтобы понять, как она задается, следует рассмотреть два произвольных вектора, которые не лежат на одной прямой. Сумма этих векторов, каждый из которых умножается на произвольное число, задает бесконечный набор точек в пространстве. Совокупность последних однозначно определяет изучаемый объект. Этот способ построения интуитивно понятен. Математически можно записать:
(x, y, z) = (x0, y0, z0) + α *u- + β*v-.
Здесь u- и v- — это задающие плоскость векторы, α и β — произвольные рациональные числа, которые удлиняют или укорачивают исходные направленные отрезки, (x0, y0, z0) — координаты конкретной точки в пространстве, которая однозначно определяет двумерный объект из всего их параллельного набора. Любые x, y, z, которые удовлетворяют этому выражению, относятся к рассматриваемой плоскости.

Необходимо отчетливо понимать, что изучаемый геометрический объект имеет смысл рассматривать только в трехмерном пространстве, поскольку сам он является двумерным. Например, рабочая тетрадь школьников сама по себе представляет собой единственный двумерный объект.
Нормальный вектор
Направленный отрезок, который пересекает изучаемый геометрический объект под прямым углом, называется нормальным. Соответственно, прямая, параллельная нормальному вектору, будет нормалью. Этот отрезок очень важен для понимания свойств плоскостей параллельных и пересекающихся. Кроме того, с его помощью удобно задавать сам рассматриваемый геометрический объект, при этом получается уравнение общего типа.

Если известны координаты нормали, то автоматически становится понятным, какие параллельные плоскости он задает. Их бесконечное количество. Для определения единственного объекта необходимо зафиксировать точку в пространстве, например, P0 (x0, y0, z0). Пусть P (x, y, z) также принадлежит плоскому объекту, тогда векторы PP0- и n- являются перпендикулярными, где n-(A, B, C) — нормаль. Так как следствием перпендикулярности направленных отрезков является равенство нулю их скалярного произведения, то можно записать следующее равенство:
Подставляя в него известные координаты и упрощая математическое выражение, получают следующее уравнение:
A*x + B*y + C*z + D = 0, где D = -A*x0 — B*y0 — C*z0.
Это выражение называется явным, или общего типа. Оно содержит в себе координаты нормального вектора, поэтому им легко пользоваться при решении геометрических задач.
Следует также заметить, что изменение свободного члена D приведет к параллельному переносу плоскости в пространстве. Рассматриваемый объект, у которого D=0, проходит через начало координатной системы, то есть через точку (0, 0, 0).
Математические представления
Существует несколько вариантов записи уравнений изучаемого двумерного объекта. Каждым из них удобно пользоваться при решении того или иного типа задач. Основными уравнениями являются следующие:

На первый взгляд, четыре типа математических представлений рассматриваемого объекта могут показаться независимыми, однако это не так. Каждое представление с помощью несложных математических преобразований может быть переведено в любое другое.
Например, чтобы из явного представления получить векторное, необходимо сначала выразить какую-либо переменную из него. Затем представить через полученное выражение произвольную точку плоскости (x, y, z). После этого следует разложить правую часть равенства на три вектора, разделяя неизвестные переменные. Векторная форма получается путем вынесения за скобки двух неизвестных переменных и их последующей замены на параметры α и β.
Взаимное расположение плоскостей
Если исследовать несколько двумерных геометрических объектов в пространстве, то их можно расположить несколькими различными способами относительно друг друга. Существует в общем случае всего два принципиально отличающихся варианта:
- наличие пересечения;
- отсутствие пересечения.

Каждый из этих случаев взаимного расположения плоскостей требует отдельного рассмотрения. Любопытно заметить, что, в отличие от прямых в пространстве, не существует накрест лежащих двумерных объектов. Если они не пересекаются, значит, являются параллельными, и наоборот.
Изучение пересечения
Для математического рассмотрения пересечения двух плоскостей удобно воспользоваться уравнением общего типа, поскольку оно в явной форме содержит координаты нормального вектора. Пусть заданы следующие две плоскости:
- A1*x + B1*y + C1*z + D1 = 0;
- A2*x + B2*y + C2*z + D2 = 0.
Очевидно, что они будут пересекаться тогда и только тогда, когда угол между их нормалями будет отличен от нуля. Рассчитать его можно, если воспользоваться свойством скалярного произведения векторов n1- и n2-. Искомая формула имеет следующий вид:
θ = arccos (|(A1*A2 + B1*B2 + C1*C2)|/((A1 2 +B1 2 + C1 2 )^0,5* (A2 2 +B2 2 + C2 2 )^0,5)).
Следует обратить внимание, что в числителе выражения стоит знак модуля по причине того, что угол между пересекающимися плоскостями всегда является острым.
Частным случаем является пересечение рассматриваемых объектов под углом 90°. При таком варианте расположения скалярное произведение нормальных векторов будет равно нулю ((n1*n2)=0).
Под каким бы углом ни пересекались две плоскости, происходит это строго по прямой линии. Ее уравнение можно найти, если решить систему из двух общих выражений для рассматриваемых объектов. При этом направляющий вектор прямой, по которой плоскости пересекаются, определяется как векторное произведение нормалей n1- и n2-. Очевидно, что расстояние между рассматриваемыми плоскостями всегда равно нулю, независимо от угла их пересечения.
Вопрос параллельности
Если две плоскости не пересекаются, то они всегда будут параллельными друг другу. При решении геометрических задач для доказательства параллельности можно применить один из следующих способов:

Помимо этих трех способов, существует также признак параллельности плоскостей. Соответствующую теорему можно сформулировать следующим образом: если каждая из двух пересекающихся прямых одной плоскости параллельна соответствующей прямой для другой плоскости, то рассматриваемые двумерные объекты не имеют общих точек.
Для доказательства этого утверждения необходимо воспользоваться кратко свойством транзитивности: пара пересекающихся прямых однозначно задает нормаль плоскости. Поскольку они попарно параллельны, то нормали также будут параллельны друг другу.

Важным свойством параллельных плоскостей является тот факт, что пересекающие их две прямые, которые параллельны друг другу, отсекают на них отрезки одинаковой длины.
Между двумя непересекающимися двумерными объектами существует определенное расстояние, которое всегда отлично от нуля. Это утверждение следует из определения параллельных плоскостей. Вычислить его можно с помощью следующей формулы:
d = |A1*x0 + B1*y0 + C1*z0 + D1|/(A1 2 + B1 2 + C1 2 )^0,5.
Здесь (x0, y0, z0) — принадлежащая второй плоскости точка.
Решение задачи
Заданы две плоскости в пространстве следующими уравнениями:
(x, y, z) = (-1,5, 0,) + α*(-2, 1, 0) + β*(1, 0, 1).
Необходимо доказать, что оба объекта являются параллельными.
Для решения этой задачи нельзя сразу воспользоваться одним из трех способов доказательства параллельности, поскольку векторное уравнение не содержит в явной форме нормальный вектор. Чтобы его получить, необходимо векторно умножить два направляющих отрезка этой плоскости:
Для получения этого результата следует воспользоваться правилом векторного умножения в матричной форме.
В свою очередь, нормаль первой плоскости имеет координаты (1, 2, -1), то есть она совпадает с нормалью для второй плоскости. Это означает, что оба двумерных объекта являются параллельными.
Таким образом, плоскости в пространстве могут либо пересекаться, либо быть параллельными. Для выполнения условия параллельности необходимо и достаточно, чтобы их нормали не пересекались, то есть угол между ними составлял 0°.
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
Прямые и точки, размещенные в пространстве, мы будем обозначать аналогично размещенным на плоскости – с помощью строчных и прописных латинских букв ( B , A , d , q и др.) Если в условиях задачи у нас есть две точки, которые расположены на прямой, то можно выбрать такие обозначения, которые будут соответствовать друг другу, например, прямая D B и точки D и B .
Чтобы обозначить плоскость на письме, традиционно используются маленькие греческие буквы, например, α , γ или π .
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
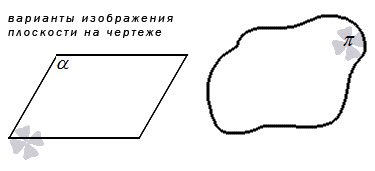
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Такой вариант расположения также называется прохождением плоскости через точку. Чтобы обозначить это на письме, используется символ ∈ . Так, если нам нужно записать в буквенном виде, что через точку A проходит некая плоскость π , то мы пишем: A ∈ π .
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Зная это правило, можно ввести новое обозначение плоскости. Вместо маленькой греческой буквы мы можем использовать названия точек, лежащих в ней, например, плоскость А В С .
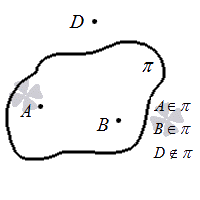
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Выше мы уже отмечали, что для обозначения плоскости в пространстве будет достаточно трех точек, а четвертая может находиться как в ней, так и вне ее. Если нужно обозначить отсутствие принадлежности точки к заданной плоскости на письме, то используется знак ∉ . Запись вида A ∉ π правильно читается как «точка A не принадлежит плоскости π »
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
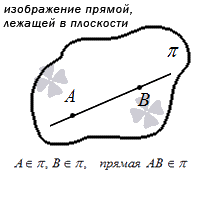
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Чтобы записать принадлежность прямой некой плоскости, используем тот же символ, что и для точки. Если мы напишем « a ∈ π », то это будет означать, что у нас есть прямая a , которая расположена в плоскости π . Изобразим это на рисунке:
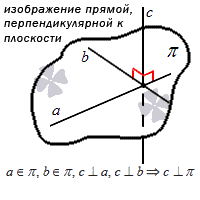
Второй вариант взаимного расположения – это когда прямая пересекает плоскость. В таком случае у них будет всего одна общая точка – точка пересечения. Для записи такого расположения в буквенном виде используем символ ∩ . Например, выражение a ∩ π = M читается как «прямая a пересекает плоскость π в некоторой точке M ». Если у нас есть точка пересечения, значит, у нас есть и угол, под которым прямая пересекает плоскость.
Графически этот вариант расположения выглядит так:
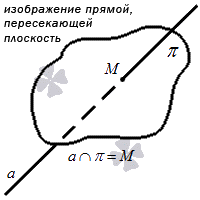
Если у нас есть две прямые, одна из которых лежит в плоскости, а другая ее пересекает, то они являются перпендикулярными друг другу. На письме это обозначается символом ⊥ . Особенности такой позиции мы рассмотрим в отдельной статье. На рисунке это расположение будет выглядеть следующим образом:
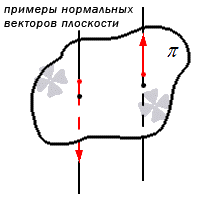
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
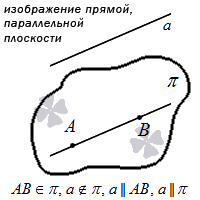
Третий случай взаимного расположения прямой и плоскости – это их параллельность. В таком случае ни одной общей точки у них нет. Для указания таких отношений на письме используется символ ∥ . Если у нас есть запись вида a ∥ π , то ее следует читать так: «прямая a является параллельной плоскости ∥ ». Подробнее этот случай мы разберем в статье про параллельные плоскости и прямые.
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
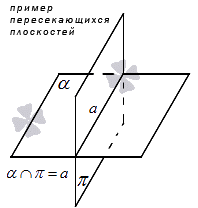
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
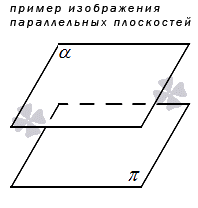
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
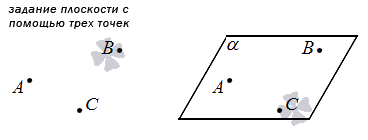
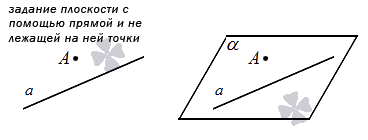
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
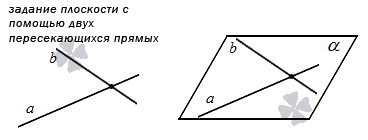
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
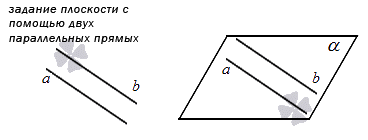
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).

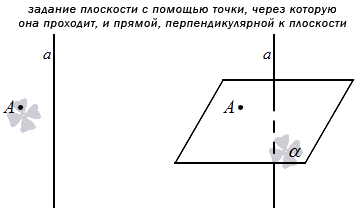
Вспомним одну теорему, изученную в рамках курса по геометрии:
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
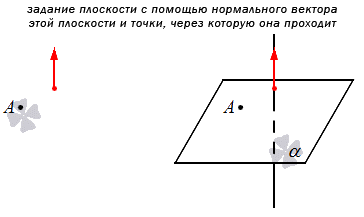
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.
Взаимное расположение плоскостей: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке
Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
Пусть две плоскости  и
и  заданы общими уравнениями
заданы общими уравнениями  и
и  .
.
Вопрос об определении угла между ними сводится к определению угла  между векторами нормалей к ним
между векторами нормалей к ним
 и
и  .
.
Из определения скалярного произведения  и из выражения в координатах длин векторов
и из выражения в координатах длин векторов  и
и  и их скалярного произведения получим
и их скалярного произведения получим

Условие параллельности плоскостей  и
и  эквивалентно условию коллинеарности векторов
эквивалентно условию коллинеарности векторов  и
и  и заключается в пропорциональности координат этих векторов:
и заключается в пропорциональности координат этих векторов:
 .
.
Условие перпендикулярности плоскостей  и
и  может быть выражено равенством нулю скалярного произведения векторов нормалей к ним
может быть выражено равенством нулю скалярного произведения векторов нормалей к ним  и
и  :
:
 .
.
Пример 1. Установить, параллельны ли две плоскости, одна из которых задана уравнением  , а другая – уравнением
, а другая – уравнением  .
.
Решение. Составим уравнения коэффициентов уравнений плоскостей:

Так как  , то коэффициенты пропорциональны, следовательно данные две плоскости параллельны.
, то коэффициенты пропорциональны, следовательно данные две плоскости параллельны.
Пример 2. Установить, перпендикулярны ли плоскости, заданные уравнениями  и
и  .
.
Решение. Плоскости перпендикулярны в том случае, когда векторы  и
и  нормалей к ним перпендикулярны и удовлетворяют условию равенства нулю их скалярного произведения. Так как
нормалей к ним перпендикулярны и удовлетворяют условию равенства нулю их скалярного произведения. Так как  , то указанное условие выполнено и, значит, данные плоскости перпендикулярны.
, то указанное условие выполнено и, значит, данные плоскости перпендикулярны.
Условие пересечения трёх плоскостей в одной точке, точка пересечения
Необходимым и достаточным условием того, что три плоскости имеют только одну общую точку (то есть, пересекаются в этой точке), является условие неравенства нулю определителя, составленного из коэффициентов уравнений:

Это условие совпадает с условием того, что система линейных уравнений имеет одно единственное решение (пройдя по ссылке можно увидеть иллюстрацию как раз на примере плоскостей).
Решение системы общих уравнений плоскостей (если оно существует и единственное) и даёт точку пересечения трёх плоскостей.
Пример 3. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:

Решение. Сначала проверим, выполняется ли условие пересечения плоскостей в одной точке. Для этого установим, отличен ли от нуля определитель системы:

Определитель отличен от нуля, следовательно система уравнений имеет единственное решение, а, значит, три плоскости пересекаются в одной точке.
Для нахождения этой точки продолжим решать систему уравнений методом Крамера. Перенесём свободные члены в правые части уравнений:

Найдём определители при неизвестных:



Нетрудно заметить, что по формулам Крамера (определитель при неизвестной делить на определитель системы) все неизвестные оказались равными единице. Таким образом, получили точку пересечения трёх плоскостей:
Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.
Пример 4. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:

Решение. Проверим, пересекаются ли плоскости в одной точке. Для этого вычислим определитель системы:

Определитель равен нулю, следовательно, данные три плоскости не пересекаются в одной точке.
Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.
Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости
Пусть даны точка  и плоскость
и плоскость  . Тогда уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости, имеет вид
. Тогда уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости, имеет вид
 .
.
Пример 5. Составить уравнение плоскости, проходящей через точку (3, -5, 1) , и параллельной плоскости  .
.
Решение. Подставляем в формулу, данную в теоретической сравке к этой главе, данные точки и другой плоскости. Получаем:

Последнее и есть искомое уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости.
Взаимное расположение плоскостей
Параллельные плоскости
Получим условия параллельности или совпадения двух плоскостей и заданных общими уравнениями:
Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей Следовательно, если плоскости (4.23) параллельны или совпадают, то т.е. существует такое число что
Плоскости совпадают, если помимо этих условий справедливо Тогда первое уравнение в (4.23) имеет вид т.е. равносильно второму, поскольку
Таким образом, плоскости (4.23) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число что но Плоскости (4.23) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: и
Условия параллельности и совпадения плоскостей (4.23) можно записать в виде
Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):
Поверхности уровня линейного четырехчлена
Поверхностью уровня функции трех переменных называется геометрическое место точек координатного пространства в которых функция принимает постоянное значение, т.е.
Для линейного четырехчлена уравнение поверхности уровня имеет вид
При любом фиксированном значении постоянной уравнение (4.24) описывает плоскость. Рассмотрим поведение семейства поверхностей уровня, отличающихся значением постоянной. Поскольку коэффициенты и не изменяются, то у всех плоскостей (4.24) будет одна и та же нормаль Следовательно, поверхности уровня линейного четырехчлена D представляют собой семейство параллельных плоскостей (рис.4.19). Поскольку нормаль совпадает с градиентом (см. пункт 3 замечаний 4.2), а градиент направлен в сторону наискорейшего возрастания функции, то при увеличении постоянной поверхности уровня (4.24) переносятся параллельно в направлении нормали.
Пересекающиеся плоскости
Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:
При этом условии система уравнений
имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).
Угол между плоскостями
Угол между двумя плоскостями можно определить как угол между их нормальными векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина угла между двумя плоскостями удовлетворяет условию
Если — нормали к плоскостям и соответственно (рис.4.20,а), то величина угла между этими плоскостями вычисляется по формуле:
Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е.
При пересечении двух плоскостей образуются четыре двугранных угла (рис.4.20). Величина двугранного угла удовлетворяет условию
получаем острый двугранный угол , образованный плоскостями (4.23), если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAOQAAAAUCAMAAACqG2GmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA2+pwDT6+X6AdLK9Qy49/usJWAwAAA2ZJREFUWMPlV9mCpCAMlDPc8P9fuxwRBNF153GHF7ujhlSlkuBx/K7FzYNd/0cgrd/bpf/qgam6LFtoAbTH73QZ5RMJXMvZrKOk1JrDmo9u+PxfJLJ9zqXPIAXQxADAp7DYSbXLpD6KyiYlDg6S2Mkek3XZnbf0kxtHlZcTsT6l7X7kAXy+JVaLboRwmpZblOAesA1m4dsQ0t63Kc7Q2+ss2U+clyjUNXoWaOKbJ2Pcgy+Q1D3rEcG4ZbuAQbOdI6UXXimqkU1k9bfNzY1j/KH+xIVXTnLKNiWjSU6L/goytKB0onyRGWCGzQeQsmMQV1le8nd3AzKsUfJaHPxSIgGyb7HZ3x0kmafmsFp8FYP2ZPEkK0/cUrdveXqWQ6fIXNR6rYGdWp1fYJoGb1SbkUUN9xCEPPbg6011446GvPwqphxftUe+d+Sn6Oy+PbHH3jCCVWaqkQayq0GWEkWVXOYi96bYm9ac+RtIl6wQAjzuJcZ2stilqhYh+CtIupCtNWKfW7bbUC+sHVZAkGdLcVJrHWrXAEXhMviyvdU7sEi7eDSUFWW9uEtJQi9JE7wcScCSpPrggUlixnApi7B60SiHUR78Eo8f3SabRWDEboRhrDSd8imTnMi8SKVKawKj6zR7AZdzCn33B5Bn6yrNlee5PQSosTQhd/Gcq15TbguSX4pe8wRLx+ay9gqza9U6ELfIFVUeGIqthdpBKmitMZQsFK/wKleckmcTHSBxSh6ldUS/zK6bXEeja/LGXVXHxPIPWbgKm3OSu4TTuqvE2XtWzgxS+Ku2Cwv6FSRg1cTGVgeJlGbVypYjot5AhhMNNNIR5JmDrEiOIOAm1cni/ZiphsTpXHeCFIShd4x27ZorSFUFlWu7YekgW6nqmBCMI/wNZD4LiNYQ+BXkmUqHTB3BPjcdJD1LIlBd1ZFq0ZVrbS3kHNypeNXlSlkX9SNIWR/M66QTQSq0J3meV6R+7a4HV/lsrnpWesJioirIcw65CaObxwfSQKIi+/lHYP+JwQ4j3kfIciCU+3NSHv3wCjI/42B8PwxVcgd9/JTNhxsXtqcyA/AwmvcgQTKmxBLKD0ByHxksJxbG3/xsD/XGMxbjT78qwSai7puaVNY/fD6bLFO7YUEVP+q7n1jiuSux1MD+k+a3rj+cGyJvT1X7swAAAABJRU5ErkJggg==” style=”vertical-align: middle;” /> (рис.4.20,а), и тупой в противном случае: (рис.4.20,б). Другими словами, по формуле (4.26) находится тот двугранный угол, образованный плоскостями, в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями. На рис.4.20 изображены пересекающиеся плоскости, положительные и отрицательные полупространства отмечены знаками + или – соответственно.
Пример 4.10. Найти величину того угла, образованного плоскостями и внутри которого лежит точка
Решение. По уравнениям плоскостей находим нормали а также величину угла между нормалями, используя (4.26):
Подставляя координаты точки в левые части уравнений плоскостей, выясняем, каким полупространствам принадлежит эта точка. Для плоскости имеем 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAN8AAAARBAMAAACvNWTbAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAYP4P3segIFPuP7ONfi1w1Fgf5QAAAqVJREFUOMtjYKA7KAAjCDBGYkMA3wMEm/0BhmZhJFl0uXcYqu3AZOa2nQdgIk1hOwNQlDC6uS6AsblcZ15AM4FRHc60SkGTE02NQBPhcfMBUUlKjnChT0pzDFDUrHzAqgFjlxZw60DtgQlVwi3kmT0FLWjmMQShhchJg0qQ13KWI4R+r0O1j+HSBjYdGPtmA5cSRJoFJrQF4UMGF1Sd/NoMh0DG8zbARJjnMvAqA+l8JFXf0EP9dQPCh5cSGCYtQLGQMQ23hXw7GIJAMcB+FBbPjIoMjCDD8qsQ6eSbFUa6MHKGsewLGCYVoFhYaobbQqCPVMCqma9+hvB5tRg4dIF0aqw3PBxbYrag2VjojZRs+VQZUCzcxYbHQnaRcKjFXy9DohlooRqQTmOw3AASBoktNWCbjqqtZyvYBRAnsc5DsZDxAMRCA6wWMp6Gp1KR4yCSDWohmAXMEQkQZaA0wigIApDY5p4FsgnijJ8LIJKSgoISQJapAdhCqCkQC8E6JSD2JMHTS+thJAsfMLDpAykhkDcfgxIXqoWMKiAL9UBMDj8QaQi2UBDIyl21WgPoBA5tHBY2OcAsXL0dGqS6YPeBLeQDBaumAb82SrhcM+BSAkYiMzgilz7gf4AcpKmhkaoJYCdjCVLedIZFsBju3gXOKIqghAqylFsPlq5UGfh1UBKakgCjJjzJhDOwPkDNh6y4Ew2TIkOTArTMyYOkIl0GXqB6dj+GlxtgqnYwmDqjaAs1YNOFFytTXJwMiLaQNZjh0AVIIj0OKyYYTEA2LcmZBs8WpTmuqNmidE8SvKBNUlJCyxY8kzRhRS+jp9IUAZRcEX1MB5INL8OETONDQTaxdyDsYG5cjJa4F/ZhqWBYiKmFuCTA5vJ+Rgg1LiCzRuOnoDYEAJ1BjPvu16j0AAAAAElFTkSuQmCC” style=”vertical-align: middle;” /> значит, точка лежит в положительном полупространстве, определяемом плоскостью Для плоскости имеем 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAMYAAAARBAMAAAB0js75AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAYQ6sm+EgQMJ68VMw0spZRHUAAAJySURBVDjLvZXNa9RAGMafzWa/SJBOD3oQlhSsiMqyUAUtKBVq/QDFr9iDCKs9KIJSxc+DotVCW3sI0kK9iEqVirisgngQS0EQW6EsiBcV6bpL17aav8HMTCbZGbrrzRySd57MvL/MM+9MgP9yfQjDHGDJLzcqbVk4qebSmlSFdXn99WAg7Nw05Eg91hwv5yQh9WJiKmhMd6sZU3OKcGnbMJDo034UhLLfPeZH/vfcxWSRRxf4YwQzT0XvM/1VP9ogpBmFkVjCZgt6N9IHhLTjsoi4ZJYRK3Ghiz8mrFQlyBAVjB5hVT9jXAv81IuYbUJ0AZmfQtoFmZFYtPSKxMhPGX/qM1JjjBEZFAavzyKTRbwZmYcB41ROYuAN9AWJ8QlGuT7j4zrulXHHz3OuAytYqnRWDNq99bAlMYDW3xLDm36pPmM46a9Hoo1Xxg2foX2heTUq7aGTkxlpR2HMsh7WcoyUIxgw23rZaI9BJf07bbUzDUk67CUhjwhhpWU+o/fzhAwSspIt62d6jx0KGS2EjBGyyotOI2DA3EJnMukx6EqMMu+20wLu5U5wRjOVzzoKI8qm0fo4ZJxgjNVedOvK9arYPfF9hdArow/3vNZaWg8V6EuSV9o3TMtedUKnem45rwYGhn511CJoUWVuAletwPxICcl5iREt4L7E0B28r7/miM0Jp/gmTnr7w0HiiW0XxfyO0mKrZbTb9nOJ8cC2x//NMPiKe19dxd4ckq7rBrX7rnNcqt2I93K+lqF5QlC7sbx7RGZE84s0l3E7ONNGR9QzLf5W2YPh1dXo6O6RmxfDc9QkVt1Rjiq8asRoafjz+Avab6T1GhuezwAAAABJRU5ErkJggg==” style=”vertical-align: middle;” /> значит, точка лежит также в положительном полупространстве, определяемом плоскостью Поскольку точка принадлежит одноименным полупространствам (положительным), то искомый угол — это угол смежный найденному углу
Пучки плоскостей
Собственным пучком плоскостей называется совокупность всех плоскостей, проходящих через фиксированную прямую ( ось пучка ).
Несобственным пучком плоскостей называется совокупность плоскостей, параллельных фиксированной плоскости (осью несобственного пучка плоскостей считается бесконечно удаленная прямая).
Любые две плоскости и определяют пучок плоскостей, содержащий заданные плоскости и Если плоскости и пересекаются, то прямая пересечения является осью собственного пучка (рис.4.21,а). Если плоскости и параллельны, то они определяют несобственный пучок параллельных плоскостей (рис.4.21,б).
Пусть заданы уравнения двух плоскостей (4.23):
Линейной комбинацией этих уравнений называется уравнение
где числа — коэффициенты линейной комбинации. Его можно записать в форме
Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю, т.е. при одновременном выполнении условий
Эти значения параметров считаются недопустимыми.
Уравнение (4.27) называется уравнением пучка плоскостей, содержащего плоскости
При любых допустимых значениях параметров уравнение (4.27) задает плоскость, принадлежащую пучку, и наоборот, для любой плоскости пучка найдутся такие значения параметров что уравнение (4.27) будет задавать эту плоскость.
Доказательство утверждения аналогично доказательству свойства пучка прямых.
Пример 4.11. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей и через точку
Решение. Искомая плоскость входит в пучок плоскостей, задаваемый уравнением (4.27)
Подставляя координаты точки получаем:
Возьмем, например, и подставим в уравнение пучка:
Итак, искомое уравнение получено.
Связки плоскостей
Собственной связкой плоскостей называется совокупность всех плоскостей, проходящих через фиксированную точку ( центр связки ).
Несобственной связкой плоскостей называется совокупность плоскостей, параллельных фиксированной прямой (центром несобственной связки плоскостей считается бесконечно удаленная точка).
Уравнение собственной связки плоскостей с центром имеет вид
где — произвольные параметры, одновременно не равные нулю.
Уравнение связки плоскостей (собственной (рис.4.22,а) или несобственной (рис.4.22,6)) можно получить в виде линейной комбинации уравнений трех плоскостей:
где — коэффициенты линейной комбинации. Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю. Эти значения параметров считаются недопустимыми.
Уравнение (4.28) называется уравнением связки плоскостей, содержащей три плоскости
При любых допустимых значениях параметров уравнение (4.28) задает плоскость, принадлежащую связке, и наоборот, для любой плоскости связки найдутся такие значения параметров что уравнение (4.28) будет задавать эту плоскость.
Доказательство утверждения аналогично доказательству свойства пучка прямых.
Взаимное расположение двух плоскостей.

Две различные плоскости в пространстве либо параллельны, либо пересекаются.
Параллельность двух плоскостей
Определение. Две плоскости в пространстве называются параллельными, если они не пересекаются.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.
Основные свойства параллельности плоскостей.
- Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
- Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны по длине.
Пересечение двух плоскостей
Две плоскости пересекаются по прямой. Общая прямая двух плоскостей называется ребром двугранного угла, образованного при пересечении данных плоскостей. При пересечении двух плоскостей образуются четыре двугранных угла. Если все они равны, то плоскости называются перпендикулярными.
Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Из признака перпендикулярности плоскостей следует, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Угол между плоскостями — наименьший из двугранных углов, образованных при пересечении плоскостей.
Угловая величина двугранного угла — это величина линейного угла данного двугранного угла.
Чтобы найти линейный угол двугранного угла надо из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру. Все линейные углы двугранного угла равны друг другу.
Тренировочные задания
Дан куб  . Найдите угол между плоскостями
. Найдите угол между плоскостями  и
и  .
.
Дан куб  . Точка
. Точка  — середина ребра
— середина ребра  . Найдите угол между плоскостями
. Найдите угол между плоскостями  и
и  .
.
В кубе  все рёбра равны
все рёбра равны  . На его ребре
. На его ребре  отмечена точка
отмечена точка  так, что
так, что  . Через точки
. Через точки  и
и  построена плоскость
построена плоскость  , параллельная прямой
, параллельная прямой  . Найдите угол наклона плоскости
. Найдите угол наклона плоскости  к плоскости грани
к плоскости грани  .
.
Дана правильная треугольная призма  , у которой сторона основания равна
, у которой сторона основания равна  , а боковое ребро равно
, а боковое ребро равно  . Через точки
. Через точки  ,
,  и середину
и середину  ребра
ребра  проведена плоскость. Найдите угол между плоскостью сечения и плоскостью ABC.
проведена плоскость. Найдите угол между плоскостью сечения и плоскостью ABC.
Все рёбра правильной треугольной призмы  имеют длину
имеют длину  . Точки
. Точки  и
и  — середины рёбер
— середины рёбер  и
и  соответственно. Найдите угол между плоскостями
соответственно. Найдите угол между плоскостями  и
и  .
.
Основанием пирамиды  является прямоугольник
является прямоугольник  , в котором
, в котором  . Диагонали прямоугольника
. Диагонали прямоугольника  пересекаются в точке
пересекаются в точке  . Отрезок
. Отрезок  является высотой пирамиды
является высотой пирамиды  . Из вершин
. Из вершин  и
и  опущены перпендикуляры
опущены перпендикуляры  и
и  на ребро
на ребро  . Найдите двугранный угол пирамиды при ребре
. Найдите двугранный угол пирамиды при ребре  , если
, если  .
.
В основании прямой призмы  лежит квадрат
лежит квадрат  со стороной
со стороной  , а высота призмы равна
, а высота призмы равна  . Точка
. Точка  лежит на диагонали
лежит на диагонали  , причём
, причём  . Найдите угол между плоскостью
. Найдите угол между плоскостью  и плоскостью
и плоскостью  .
.
Математический портал
Nav view search
Navigation
- Главная
- КОНТАКТЫ
Search
- Вы здесь:
- Home

- Аналитическая геометрия

- Взаимное расположение плоскостей, угол между плоскостями.





Взаимное расположение плоскостей, угол между плоскостями.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Условие параллельности двух плоскостей:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline
Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $overline
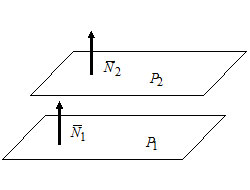
Условия перпендикулярности двух плоскостей:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline
$P_1perp P_2Leftrightarrow$ $overline

Угол между плоскостями:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline
Примеры.
В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае – косинус угла между ними.
2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$
Решение.
Вычислим угол между заданными плоскостями.
$P_1: -x+2y-z+1=0, Rightarrowoverline
$P_2: y+3z-1=0, Rightarrowoverline
Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями
Ответ: Плоскости пересекаются. $coswidehat<(P_1, P_2)>=frac<1><2sqrt<15>>.$
Решение.
Вычислим угол между заданными плоскостями.
$P_1: x-y+1=0, Rightarrowoverline
$P_2: y-z+1=0, Rightarrowoverline
Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями
Ответ: Плоскости пересекаются. $coswidehat<(P_1, P_2)>=frac<1><2>.$
2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$
Решение.
Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$
$P_1: 2x-y+5z+3=0, Rightarrowoverline
$P_2: x+3y-z-7=0, Rightarrowoverline
Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$ и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$
Ответ: $-2x+y+z+2=0.$
Домашнее задание.
В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае – косинус угла между ними.