Гиперболический синус – график функции, формулы, свойства

Гиперболические функции

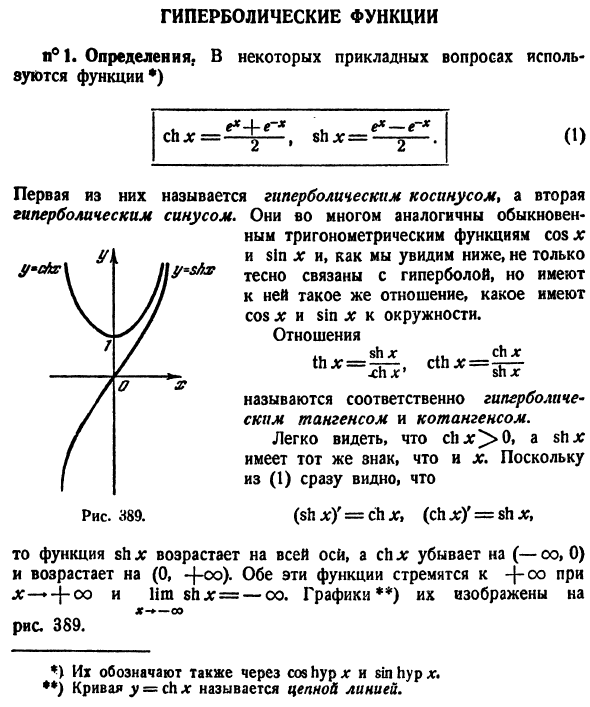
Гиперболическая функция № 1. Определение. Некоторые вопросы приложения используют функции *) e * -e-> х 0) ч * 2 ш х = Первый из них называется гиперболическим косинусом, а второй — гиперболическим синусом. Они во многом похожи на обычные тригонометрические функции cos * и sin x, и, как вы можете видеть ниже, они не только тесно связаны с гиперболой, но также потому, что cos x и sin x имеют окружность Иметь такие же отношения. связь .. sh x … ch x thx = jr, cth * = -r— xh * ‘sh x Их называют гиперболическим тангенсом и котангенсом соответственно. Легко видеть, что clue> 0 и shx имеют тот же знак, что и x.

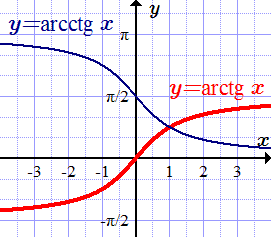
Поскольку это сразу видно из (1), (Sh x) ‘= cb x, (ch x)’ = sh x, Затем функция sh x увеличивается по оси, а ch x уменьшается при (-oo, 0) и увеличивается при (0, + oo). Обе эти функции jc-4-oo и lira shjc = -co. График **) F- ♦ -00 usLt Рисунок 389. Рисунок 389. = chA: она называется цепной линией.№ 2. Аналогия с тригонометрическими функциями. Вот несколько таких сходств:

Каждое тригонометрическое выражение имеет нечто похожее на теорию гиперболических функций. Людмила Фирмаль

1) cos’jr-f-sm * • * = 1 2) cos (* -> — y) = cos * cosy-sfn * siny, 3) 8in (jc-f-y) = sin * a «Y + sinycosjr, 4) cos (-dg) = cos x, 5) грех (-dg) = -син х, 6) cos 2x = cos * x-sin ‘x, 7) sin 2x ev 2 sin x coe dg, 8) cosO = 1, sin 0 = 0, 9) с * ^ = коэкс х-й- / грех х, 10) cosx = eXl r * i, gxi_g-си 11) sin dg = -2 / — » 12) (sin dg) ‘= cos dg, (coe dg)’ = -sin x, 13) ++ 14) = + + ! •) ch1 x-sh1 dg = 1, 2 *) ch (jc + y) = chx chy + shxsh yt 3 *) sh (jc + y) = shjcchy + shy ch Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Следовательно, вы можете определить выражения cos z и sin z для комплексного z%,

Z = xl в формуле (2) дает (учитывая P = –1) cos (xl) = —5— ”sin (xl) = -2 / — = —2— (3) Откуда cos (xl) = chsin (xl) = lshx. Уравнение (3) предоставляет ключ для создания формальной таблицы для правого столбца. Правила. Если вы пишете тригонометрическое выражение, вам нужны аргументы x, y, …. Это приводит к формуле, соответствующей исходной тригонометрической формуле в теории гиперболических функций. Пример.

Принять тригонометрическую формулу 2) cos (x — — y) = cos x cos y-sin x грешу вами cos ((* -fjf) = cos G * 0cos (yl) -sin (xl) sin (yl), что означает уравнение 2 *) h (x — — y) = h x h y- (/ w x) (i w y) = h x chu-f-sh x sh.y. Пункт 4 (В) Поскольку h * f- $ HFF = l, x% -Y = 1 из (b), который является равносторонней гиперболической линией. Поскольку p> 0 всегда, уравнение (5) является параметрическим уравнением для правой ветви гиперболы jc8-y * = 1. Так что это работает с гиперболой.

Связь с гиперболой. x = cos t, y = sin t (4) Представляет параметрическое уравнение окружности jc * — <- y * = 1. х = й, у = шт. Людмила Фирмаль

Для кругов ch t и sh t играют ту же роль, что и cos t и sin t. Указанные связи между функциями ch t и sh t и гиперболой носят несколько формальный характер. Изучите эту связь подробно. По этой причине (рис. 390) площадь кругового сектора при угле AOM = t Поскольку AOM равен, вы можете написать: Правила.

Чтобы создать стоимость и грех на рисунке, вы должны найти по кругу Точка M (xt y), где площадь сектора AOM равна y. Далее x = cos t, y = sin t. Используя похожие правила, вы можете создавать ch t и sh t. Чтобы установить это, рассмотрим точку M (X, y) на правой ветви a Рис. 390 М / JBM o A 9 Рисунок 391. Xb — y гипербола ss 1. Для ясности пусть 5> 0 (рис. 391). Найдите область F в секторе АОМ.

Это очевидно уйх. X (В) Однако y = Yx * -1. Отсюда X J F Следовательно, ^ В и формула (6) F = y Это можно сформулировать Правила. Чтобы создать на чертеже ch t и sh t, вам нужно найти гиперболу в правой ветке х% —Y = 1 Точка M (x, y), где площадь сектора AOM равна y. Тогда x = ch y = eh t. На самом деле, * сила (7) y = yln (lg + y), То есть х + у = е *. Однако X * — / = 1, т. Е. (Π-Qy) y) к I, тогда y) = 1 и x-y = e к *. Из уравнения jc-j-> y = q-y = Замечания. На рисунке 390 не только площадь сектора AOM равна y, но угол AOM также равен t. Разумеется, угол на фиг.391 АОМ не равен t ♦).

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Гиперболические функции

Содержание:

Гиперболические функции

Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Основные понятия:

Рассмотрим единичную окружность с центром в начале координат, уравнение которого имеет вид х 2 + у 2 = 1.

Согласно определению, синусом угла называют ординату у точки А(х, у) единичной окружности, а косинусом — абсциссу х этой же точки (рис. 1)

Докажем, что площадь сектора АОВ равна числовому значению угла AOD, взятом в радианах.

Действительно, если R=1, а угол сектора АОВ- то

Следовательно, в тригонометрических функциях за аргумент можно принимать не только угол, а и площадь соответствующего сектора.

Рассмотрим теперь равнобокую гиперболу с асимптотами , уравнение которой имеет вид

Повторим предыдущие рассуждения:

– выберем на гиперболе т. А(х, у);

– проведём радиусы ОА и ОВ ().

Образовавшуюся фигуру OANB называют гиперболическим сектором (сектором ),

абсциссу точки А – гиперболическим косинусом;

ординату точки А – гиперболическим синусом.

Возьмём за аргумент площадь гиперболического сектора . Получим:

Найдём площадь гиперболического сектора, как разность площади треугольника АОВ и криволинейной трапеции ANB.

Потому, что фигура симметрична, имеем

либо, решив систему

Аналогично как в тригонометрии вводят понятия тангенса и котангенса

Свойства гиперболических функций

Чётность и нечётность проверим подставив (-х) в соответствующие формулы

Следовательно, как и в тригонометрических функциях, имеем чётная, а нечётные.

Остальные свойства легко установить построив графики гиперболических функций.

Для построения воспользуемся записью

то есть графики функций

Полученные графическим сложением ординат графики функций имеют вид:

Графики следующие

Видим, что в отличии от тригонометрических, гиперболические функции непериодические. Основные свойства каждой из гиперболических функций указаны в опорном конспекте (п. 10.5).

Дифференцирование и интегрирование гиперболических функций

Гиперболические функции можно дифференцировать и интегрировать. Выведем формулы производных и интегралов.

Переход от гиперболических функций к тригонометрическим и наоборот

Используя гиперболические функции можно вывести формулы Эйлера. Действительно, вспомним разложение в ряд Маклорена функций

Положим в разложении функции у=е х за аргумент х=zj. Получим:

Учитывая, что где будем иметь:

Именно эти формулы позволяют установить зависимость между тригонометрическими и гиперболическими функциями.

Принимаем без доказательств, что все тригонометрические формулы действительны и для воображаемого аргумента. Это предположение позволит установить зависимость между гиперболическими функциями.

Аналогично можно получить формулы для

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

курсовая работа по алгебре на тему “Гиперболические функции”

в данной работе представлен материал, что собой представляют гиперболические функции и область их применения

Скачать:

Вложение	Размер
kursovaya.docx	478.77 КБ

Предварительный просмотр:

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Алтайский государственный педагогический университет»

Институт физико-математического образования

Кафедра алгебры и методики обучения математике

Выполнила студентка 3512з группы

Латкина Наталья Сергеевна

(подпись) Научный руководитель:

«____» __________________ 2018г.

Председатель ГАК ______________

Глава 1 Гиперболические функции их свойства и применение……….……. 5

1.1Понятие гиперболические функции. Гиперболический синус его

1.2Определение гиперболического косинуса и его важнейшие свойства…..11

1.3Определение гиперболического тангенса его свойства и график………..14

1.4 Определение гиперболического котангенса и его свойства……………. 18

1.5 Применение гиперболических функций при вычислении интегралов….20

Первое появление гиперболических функций историки обнаружили в трудах английского математика Абрахама де Муавра (1707- 1722).

Независимое открытие и дальнейшее исследование свойств гиперболических функций было проведено Иоганном Ламбертом (1768), который установил широкий параллелизм формул обычной и гиперболической тригонометрии. Н. И. Лобачевский впоследствии использовал этот параллелизм, пытаясь доказать непротиворечивость неевклидовой геометрии, в которой обычная тригонометрия заменяется на гиперболическую.

Современное определение и обстоятельное их исследование выполнил Винсент Риккати в 1757 году («Opusculorum», том I), он же предложил их обозначения: sh, ch. Риккати исходил из рассмотрения единичной гиперболы

Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы.

Современная математика рассматривает гиперболические функции, как пары экспоненциальной функции, но Риккати исследовал их свойства, используя только геометрические свойства гиперболы х² — y² =1 или 2xy =1. Он использовал геометрические методы, хотя он был знаком с работами Эйлера, предшествовавших выходу книги Риккати.

Над гиперболическими функциями Риккати работал вместе с Джироламо Саладини. Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.

Для достижения цели необходимо решить следующие задачи:

1.Изучить литературу и раскрыть понятие о гиперболических функциях.

2.Рассмотреть все виды функций изучить их основные свойства и графики.

3. Рассмотреть использование гиперболических функций при интегрировании обыкновенных дифференциальных уравнений.

4.Научиться применять гиперболические функции при вычислении интегралов.

Глава 1 Гиперболические функции их свойства и применение

1.1 Понятие гиперболические функции. Гиперболический синус его свойства и применение»

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Гиперболические функции задаются следующими формулами:

Ввиду соотношения =1 гиперболические функции дают параметрическое представление гиперболы x 2 − y 2 = 1 (x=cht,y=sht). При этом аргумент t = 2S , где S — площадь криволинейного треугольника, взятая со знаком «+», если сектор лежит выше оси OX, и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом

Основные свойства гиперболического синуса.

Гиперболическим синусом называется
; – ∞ ∞,-∞

Если в тождестве (1) произвести замену x на ix , то получим

1.Область определения: D(y) = (-∞;+x).

2. Множество значений: E(y) = (-x;+∞).

3. Четность и нечетность: нечётная.

4. Периодичность: не периодическая.

5. Нули функции: x=0.

6. Промежутки знакопостоянства: функция отрицательна для xϵ(-x;+0), положительна – для xϵ(0;+ ∞).

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция возрастает для всех xϵ(-∞;+∞)

9. Точки пересечения с осями координат : (0,0).

10. Асимптоты: асимптот не имеет.

11. График функции изображен на рисунке 1.

Доказательство. Если провести замену аргумента (х) на (-х), то получим

Что доказывает нечетность функции sh (x)

(3) Данные формулы могут быть выведены следующим образом. Из определения имеем:

Перемножая отдельно левые и правые части этих тождеств, составим следующие выражения:

Теперь легко найти, что

таким образом формула сложения проверена.

Формула двойного угла:

Доказательство: 2 chxshx =

Формула (4) доказана.

Формула понижения степени:

Пример применения формулы понижения степени:

Вычислить, используя формулу понижения степени:

Понизить степень выражения

Решение: применим формулу понижения степени для синуса , получим

Вычислить интеграл
Решение.
Так как
, то интеграл

Решение.
По определению,
. Подставляя это в интеграл, получаем

Разложение в степенные ряды.

Гиперболический синус аналитичен во всей комплексной плоскости, за исключением существенно особой точки на бесконечности.

Примеры решения задач:

Найти приближенное значения sh2

Решение: По определению,
подставляем значение x= 2, получим

В последнее выражение подставим значение экспоненты e 2,75:

1.2 Определение гиперболического косинуса и его важнейшие свойства

Определение: Гиперболическим косинусом называется функция

Если в тождестве (11) произвести замену (х) на (ix), то получим

1. Область определения : D(y)=(-∞;x).

2 .Множество значений: E(y)=[1;+∞).

3. Четность и нечетность : чётная.

4. Периодичность : не периодическая.

5. Нули функции : нулей не имеет.

6. Промежутки знакопостоянства : функция положительна для xϵ(-x;+x).

7. Наибольшее и наименьшее значения : наименьшее значение, равное 1 , функция принимает при x=0.

8. Промежутки возрастания и убывания : функция убывает при xϵ(-x;0); возрастает – при xϵ(0;+∞). 9. Точки пересечения с осями координат : пересекает ось Oy в точке y=1 , ось Ox не пересекает.

10. Асимптоты : асимптот не имеет 11. График функции изображен на рисунке 2.

Важные свойства гиперболического косинуса

Формула сложения: ch(x+y)=ch(x)+sh(x)∙sh(y) (14) Данная формула сложения выводится следующим образом. Из определения имеем:

Перемножая, отдельно левые и правые части этих тождеств, составим выражение:

Далее получаем следующее:

Таким образом формула сложения гиперболического косинуса проверена.

Формула двойного угла:

Для того, чтобы доказать формулу(13) заменим в формуле (12) y на x.

Ch(x+y)=ch(x)∙ch(y)+sh(x)∙sh(y), получаем, что

Формула понижения степени:

1.3Определение гиперболического тангенса его свойства и график

Гиперболический тангенс определяются через отношение гиперболического синус и косинуса.

Гиперболическим тангенсом называется функция

Основные свойства гиперболического тангенса.

1. Область определения : D(y) = (-∞;+x).

2. Множество значений : E(y) = (-1;1).

3. Четность и нечетность : нечётная.

4. Периодичность : не периодическая.

5. Нули функции : x=0.

6. Промежутки знакопостоянства : функция отрицательна для xϵ(-∞;0); положительна – для xϵ(0;+∞).

7. Наибольшее и наименьшее значения : наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания : функция возрастает для xϵ(-x;+x).

9. Точки пересечения с осями координат : (0;0).

10. Асимптоты : имеет горизонтальные асимптоты y=-1 и y=1 .

11. График функции изображен на рисунке 3.

Важные свойства и их доказательства

Свойство чётности th(-x)=-th(x) (19)

Доказательство . Если провести замену аргумента (х) на (-х), то получим

Доказали, что функция нечётная.

Произведение тангенсов гиперболических

Формула суммы(разности) тангенсов гиперболических

Формула двойного угла

Производная тангенса гиперболического

Разложение в степенные ряды.

Примеры решения задач:

Задание 1: Вычислить интеграл

Решение: Представим тангенс гиперболический в виде

Задание 2: Найти приближенное значение th 2

Пользуясь определением гиперболического тангенса

Решение , можно записать, что

1.4 Определение гиперболического котангенса и его свойства

Гиперболическим котангенсом называется функция

1. Область определения : D(y) = (-x ; 0) ᴗ (0;+∞).

2. Множество значений : E(y) = (-∞;-1) ᴗ (1; +x).

3. Четность и нечетность : нечётная.

4. Периодичность : не периодическая.

5. Нули функции : нулей не имеет.

6. Промежутки знакопостоянства : функция отрицательна для xϵ(-x;0); положительна – для xϵ(0;+∞).

7. Наибольшее и наименьшее значения : наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания : функция убывает для xϵ D(y).

9. Точки пересечения с осями координат : нет.

10. Асимптоты : имеет горизонтальные асимптоты y=-1 и y=1.

11. График функции изображен на рисунке 4

Некоторые важные свойства гиперболического котангенса

Свойство чётности: cth(-x)= ctx(x)

Доказательство: Если провести замену аргумента (х) на (-х), то получим

Тем самым мы доказали нечётность функции.

Разложение в степенной ряд

1.5 Применение гиперболических функций при вычислении

Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.

Наиболее важные формулы дифференцирования и интегрирования гиперболических функций имеют вид:

Приведем еще несколько полезных соотношений:

Если подынтегральное выражение содержит гиперболическую функцию, то такой интеграл можно свести к интегрированию рациональной функции с помощью подстановки.

Решение. Сделаем подстановку u = 2 + 3sh x, du = 3ch xdx . Тогда. Следовательно, интеграл равен

Поскольку, , и, следовательно,

, интеграл можно переписать в виде

Делая замену u = ch x, du = sh xdx, получаем

Используем интегрирование по частям: . Пусть u=x, dv=sh xdx .Тогда . В результате находим интеграл

Пример 4: Вычислить интеграл .

Решение. Так как , то интеграл равен

Пример 5: Найти интеграл.

Решение. По определению, .

Подставляя это в интеграл, получаем

Пример 6: Найти интеграл .

Решение. По определению, и . Следовательно, Сделаем замену u = e x , du = e x dx и вычислим искомый интеграл.

Решение. Интегрируем по частям. Полагаем

Интеграл принимает вид

Применим интегрирование по частям еще раз. Теперь полагаем

Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто вычисляются с помощью замен переменных с использованием гиперболических функций.

В рамках данного исследования мы рассмотрели основные гиперболические функции и их применение.

Были достигнуты следующие цели:

1) Была изучена и систематизирована литература;

2) На основании изученной литературы были выделены определения гиперболических функций;

Рассмотрены примеры решения задач на определение производных гиперболических функций;

Было рассмотрено применение гиперболических функций при вычислении интегралов.

Таким образом, решая задачи, можно сделать вывод о значимости гиперболических функций в математическом анализе. Они необходимы для более простого дифференцирования функций.

1. Аксенов, А.П. Математический анализ в 4 ч. часть 1. учебник и практикум для академического бакалавриата / А.П. Аксенов. — Люберцы: Юрайт, 2016. — 282 c. 2. Аксенов, А.П. Математический анализ в 4 ч. часть 4. учебник и практикум для академического бакалавриата / А.П. Аксенов. — Люберцы: Юрайт, 2016. — 406 c.
3. Баврин, И.И. Математический анализ 2-е изд., испр. и доп. учебник и практикум для спо / И.И. Баврин. — Люберцы: Юрайт, 2016. — 327 c.
4. Баврин, И.И. Математический анализ для педагогических вузов 2-е изд., испр. и доп. учебник и практикум для прикладного бакалавриата / И.И. Баврин. — Люберцы: Юрайт, 2016. — 327 c.
5. Балдин, К.В. Математический анализ: Учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев… — М.: Флинта, МПСУ, 2013. — 368 c.
6. Боярчук, А.К. Справочное пособие по высшей математике. Т. 3. Часть 2: Математический анализ: кратные и криволинейные интегралы / А.К. Боярчук, И.И. Ляшко, Я.Г. Гай. — М.: ЛИБРОКОМ, 2012. — 256 c.
7. Будаев, В.Д. Математический анализ. Функции одной переменной: Учебник / В.Д. Будаев, М.Я. Якубсон… — СПб.: Лань, 2012. — 544 c.
8. Будаев, В.Д. Математический анализ. Функции одной переменной: Учебник / В.Д. Будаев, М.Я. Якубсон. — СПб.: Лань, 2012. — 544 c.
9. Бутузов, В., Ф. Математический анализ в вопросах и задачах. 6-е изд., испр / В.Ф. Бутузов, Г.Н. Крутицкая и др… — СПб.: Лань, 2008. — 480 c.
10. Гаврилов, В.И. Математический анализ: Учебное пособие для студентов учреждений высшего профессионального образования / В.И. Гаврилов, Ю.Н. Макаров, В.Г. Чирский. — М.: ИЦ Академия, 2013. — 336 c.
11. Горлач, Б.А. Математический анализ: Учебное пособие / Б.А. Горлач… — СПб.: Лань, 2013. — 308 c.
12. Горлач, Б.А. Математический анализ / Б.А. Горлач. — СПб.: Лань, 2013. — 608 c.
13. Злобина, С.В. Математический анализ в задачах и упражнениях / С.В. Злобина, Л.Н. Посицельская. — М.: Физматлит, 2009. — 360 c.
14. Зорич, В.А Математический анализ. Часть 1 (6-е изд.) / В.А Зорич. — М.: МЦНМО, 2012. — 702 c.— 818 c.
15. Ивлев, В.В. Математический анализ. Функции многих переменных / В.В. Ивлев. — М.: Изд. ИКАР, 2013. — 548 c.
16. Ильин, В.А. Математический анализ ч. 2 3-е изд. учебник для бакалавров / В.А. Ильин, В.А. Садовничий, Б.Х. Сендов. — Люберцы: Юрайт, 2016. — 357 c.
17. Карташев, А.П. Математический анализ. 2-е изд., стер / А.П. Карташев, Б.Л. Рождественский. — СПб.: Лань, 2007. — 448 c.
18. Киркинский, А.С. Математический анализ: Учебное пособие для ВУЗов / А.С. Киркинский. — М.: Академический проект, 2006. — 526 c.
19. Кытманов, А.М. Математический анализ. учебное пособие для бакалавров / А.М. Кытманов. — Люберцы: Юрайт, 2016. — 607 c.
20. Лейнартас, Е.К. Математический анализ: Учебное пособие для бакалавров / А.М. Кытманов, Е.К. Лейнартас, В.Н. Лукин; Под ред. А.М. Кытманов. — М.: Юрайт, 2012. — 607 c.
21. Ляшко, И.И. Антидемидович. Т.3. Ч.1. Справочное пособие по высшей математике. Математический анализ: интегралы, зависящие от параметра / И.И. Ляшко, А.К. Боярчук, Я.Г. Гай, Г.П. Головач. — М.: Ленанд, 2016. — 160 c.
22. Солодовников, А.С. Математика в экономике: учебник. Ч.2. Математический анализ. 3-е изд., доп. и перер / А.С. Солодовников и др… — М.: Финансы и статистика, 2011. — 560 c.
23. Шершнев, В.Г. Математический анализ: сборник задач с решениями: Учебное пособие / В.Г. Шершнев. — М.: НИЦ ИНФРА-М, 2013. — 164 c.
24. Шипачев, В.С. Математический анализ. Теория и практика. / В.С. Шипачев. — М.: Высшая школа, 2009. — 350 c.
25. Шубин, М.А. Математический анализ для решения физических задач / М.А. Шубин. — М.: МЦНМО, 2003. — 40 c.

Математика

In the coming weeks, this wiki’s URL will be migrated to the primary fandom.com domain. Read more here

Deutsch
English
Español
Suomi
Français
Italiano
日本語
한국어
Português
Türkçe
中文

Гиперболические функции

История
Обсуждение (0)

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Содержание

1 Определение
- 1.1 Геометрическое определение
2 Свойства
- 2.1 Связь с тригонометрическими функциями
- 2.2 Важные тождества
- 2.3 Разложение в степенные ряды
- 2.4 Графики
- 2.5 Аналитические свойства
3 Обратные гиперболические функции
4 История
5 Применение
6 Ссылки

Определение

Определение гиперболических функций через гиперболу

Один из способов определения тригонометрических функций через единичную окружность

Гиперболические функции задаются следующими формулами:

гиперболический синус:

(в зарубежной литературе обозначается )

Существует сленговые названия: «шинус», «шимус»(?). Однако их использование не научно.

гиперболический косинус:

(в зарубежной литературе обозначается )

Существует сленговые названия: «чосинус», «кошинус». Однако их использование не научно.

гиперболический тангенс:

(в зарубежной литературе обозначается ).

Существует сленговые названия: «щангенс», «тахинус». Однако их использование не научно.

Иногда также определяются

гиперболический котангенс:

Существует сленговые названия: «кочангенс», «кохинус». Однако их использование не научно.

гиперболические секанс и косеканс:

, .

Геометрическое определение

Ввиду соотношения гиперболические функции дают параметрическое представление гиперболы (, ). При этом аргумент , где — площадь криволинейного треугольника , взятая со знаком «+», если сектор лежит выше оси , и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.

Свойства

Связь с тригонометрическими функциями

Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

Важные тождества

Чётность :
Формулы сложения:
Формулы двойного угла:

Производные:
Интегралы:

Разложение в степенные ряды

Здесь — числа Бернулли.

Графики

Аналитические свойства

Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках , где — целое. Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек , вычеты его в этих полюсах также равны единице.

Обратные гиперболические функции

Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь».

— обратный гиперболический синус: — обратный гиперболический косинус — обратный гиперболический тангенс — обратный гиперболический котангенс — обратный гиперболический секанс 0end>right.>” /> — обратный гиперболический косеканс

Эти функции имеют следующее разложение в ряд:

1>” />

История

Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы.

Дальнейшее исследование свойств гиперболических функций было проведено Ламбертом .

Риккати применял для гиперболических функций обозначения и . В дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой. Например, в Энциклопедии Брокгауза и Эфрона используются обозначения , , в русскоязычной литературе закрепились обозначения , в англоязычной закрепились , .

Применение

Аналогично тому, как матрицы вида описывают повороты двумерного евклидова пространства, матрицы описывают повороты в простейшем двумерном пространстве Минковского . В связи с этим гиперболические функции часто встречаются в теории относительности .

Однородная веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции (в связи с чем график гиперболического косинуса иногда называют цепной линией ). Это обстоятельство используется при проектировании арок , поскольку форма арки в виде перевёрнутой цепной линии наиболее удачно распределяет нагрузку.

Ссылки

GonioLab: Интерактивная демонстрация тригонометрических и гиперболических функций на Java Web Start
История гиперболических функций (англ)
БСЭ: Знаки математические
Биография Риккати (англ.)
http://ru.wikipedia.org/wiki/Гиперболические_функции

cs:Hyperbolická funkce he:פונקציות היפרבוליות hu:Hiperbolikus függvények is:Breiðbogafall nl:Hyperbolische functie pl:Funkcje hiperboliczne sr:Хиперболичне функције sv:Hyperbolisk funktion

43. Показательные и логарифмические выражения. Показательная функция, гиперболические функции

Показательной функцией Называется функция

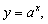где

Основные свойства показательной функции

1. Область определения:

2. Множество значений:

3. Четность и нечетность: не обладает свойством четности.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: Функция положительна для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: если 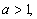функция возрастает для всех если – убывает для

9. Точки пересечения с осями координат: пересекает ось Оу в точке ось Ох не пересекает.

10. Асимптоты: прямая Y = 0 (ось Ох) является горизонтальной асимптотой.

11. График функции для A > 1 изображен на рис. 6.1, для 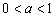– на рис. 6.2.

Из свойств функции следует: неравенство равносильно неравенствам:

1) если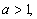

2) если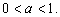

Показательная функция с основанием Е, где Е – иррациональное число Е = 2,718281…, называется Экспонентой, пишут или

Через показательные выражения с основанием Е определяются Гиперболические функции.

Гиперболическим синусом называется функция

Основные свойства гиперболического синуса

1. Область определения:

2. Множество значений: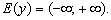

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции:

6. Промежутки знакопостоянства: Функция отрицательна для положительна – для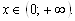

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция возрастает для всех

9. Точки пересечения с осями координат:

10. Асимптоты: асимптот не имеет.

11. График функции изображен на рис. 6.3.

Гиперболическим косинусом называется функция

Основные свойства гиперболического косинуса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: четная.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: Функция положительна для

7. Наибольшее и наименьшее значения: наименьшее значение, равное 1, функция принимает при

8. Промежутки возрастания и убывания: функция убывает при возрастает при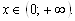

9. Точки пересечения с осями координат: пересекает ось Оу в точке ось Ох не пересекает.

10. Асимптоты: асимптот не имеет.

11. График функции изображен на рис. 6.4.

Гиперболические тангенс и котангенс определяются через отношение гиперболических синуса и косинуса.

Гиперболическим тангенсом Называется функция

т. е.

Основные свойства гиперболического тангенса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции:

6. Промежутки знакопостоянства: Функция отрицательна для положительна для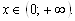

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция возрастает для

9. Точки пересечения с осями координат:

10. Асимптоты: имеет горизонтальные асимптоты и

11. График функции изображен на рис. 6.5.

Гиперболический котангенсом называется функция

т. е.

Основные свойства гиперболического котангенса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: Функция отрицательна для положительна для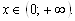

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция убывает для

9. Точки пересечения с осями координат: нет.

10. Асимптоты: имеет горизонтальные асимптоты и

11. График функции изображен на рис. 6.6.

Пример 1. Сравнить числа:

1) и 2) и

3) и

Решение. 1) Преобразуем числа к одному основанию:

Так как и функция монотонно возрастает, то следовательно,

2) Преобразуем числа:

Так как и функция монотонно убывает, то следовательно,

3) Преобразуем числа:

Так как и функция монотонно возрастает, то тогда и

Пример 2. Построить график функции:

1) 2)

Решение. 1) Строим график функции

График функции получаем из предыдущего путем смещения его на 3 единицы влево по оси Ох и на 4 единицы вниз по оси Оу.

Для построения графика заданной функции оставляем ту часть графика функции которая лежит над осью Ох и на оси Ох. Ту часть графика, которая расположена ниже оси Ох, отображаем в верхнюю полуплоскость симметрично относительно оси Ох (рис. 6.7).

2) Строим график функции (см. рис. 6.5).

График функции получаем из предыдущего путем смещения его на 2 единицы вниз вдоль оси Оу.

Для построения графика заданной функции оставляем ту часть графика функции которая лежит правее оси Оу и на оси Оу. Часть графика, которая лежит левее оси Оу, отбрасываем, а оставшуюся часть отображаем в левую полуплоскость симметрично оси Оу (рис. 6.8).

Пример 3. Доказать тождество

Решение.

Графики гиперболических функций

Определение гиперболических синусов, косинусов, тангенсов и котангенсов

Графики гиперболических функций

Свойства

Связь (сумма)

Чётность

Разность квадратов

Формулы суммы и разности аргументов

Формулы произведений гиперболического синуса и косинуса

Формулы суммы и разности гиперболических функций

Формулы производных

Формулы интегралов

Формулы неравенства

Формулы разложения в степенные ряды

Появление названия «гиперболическая функция»

Применение гиперболических функций.

Введение

Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы 1 .
Современная математика рассматривает гиперболические функции, как пары экспоненциальной функции, но Риккати исследовал их свойства, используя только геометрические свойства гиперболы х² — y² = 1 или 2xy = 1. Он использовал геометрические методы, хотя он был знаком с работами Эйлера, предшествовавших выходу книги Риккати.
Над гиперболическими функциями Риккати работал вместе с Джироламо Саладини. Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.

Цель данной работы – изучить гиперболические функции и их применение.

Определения гиперболических синусов, косинусов, тангенсов и котангенсов

Гиперболическим синусом называется функция:

Гиперболическим косинусом называется функция:

Гиперболическим тангенсом называется функция:

Гиперболическим котангенсом называется функция:

Гиперболическим секансом и косекансом называется функции:

Графики гиперболических функций

Рисунок 1- график гиперболического синуса y = sh x

Рисунок 2- график гиперболического косинуса y = ch x

Рисунок 3- график гиперболической функции тангенсаy = th x

Рисунок 4- график гиперболической функции котангенса y = cth x

Свойства

Связь (сумма)

sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = – i cth z
th iz = i tg z ; cth iz = – i ctg z
Здесь i – мнимая единица, i 2 = –1.

Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.

Чётность

sh(–x) = – sh x; ch(–x) = ch x.
th(–x) = – th x; cth(–x) = – cth x.

Функция ch(x) – четная. Функции sh(x), th(x), cth(x) – нечетные.

Разность квадратов

ch 2 x – sh 2 x = 1.

Гиперболический котангенс cth(x), формулы и примеры

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы.

Дальнейшее исследование свойств гиперболических функций было проведено Ламбертом. Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.

Производные гиперболических функций легко находятся, поскольку гиперболические функции являются комбинациями Например, гиперболические синус и косинус определяются как Производные этих функций имеют вид Гиперболические функции задаются следующими формулами: 1)гиперболический синус: (в зарубежной литературе обозначается sinx); 2)гиперболический косинус: (в зарубежной литературе обозначается cosx); 3)гиперболический тангенс: (в зарубежной литературе обозначается tanx); 4)гиперболический котангенс: ; 5)гиперболические секанс и косеканс: Геометрическое определение: Ввиду соотношения гиперболические функции дают параметрическое представление гиперболы При этом аргумент t=2S , где S — площадь криволинейного треугольника OQR , взятая со знаком «+», если сектор лежит выше оси OX , и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом. Связь с тригонометрическими функциями: Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента. Аналитические свойства: Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности.

Гиперболический тангенс аналитичен везде, кроме полюсов в точках , где n — целое. Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек вычеты его в этих полюсах также равны единице.

Таблица производной.
Ответ:

Таблица производных (которые в основном нам нужны):

46)Производная функции – заданной параметрически.

Пусть задана зависимость двух переменных x и y от параметра t, изменяющегося в пределах от Пусть функция имеет обратную: Тогда мы можем, взяв композицию функций получить зависимость y от x: Зависимость величины y от величины x, заданной параметрически, можно выразить через производные функций поскольку и, по формуле производной обратной функции, где — значение параметра, при котором получается интересующее нас при вычислении производной значение x. Заметим, что применение формулы приводит нас к зависимости между снова выраженной в виде параметрической зависимости: второе из этих соотношений — то же, что участвовало в параметрическом задании функции y(x) . Несмотря на то, что производная не выражена через в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра t. Покажем это на следующем примере. Пример 4.22: Пусть зависимость между x и y задана параметрически следующими формулами: Найдём уравнение касательной к графику зависимости y(x) в точке Значения получаются, если взять t=1. Найдём производные x и y по параметру t: Поэтому При t=1 получаем значение производной это значение задаёт угловой коэффициент k искомой касательной. Координаты точки касания заданы в условии задачи. Значит, уравнение касательной таково: Заметим, что исходя из полученной параметрической зависимости мы можем отыскать вторую производную функции y по переменной x:

Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.

Определения гиперболических функций, их области определений и значений

sh x — гиперболический синус

Графики гиперболических функций

График гиперболического синуса y = sh x
График гиперболического косинуса y = ch x
График гиперболического тангенса y = th x
График гиперболического котангенса y = cth x

Формулы с гиперболическими функциями

Связь с тригонометрическими функциями

sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = — i cth z
th iz = i tg z ; cth iz = — i ctg z
Здесь i — мнимая единица, i 2 = -1 .

Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.

Четность

sh(-x) = — sh x ; ch(-x) = ch x .
th(-x) = — th x ; cth(-x) = — cth x .

Функция ch(x) — четная. Функции sh(x) , th(x) , cth(x) — нечетные.

Разность квадратов

ch 2 x — sh 2 x = 1 .

Формулы суммы и разности аргументов

sh(x ± y) = sh x ch y ± ch x sh y
,
ch(x ± y) = ch x ch y ± sh x sh y
,
,
,

sh 2
x = 2 sh x ch x
,
ch 2
x = ch 2 x + sh 2 x
= 2 ch 2 x — 1 = 1 + 2 sh 2 x
,
.