Что такое синус (sin) – определение, график, свойства

• 0 при x = π n
• 1 при x = π /2 + 2π n
• -1 при x = -π /2 + 2π n

Во всех случаях n принадлежит Z

Овладение базовыми функциями углов необходимо для всех, кто собирается заниматься математикой и смежными с ней дисциплинами, такими как инженерия, топография и так далее. Чтобы закрепить изученный материал, рекомендуем посмотреть видео ниже и проверить полученные знания с помощью тестовых заданий.

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).

Синус (sin) угла поворота

Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y

Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х

Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x

Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Синус и косинус определены для любых углов α .

Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )

Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )

При решении практических примеров не говорят “синус угла поворота α “. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности – точка A c координатами ( 1 , 0 ).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Функция y = sin x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).

Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x синусоидой .
Часть синусоиды для 0≤x≤2π называют волной синусоиды .
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды .

п.2. Свойства функции y=sinx⁡

1. Область определения (xinmathbb) – множество действительных чисел.

2. Функция ограничена сверху и снизу

Область значений (yin[-1;1])

3. Функция нечётная

4. Функция периодическая с периодом 2π

5. Максимальные значения (y_=1) достигаются в точках

Минимальные значения (y_=-1) достигаются в точках

Нули функции (y_<0>=sinx_0=0) достигаются в точках (x_0=pi k)

6. Функция возрастает на отрезках

$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$

Функция убывает на отрезках

$$ fracpi2+2pi kleq xleqfrac<3pi><2>+2pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:

a) (left[fracpi6; frac<3pi><4>right]) $$ y_=sinleft(fracpi6right)=frac12, y_=sinleft(fracpi2right)=1 $$ б) (left[frac<5pi><6>; frac<5pi><3>right]) $$ y_=sinleft(frac<3pi><2>right)=-1, y_=sinleft(frac<5pi><6>right)=frac12 $$

Пример 2. Решите уравнение графически:
a) (sinx=3x)

Один корень: x = 0

б) (sinx=2x-2pi)

Один корень: x = π

в) (sinx-sqrt=0)
(sinx=sqrt)

Один корень: x = π

г*) (sinx=left(x-fracpi2right)^2-frac<4>)
(y=left(x-fracpi2right)^2-frac<4>) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -frac<4>right)) (см. §29 справочника для 8 класса)

Два корня: (x_1=0, x_2=pi)

Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$

(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) – исходная функция поднимается вверх на 2. Область значений (yin[1;3]).

Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac <2>$$

Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) – период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac<2>) – период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Тригонометрия в прямоугольном треугольнике

• Тригонометрический круг

• Основное тригонометрическое тождество

• Таблица значений тригонометрических функций

• Градусы и радианы

• Формулы приведения

• Теорема синусов

• Расширенная теорема синусов

• Теорема косинусов

• Тригонометрические уравнения (10-11 класс)

• Примеры решений заданий из ОГЭ

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Тригонометрия: Таблица значений тригонометрических функций

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

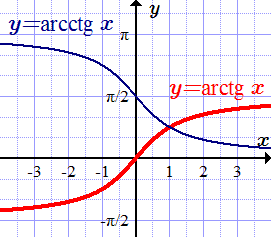
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Что такое синус

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такие СИНУС.

Наверняка многие знают, что это понятие относится к математике. Все мы учились в школе и проходили тригонометрию.

С понятиями СИНУС, КОСИНУС, ТАНГЕНС и КОТАНГЕНС школьники знакомятся в 8 классе.

И сейчас без этих знаний не обойтись на ЕГЭ. И задачки по тригонометрии обязательно входят в программу тестов единого государственного экзамена.

Так что эта статья будет в первую очередь полезна старшеклассникам. А читателям более старшего возраста будет полезно лишний раз освежить давно забытые знания.

Что такое тригонометрия

Но давайте начнем совсем с азов. Раз уж мы сказали, что СИНУС – это некая тригонометрическая функция, давайте расскажем и что такое тригонометрия.

Тригонометрия – это раздел математики, который был основан еще в Древней Греции. Само слово состоит из двух половин «τρίγωνον» и «μετρέω», что можно дословно перевести как «изучение треугольников».

Впервые нечто похожее на тригонометрические функции появилось в Древней Греции. Во всяком случае, их можно отследить по трудам Евклида и Архимеда, то есть в III веке до нашей эры.

Хотя ученые не исключают, что похожими вычислениями пользовались и при строительстве Египетских пирамид. А это уже 2-2,5 тысячи лет до нашей эры.

И опять же, пирамиды ведь имеют треугольную форму (в плоскости). И тригонометрия связана напрямую с треугольниками. Возможно совпадение, а возможно и нет.

Правда, в тригонометрии рассматривают конкретные треугольники – прямоугольные. Напомним, это такие фигуры, у которых две стороны из трех пересекаются друг с другом под углом 90 градусов.

Выглядит такой треугольник вот так:

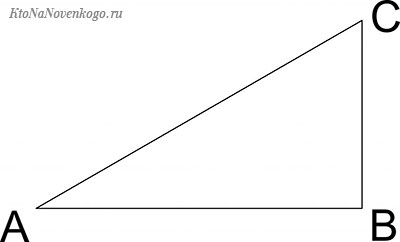
У такого треугольника стороны имеют определенные названия:

КАТЕТЫ – это стороны, которые пересекаются под прямым углом.

В нашем случае это стороны АВ и ВС. Это название также имеет древнегреческие корни. Так, слово «káthetos» переводится как «перпендикуляр, опущенный, ответственный».

ГИПОТЕНУЗА – сторона, которая идет под наклоном и соединяет между собой два катета.

В нашем случае это отрезок АС. Слово также родом из Древней Греции, «ὑποτείνουσα» означает «натянутая». И это очень хорошо характеризует этот отрезок, ведь он действительно выглядит как натянутая струна между двух опор. И даже если перевернуть треугольник, это ощущение не изменится.

Синус — это .

А вот теперь мы подобрались к самому главному, определению СИНУСА. Это величина не существует сама по себе. Она имеет отношение к какому-то углу треугольника. А конкретно к углам α (альфа) и β (бета), которые наглядно показаны на следующем рисунке.

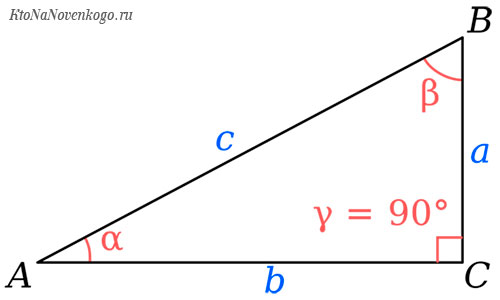
А вот теперь долгожданное определение:

СИНУС угла – это отношение противолежащего катета к гипотенузе.

Чтобы было понятно, о чем речь, взгляните еще раз на наш рисунок прямоугольного треугольника. В данном случае, противолежащим катетом к углу α будет сторона ВС. А противолежащим катетом к углу β будет сторона АС.

Соответственно, катет ВС для угла α будет прилежащим. И точно таким же будет катет ВС для угла β.

Конкретные формулы синусов будут такими:

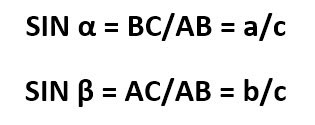
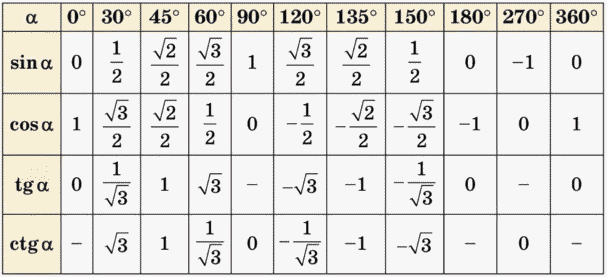
Значения синусов

Чаще всего школьники имеют дело с определенными углами. Например, 30, 45, 60, 90 градусов и так далее. И чтобы не высчитывать каждый раз значение тригонометрических функций через стороны треугольника, есть уже готовые таблицы:

1. 0 градусов — SIN = 0;
2. 30 градусов — SIN = ½;
3. 45 градусов — SIN = √2/2;
4. 60 градусов – SIN = √3/2;
5. 90 градусов – SIN = 1;
6. 180 градусов – SIN = 0;
7. 270 градусов – SIN = -1;
8. 360 градусов – SIN = 0.

Вместо заключения

СИНУС – это не единственная тригонометрическая функция, которую проходят в школе. Есть еще и другие, и все они также связаны с прямоугольным треугольником.

А называются они вот так:

КОСИНУС – это обратная синусу величина (даже в переводе с латыни это слово означает «перевернутый синус»). Косинус равен отношению прилежащего катета к гипотенузе.

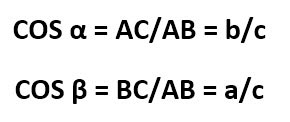
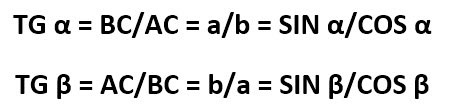
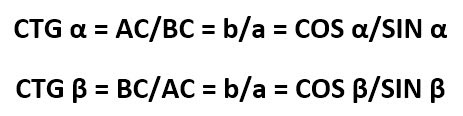
Вот и все, что мы хотели рассказать о тригонометрической функции СИНУС.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

Вот я вроде школу давно окончил, а вот все равно помню все. Потому что учили нас на совесть, а не спустя рукава. Вот скажите мне, а где в школах есть такое, что если ученик не понял, то учитель был готов потратить на него субботу и воскресенье чтобы объяснить дополнительно? Именно поэтому даже ярые троешники что-то знали.

Сейчас если ты в школе не понял, то все. Я дочери сам объяснял все по синусам, хотя и не учитель вообще. И кстати в современных учебниках материал очень плохо подан. Качаю старые советские, там куда понятнее. У вас кстати в статье хорошо рассказано. Я кстати в свое время так и запоминал, что это противоположный катет к гипотенузе.

Вспомнить никогда не будет лишним. Согласна с вами, Владимир, учили нам на совесть, спасибо нашим учителям.

«Соответственно, катет ВС для угла α будет прилежащим.»

Ошибка, для угла α прилежащим будет катет AC!

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №4. Свойства и график функции .

Перечень вопросов, рассматриваемых в теме

• Изучение свойств графика функции ;
• Определение промежутков монотонности, наибольшего и наименьшего значения, нулей функции ;
• Определение свойств и положение графика тригонометрических функций вида и
• Построение графика функции
• Объяснять зависимость свойств и положения графика функции вида иот значения коэффициентов а, k, b;
• Демонстрирование уверенного владения свойствами функции .

Глоссарий по теме

Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции , где a≠0.

Число │a│ называется амплитудой.

Основная литература:

Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

На прошлом уроке мы говорили о свойствах графика косинуса:

1) область определения функции – множество R всех действительных чисел;

2) Множество значений функции – отрезок [–1;1];

3) Функция косинуса периодическая, ;

4) Функция чётная;

5) Функция принимает:

• значение, равное 0, при ;
• наименьшее значение, равное –1, при

;

• наибольшее значение, равное 1, при ;

6) Функция

• возрастает на отрезке и на отрезках, получаемых сдвигами этого интервала на .

Давайте сравним их со свойствами графика синуса, а для начала определим следующие моменты:

• При движении точки до первой четверти ордината увеличивается;
• При движении точки по второй четверти ордината постепенно уменьшается;
• Функция возрастает на отрезке и убывает на отрезке .

Свойства функции :

3) Период функции равен ;

4) Функция чётная/нечётная;

5) Функция принимает:

• значение, равное 0, при ;
• наименьшее значение, равное –1, при ;
• наибольшее значение, равное 1, при ;
• положительные значения на интервале (0;) и на интервалах, получаемых сдвигами этого интервала на ;
• отрицательные значения на интервале и на интервалах, получаемых сдвигами этого интервала на .

6) Функция

• возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на ;
• убывает на отрезке и на отрезках, получаемых сдвигами этого отрезка на .

Изменяя амплитуду и значение аргумента функции синуса график ведет себя следующим образом (рис.1)

Рис. 1 – графики синуса

Сдвиг графика влево/вправо вдоль оси абсцисс

Если к аргументу функции добавляется постоянная, то происходит сдвиг (параллельный перенос) графика вдоль оси Ох.

Правило:
1) чтобы построить график функции , нужно сдвинуть график вдоль оси Ох на b единиц влево;

2) чтобы построить график функции , нужно график сдвинуть вдоль оси ОХ на b единиц вправо.

Теоретический материал для самостоятельного изучения

1. На следующие утверждения нужно ответить верно/неверно.

1) Тригонометрическая функция определена на всей числовой прямой.

2) График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.

3) График тригонометрической функции можно построить, используя одну главную полуволну.

Ответ: верно, неверно, верно.

2. Вспомним, что мы уже знаем о функции , ответив на вопросы:

1) Какие значения может принимать переменная х. Какова область определения этой функции?

2) В каком промежутке заключены значения выражения . Назови наибольшее и наименьшее значения функции .

3) Функция синуса чётная или нечётная?

Примеры и разборы решения заданий тренировочного модуля:

Пример 1. Найдем все корни уравнения , принадлежащие отрезку .

Построим графики функций и (рис. 6)

Рис. 7 – графики функций и .

Графики пересекаются в четырёх точках, абсциссы которых являются корнями уравнения . На выбранном отрезке от корни уравнения симметричны: и . Из рисунка видно, что симметричность корней объясняется периодичностью функции: аналогично для

Ответ: ; .

Пример 2.Найти все решения неравенства , принадлежащие отрезку .

Из рисунка 7 видно, что график функции лежит выше графика функции на промежутках и и

Ответ: , ,

Синус, косинус, тангенс и котангенс (ЕГЭ 2022)

Понятия синуса, косинуса, тангенса, котангенса неразрывно связаны с понятием угла.

Звучит ужасно, да?

Не так страшен черт, как его малюют!

Чтобы хорошо разобраться в этих понятиях (нет, не в чёрте! в тригонометрии ), начнём с самого начала.

Синус, косинус, тангенс, котангенс — коротко о главном.

Синус угла — это отношение противолежащего (дальнего) катета к гипотенузе

Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе

Тангенс угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому)

Котангенс угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему).

Понятие угла: радиан, градус

Давай для начала разберёмся в понятии угла.

Посмотрим на рисунок.

Вектор ( AB) «повернулся» относительно точки ( A) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол ( alpha ).

Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!

Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.

Углом в ( 1<>^circ ) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную ( frac<1><360>) части окружности.

Таким образом, вся окружность состоит из ( 360) «кусочков» круговых дуг. То есть угол, описываемый окружностью, равен ( 360<>^circ ).

То есть на рисунке выше изображён угол ( beta ), равный ( 50<>^circ ), то есть этот угол опирается на круговую дугу размером ( frac<50><360>) длины окружности.

Углом в ( 1) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.

Ну что, разобрался? Если нет, то давай разбираться по рисунку.

Итак, на рисунке изображён угол ( gamma ), равный ( 1) радиану.

То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина ( AB) равна длине ( BB’) или радиус ( r) равен длине дуги ( l)).

Таким образом, длина дуги вычисляется по формуле:

( l=theta cdot r), где ( theta ) — центральный угол в радианах.

Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?

Да, для этого надо вспомнить формулу длины окружности. Вот она:

Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен ( 2pi ).

То есть, соотнеся величину в градусах и радианах, получаем, что ( 2pi =360<>^circ ).

Соответственно, ( pi =180<>^circ ).

Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.

А сколько радиан составляют ( 60<>^circ )?

Уловил? Тогда вперёд закреплять:

Тогда смотри ответы:

Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике

Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?

Давай разбираться. Для этого нам поможет прямоугольный треугольник.

Как называются стороны прямоугольного треугольника?

Всё верно, гипотенуза и катеты.

Гипотенуза — это сторона, которая лежит напротив прямого угла (в нашем примере это сторона ( AC))

Катеты – это две оставшиеся стороны ( AB) и ( BC) (те, что прилегают к прямому углу).

Причём, если рассматривать катеты относительно угла ( angle BAC), то катет ( AB) – это прилежащий катет, а катет ( BC) — противолежащий.

Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?

Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.

В нашем треугольнике ( sin beta =frac).

Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.

В нашем треугольнике ( cos beta =frac).

Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

В нашем треугольнике ( tgbeta =frac).

Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).

В нашем треугольнике ( ctgbeta =frac).

Эти определения необходимо запомнить!

Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.

А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:

В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).

Тогда убедись, посмотрев на рисунок:

Рассмотрим, к примеру, косинус угла ( beta ).

По определению, из треугольника ( ABC): ( cos beta =frac=frac<4><6>=frac<2><3>).

Но ведь мы можем вычислить косинус угла ( beta ) и из треугольника ( AHI): ( cos beta =frac=frac<6><9>=frac<2><3>).

Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.

Если разобрался в определениях, то вперёд закреплять их!

Для треугольника ( ABC), изображённого ниже на рисунке, найдём ( sin alpha , cos alpha , tg alpha , ctg alpha ).

Тогда пробуй сам: посчитай то же самое для угла ( beta ).

Ответы: ( sin beta =0,6; cos beta =0,8; tg beta =0,75; ctg beta =frac<4><3>).

Единичная (тригонометрическая) окружность

Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным ( 1).

Такая окружность называется единичной. Еще ее называют тригонометрической. Это одно и тоже.

Эта окружность — универсальная шпаргалка для решения уравнений и даже неравенств, если уметь ей пользоваться!

У нас есть целая статья, посвященная ей, которая так и называется «Тригонометрическая (единичная) окружность».

Здесь мы тоже ее разберем довольно подробно.

Как можно заметить, данная окружность построена в декартовой системе координат.

Радиус окружности равен единице.

При этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси ( x) (в нашем примере, это радиус ( AB)).

Каждой точке окружности соответствуют два числа: координата по оси ( x) и координата по оси ( y).

А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме?

Для этого надо вспомнить про рассмотренный прямоугольный треугольник.

На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника.

Рассмотрим треугольник ( ACG). Он прямоугольный, так как ( CG) является перпендикуляром к оси ( x).

Чему равен ( cos alpha ) из треугольника ( ACG)?

Всё верно ( cos alpha =frac).

Кроме того, нам ведь известно, что ( AC) – это радиус единичной окружности, а значит, ( AC=1).

Подставим это значение в нашу формулу для косинуса. Вот что получается:

А чему равен ( sin alpha ) из треугольника ( ACG)?

Ну конечно, ( sin alpha =frac)!

Подставим значение радиуса ( AC) в эту формулу и получим:

Так, а можешь сказать, какие координаты имеет точка ( C), принадлежащая окружности? Ну что, никак?

А если сообразить, что ( cos alpha ) и ( sin alpha ) — это просто числа?

Какой координате соответствует ( cos alpha )?

Ну, конечно, координате ( x)!

А какой координате соответствует ( sin alpha )?

Всё верно, координате ( y)!

Таким образом, точка ( C(x;y)=C(cos alpha ;sin alpha )).

А чему тогда равны ( tg alpha ) и ( ctg alpha )?

Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что ( tg alpha =frac=frac), а ( ctg alpha =frac=frac).

А что, если угол будет больше ( 90<>^circ =frac<2>)?

Вот, к примеру, как на этом рисунке:

Что же изменилось в данном примере?

Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику.

Чему равно значение синуса, косинуса, тангенса и котангенса для угла ( <_<1>><_<1>>G=180<>^circ -beta )?

Всё верно, придерживаемся соответствующих определений тригонометрических функций:

Ну вот, как видишь, значение синуса угла всё так же соответствует координате ( y); значение косинуса угла – координате ( x); а значения тангенса и котангенса соответствующим соотношениям.

Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.

Уже упоминалось, что начальное положение радиус-вектора – вдоль положительного направления оси ( x).

До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке?

Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным.

Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные.

Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет ( 360<>^circ ) или ( 2pi ).

А можно повернуть радиус-вектор на ( 390<>^circ ) или на ( -1140<>^circ )?

Ну конечно, можно!

В первом случае, ( 390<>^circ =360<>^circ +30<>^circ ), таким образом, радиус-вектор совершит один полный оборот и остановится в положении ( 30<>^circ ) или ( frac<6>).

Во втором случае, ( -1140<>^circ =-360<>^circ cdot 3-60<>^circ ), то есть радиус-вектор совершит три полных оборота и остановится в положении ( -60<>^circ ) или ( -frac<3>).

Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на ( 360<>^circ cdot m) или ( 2pi cdot m) (где ( m) – любое целое число), соответствуют одному и тому же положению радиус-вектора.

Ниже на рисунке изображён угол ( beta =-60<>^circ ).

Это же изображение соответствует углу ( -420<>^circ ,-780<>^circ , 300<>^circ ,660<>^circ ) и т.д.

Этот список можно продолжить до бесконечности.

Все эти углы можно записать общей формулой ( beta +360<>^circ cdot m) или ( beta +2pi cdot m) (где ( m) – любое целое число)

Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:

Вот тебе в помощь единичная окружность:

Возникли трудности? Тогда давай разбираться.

Итак, мы знаем, что:

Отсюда мы определяем координаты точек, соответствующих определённым мерам угла.

Ну что же, начнём по порядку: углу в ( 90<>^circ =frac<2>) соответствует точка с координатами ( left( 0;1 right)), следовательно:

( text 90<>^circ =frac=frac<1><0>Rightarrow text 90<>^circ ) — не существует;

Дальше, придерживаясь той же логики, выясняем, что углам в ( 180<>^circ , 270<>^circ , 360<>^circ , 450<>^circ (=360<>^circ +90<>^circ ) ) соответствуют точки с координатами ( left( -1;0 right),text< >left( 0;-1 right),text< >left( 1;0 right),text< >left( 0;1 right)), соответственно.

Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.

Ответы:

( displaystyle sin 180<>^circ =sin pi =0) ( displaystyle cos 180<>^circ =cos pi =-1) ( text 180<>^circ =text pi =frac<0><-1>=0)

( text 180<>^circ =text pi =frac<-1><0>Rightarrow text pi ) — не существует

( sin 270<>^circ =-1) ( cos 270<>^circ =0)

( text 270<>^circ =frac<-1><0>Rightarrow text 270<>^circ ) — не существует

( text 270<>^circ =frac<0><-1>=0) ( sin 360<>^circ =0) ( cos 360<>^circ =1) ( text 360<>^circ =frac<0><1>=0)

( text 360<>^circ =frac<1><0>Rightarrow text 2pi ) — не существует

( sin 450<>^circ =sin left( 360<>^circ +90<>^circ right)=sin 90<>^circ =1) ( cos 450<>^circ =cos left( 360<>^circ +90<>^circ right)=cos 90<>^circ =0)

( text 450<>^circ =text left( 360<>^circ +90<>^circ right)=text 90<>^circ =frac<1><0>Rightarrow text 450<>^circ ) — не существует

( text 450<>^circ =textleft( 360<>^circ +90<>^circ right)=text 90<>^circ =frac<0><1>=0).

Таким образом, мы можем составить следующую табличку:

Нет необходимости помнить все эти значения!

Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:

А вот значения тригонометрических функций углов в ( 30<>^circ =frac<6>, 45<>^circ =frac<4>) и ( 30<>^circ =frac<6>, 45<>^circ =frac<4>), приведённых ниже в таблице, необходимо запомнить:

Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений: