Число сочетаний – свойства, формулы и примеры решения

Сочетания

п.1. Сочетания без повторений

Например:
Из 10 программистов нужно отобрать 4 для участия в проекте. Сколькими способами это можно сделать?
$$mathrm< n = 10, k=4 >$$ В данном случае, порядок отбора не важен (выборка неупорядоченная); каждый кандидат может войти только один раз в выборку (выборка без повторений). Поэтому рассматриваем неупорядоченные 〈10,4〉 –выборки без повторений. Количество способов отбора равно: $$mathrm< C_<10>^4=frac<10!><6! 4!>=frac<10cdot 9cdot 8cdot 7><1cdot 2cdot 3cdot 4>=210 >$$ Ответ: 210.

п.2. Сочетания с повторениями

Например:
Нужно отобрать 4 программистов для участия в проекте. Многочисленных претендентов можно разделить на две категории: желающих работать удаленно и предпочитающих работу в офисе. Сколько всего комбинаций из любителей офиса и удалёнки может оказаться в выбранной четвёрке? $$mathrm< n = 2, k=4 >$$ Порядок отбора не важен; кандидатов из каждой категории может быть несколько или ни одного. Поэтому рассматриваем неупорядоченные 〈2,4〉 –выборки с повторениями: $$ mathrm< overline_2^4=frac<(2+4-1)!><(2-1)4!>=frac<5!><4!>=5 > $$ Всего – 5 комбинаций: OOOO,OOOD,OODD,ODDD,DDDD
где O – любитель офиса; D – любитель удалёнки. Напоминаем, что порядок не важен – важен только состав группы.
Ответ: 5.

п.3. Биномиальные коэффициенты и их свойства

Подробно о биноме – см. §28 справочника для 7 класса.
Для n-й степени бинома справедливо выражение: $$ mathrm< (apm b)^n=a^n+C_n^1a^bpm C_n^2a^b^2+. +C_n^b^n > $$ где (mathrm) – биномиальные коэффициенты, к оторые одновременно являются количествами сочетаний без повторений из n по k: $$ mathrm< C_n^k=frac <(n-k)!k!>> $$ Таким образом, биномиальные коэффициенты можно определять как с помощью треугольника Паскаля, так и с помощью данной формулы.
Заметим, что в литературе также часто встречается обозначение (mathrm) для биномиальных коэффициентов (mathrm).

Свойства биномиальных коэффициентов

Свойство симметрии

Свойство Паскаля

Замена индексов

Вынесение за скобки

Рекуррентные формулы

Свойство суммы

Свойство разности

Свойства максимума

Если n – четное, то максимальное значение (mathrm) имеет при (mathrm<2>>).
Если n – нечетное, то максимальное значение имеют два коэффициента (mathrm), при (mathrm<2>>) и (mathrm<2>>)

Свёртка Вандермонда

Сумма квадратов

Взвешенное суммирование

Связь с числами Фибоначчи

п.4. Примеры

Пример 1. На столе лежит 10 яблок и 5 груш.
1) Сколькими способами можно выбрать 7 фруктов?
2) Сколькими способами можно выбрать 7 фруктов, чтобы среди них было 3 груши?

1) Всего у нас n = 10 + 5 = 15 фруктов. Нужно выбрать k = 7 фруктов.
Порядок выбора не важен, т.е. выборка неупорядоченная. Находим: $$ mathrm< C_n^k=C_<15>^7=frac<15cdot 14cdot 13cdot 12cdot 11cdot 10cdot 9><1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7>=6435 > $$ Существует 6435 способов выбрать 7 фруктов из 15.

2) Выбираем 4 яблока из 10 и 3 груши из 5.
Для яблок: $$ mathrm< C_<10>^4=frac<10cdot 9cdot 8cdot 7><1cdot 2cdot 3cdot 4>=210 > $$ Для груш: $$ mathrm< C_3^5=C_<5>^2=frac<5cdot 4><1cdot 2>=10 > $$ По правилу произведения, общее количество способов выбрать 4 яблока и 3 груши: $$ mathrm< C_<10>^3cdot C_<5>^3=210cdot 10=2100 > $$ Ответ: 1) 6435; 2) 2100.

Пример 2. В кондитерском магазине продаётся 4 вида пирожных. Сколькими способами можно купить 7 пирожных? $$ mathrm < n=4, k=7 >$$ Порядок выбора пирожных неважен – выборка неупорядоченная; пирожные одного вида могут повторяться. Значит, находим количество сочетаний с повторениями: $$ mathrm< overline_4^7=C_<7+4-1>^7=C_<10>^7=C_<10>^3=frac<10cdot 9cdot 8><1cdot 2cdot 3>=120 > $$ Ответ: 120

Пример 3. Рота состоит из 3 офицеров, 6 сержантов и 15 рядовых. Сколькими способами можно выбрать из них отряд, состоящий из 1 офицера, 2 сержантов и 5 рядовых?

По всем трём множествам делаем неупорядоченную выборку (т.е., сочетания) без повторений.
Выбираем офицеров: (mathrm)
Выбираем сержантов: (mathrm<1cdot 2>=15>)
Выбираем рядовых: (mathrm^6=frac<15cdot 14cdot 13cdot 12cdot 11><1cdot 2cdot 3cdot 4cdot 5>=3003>)
По правилу произведения, отряд можно выбрать:
(mathrm<3cdot 15cdot 3003=135135>) способами.
Ответ: 135135.

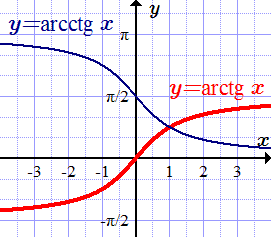
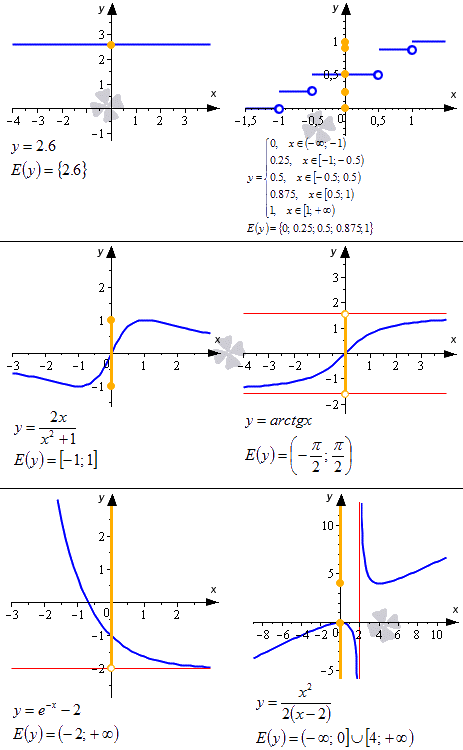
Пример 5. Рассчитайте все (mathrm^k>) по рекуррентной формуле (mathrm^k=fracC_n^>).
Постройте график (mathrm^k(k)>). Сделайте выводы.

Начальное значение (mathrm^0=1>).

1.3.3. Сочетания

В учебниках обычно даётся лаконичное и не очень понятное определение сочетаний, поэтому в моих устах формулировка будет не особо рациональной, но, надеюсь, доходчивой:

Сочетаниями называют различные комбинации из 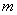объектов, которые выбраны из множества 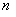различных объектов, и которые отличаются друг от друга хотя бы одним объектом. Иными словами, отдельно взятое сочетание – это уникальная выборка из 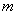элементов, в которой не важен их порядок (расположение). Общее же количество таких уникальных сочетаний рассчитывается по формуле .
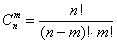Задача 3

В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Решение: прежде всего, обращаю внимание на то, что по логике такого условия, детали считаются различными – даже если они на самом деле однотипны и визуально одинаковы (в этом случае их можно, например, пронумеровать
).

В задаче речь идёт о выборке из четырёх деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество:

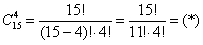(прерываю решение для промежуточных объяснений)

И здесь, конечно, не нужно «тягать» значения 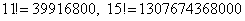. В похожей ситуации я советую использовать следующий приём: в знаменателе выбираем наибольший факториал (в данном случае 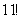) и сокращаем на него дробь. Для этого числитель следует представить в виде 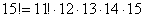. Распишу очень подробно:

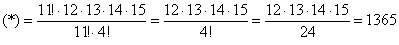способами можно взять 4 детали из ящика.

Ещё раз: что это значит? Это значит, что из 15 различных деталей можно составить одну тысячу триста шестьдесят пять уникальных сочетаний из 4 деталей. То есть, каждая такая комбинация из четырёх деталей будет отличаться от других комбинаций хотя бы одной деталью.

Ответ: 1365 способами

Формуле 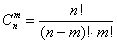необходимо уделить самое пристальное внимание, поскольку она является «хитом» комбинаторики. При этом полезно понимать и без всяких вычислений записывать «крайние» значения: 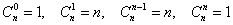. Применительно к разобранной задаче:

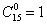– единственным способом можно не выбрать ни одной детали;
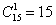способами можно взять 1 деталь (любую из 15);
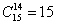способами можно взять 14 деталей (при этом какая-то одна из 15 останется в ящике);
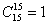– единственным способом можно выбрать все пятнадцать деталей.

Рекомендую вновь обратиться к Приложению Формулы комбинаторики и внимательно ознакомиться с биномом Ньютона и треугольником Паскаля (пункт 3), по которому очень удобно выполнять проверку вычислений количества сочетаний 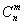при небольших значениях «эн».

Для самостоятельного решения:

Задача 4

а) Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

б) В шахматном турнире участвует 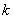человек и каждый с каждым играет по одной партии. Сколько всего партий сыграно в турнире?

Чем приятны многие комбинаторные задачи, так это краткостью – главное, разобраться в сути. Решения и ответы в конце книги.

Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №31. Сочетания без повторений. Бином Ньютона

Перечень вопросов, рассматриваемых в теме

1) понятие сочетания без повторения и их свойства;

2) правила подсчета числа сочетаний из n-элементов по m без повторений;

3) бином Ньютона;

4) треугольник Паскаля.

Глоссарий по теме

Сочетаниями из n элементов по m в каждом (m ≤ n) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.

Число всевозможных сочетаний из n различных элементов по m элементов обозначают

Формула для подсчёта числа сочетаний:

Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.

Числа являются коэффициентами в формуле бинома Ньютона:

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Общим термином «соединения» в комбинаторике называют три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству. Ранее уже рассматривались два вида комбинаций. Это перестановки и размещения. В данных соединениях важен порядок размещения элементов. В случае, когда этот порядок не важен, то мы имеем дело с сочетаниями.

Сочетаниями из n элементов по m в каждом (m ≤ n ) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.

Иногда такие сочетания называют сочетаниями без повторений.

Число всевозможных сочетаний из из n элементов по m элементов обозначают

Формула для подсчёта числа сочетаний:

Используя данную формулу можно отметить основные свойства сочетаний.

Простейшие свойства сочетаний:

Доказательства свойства сочетаний

При возведении суммы или разности двух чисел во вторую или третью степень мы пользовались формулами сокращенного умножения, которые являются частным случаем бинома Ньютона.

Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.

Числа являются коэффициентами в формуле бинома Ньютона:

Для более простого подсчета коэффициентов Бинома Ньютона для невысоких степеней удобно пользоваться треугольником Паскаля:

По бокам в каждой строчки имеется коэффициент, равный единице. Все средние коэффициенты считаются, как сумма верхних, которые находятся над ними.

Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.

Не трудно заметить, что строки треугольника симметричны относительно вертикальной оси. Это еще одно замечательное свойство треугольника Паскаля

Историческая справка

Исаак Ньютон (1642-1727 гг.) – выдающийся английский ученый, один из создателей классической физики. Биография Ньютона богата во всех смыслах этого слова. Он сделал немало открытий в области физики, астрономии, механике и математике. Ньютон является автором фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета, заложил основы современной физической оптики, создал многие другие математические и физические теории.

А при чем же здесь бином Ньютона и биномиальные коэффициенты? Формула

была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени произвольное рациональное число (возможно, отрицательное).

Примеры и разбор решения заданий тренировочного модуля

В вазе лежат двенадцать конфет, четыре из которых шоколадные, а остальные карамель. Вы хотите угоститься, выбрав две шоколадные и три карамельные конфеты. Сколькими способами вы можете это сделать?

Мы имеем два события. Это выбор шоколадных и выбор карамельных конфет. Порядок конфет не важен. Поэтому мы можем использовать формулу сочетания для каждого из событий. Так, как шоколадных конфет всего четыре, а выбрать мы хотим две, то это можно сделать способами .

Теперь посчитаем количество выбора карамельных конфет. Их общее количество в вазе 12-4=8, а выбрать мы хотим три. Рассчитаем сочетание из восьми по три.

События выбора разных видов конфет между собой независимы, поэтому по правилу умножения получаем

Представить разложение двучлена в n степени в виде многочлена, где n=0, 1, 2, …,5

Первые четыре разложения мы хорошо умеем делать, используя формулы квадрата и куба разности.

А для представления бинома четвертой и пятой степени воспользуемся треугольником Паскаля.

Наука собственными силами

Сочетания

Свойства сочетаний

Числа C k n обладают целым рядом замечательных свойств. Эти свойства можно доказать по-разному. Можно доказывать алгебраически – прямо воспользоваться формулой (8)

Но можно эти же свойства доказывать и чисто комбинаторными соображениями.

Свойствo 1

В формулу для C k n верхним индексом подставим (n-k). Получим

Однако намного изящнее комбинаторное доказательство:

Что значит «выбрать n-k предметов из n»? Это все равно что «указать k предметов, которые не будут выбраны». Т.е. выбрать n-k предметов из n можно столькими же способами, что и k предметов.

Этим свойством удобно пользоваться, когда верхний индекс ненамного меньше нижнего. Сравните, к примеру, два способа вычисления C 5 7:

напрямую используя формулу (8):

или применяя формулу (9):
Не правда ли, второй проще?

Свойство 2

Запишем правую часть, используя формулу (8) для числа сочетаний:

Приведем к общему знаменателю, равному n!∙(n-k)!:

Однако и здесь комбинаторное доказательство намного красивее:

Все сочетания из n по k (их количество равно C k n ) можно разбить на два класса: содержащие элемент под номером n и не содержащие его.

Выбрать из n элементов k штук, включая n-й – это все равно, что из оставшихся n-1 элементов выбрать k-1. Это можно сделать C k-1 n-1 способами.

Если же n-й элемент в сочетание не входит, то все k элементов нужно выбирать из оставшихся n-1 элементов. Это можно сделать C k n-1 способами.

Так как каждое сочетание из n по k входит или в один, или в другой класс, но не в оба сразу, можно применить правило суммы, и получить доказываемое равенство:

(10).

Свойство 3

В левой части равенства стоит количество всех сочетаний из n элементов (независимо от числа элементов в самих сочетаниях).

О каждом элементе мы можем принять решение: брать его в сочетание или не брать. Т.е. для каждого элемента есть два варианта решения: «да» и «нет». Будем для обозначения того или иного сочетания класть на каждый элемент монетку, причем «да» будем обозначать орлом, а «нет» – решкой. Таким образом, каждому сочетанию из n элементов будет соответствовать ряд из n монет. В разделе «Основные законы комбинаторики» мы доказали, что для n монет возможны 2n вариантов распределения орлов и решек. Поэтому количество всех сочетаний из n элементов равно 2n, что и требовалось доказать.
Перейти к следующей главе →

Комбинаторика: размещения и сочетания

При решении задач по комбинаторике используют следующие важные понятия

Факториалы

Перестановки

Размещения

Сочетания

Размещения

Рассмотрим следующую задачу.

Задача . 9 карточек пронумерованы числами 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

Решение .Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

На первое место можно положить одну из 9 карточек. Для этого есть 9 способов. В каждом из этих 9 способов на второе место можно положить одну из оставшихся 8 карточек. Таким образом, существует

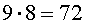
способа, чтобы положить карточки на первое и второе места. В каждом из этих 72 способов на третье место можно положить одну из оставшихся 7 карточек. Следовательно, существует

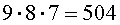
способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих 504 способов на четвертое место можно положить одну из оставшихся 6 карточек. Отсюда вытекает, что существует

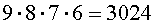
различных способа, чтобы выложить в ряд 4 карточки из набора, состоящего из 9 пронумерованных карточек. Таким образом, при выкладывании карточек можно получить 3024 различных четырехзначных числа.

Ответ : 3024 .

При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

Определение 1 . Рассмотрим множество, содержащее n элементов, и все его упорядоченные подмножества, содержащие k элементов. Каждое из этих подмножеств называют размещением из n элементов по k элементов.

Если обозначить символом 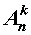число размещений из n элементов по k элементов , то будет справедлива формула:

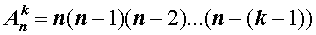
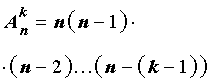
В соответствии с определением факториала, формулу (1) можно также записать в виде:

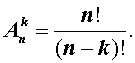
В задаче множеством из n элементов является исходный набор из 9 пронумерованных карточек, а упорядоченным подмножеством из k элементов – 4 карточки, выложенные в ряд.

Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из 9 элементов по 4 элемента, т.е. число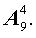

В соответствии с формулой (1),

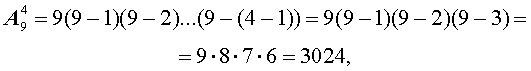
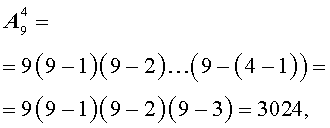
что и было получено в задаче.

Замечание 1 . Введенные в данном разделе размещения также называют размещениями без повторений .

Замечание 2 . Из формул для числа перестановок и числа размещений вытекает формула

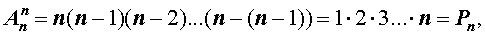
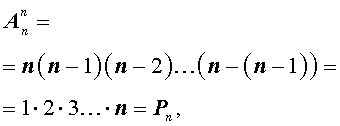
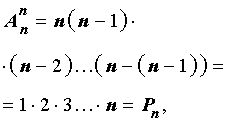
смысл которой заключается в следующем.

Утверждение . Размещение из n элементов по n элементов является перестановкой из n элементов.

Сочетания

Определение 2 . Рассмотрим множество, состоящее из n элементов. Каждое его подмножество, содержащее k элементов, называют сочетанием из n элементов по k элементов .

Число сочетаний из n элементов по k элементов обозначается символом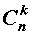

Замечание 3 . Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие k элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем k элементов (из определения 2), совершить всевозможные перестановки, количество которых равно k ! , то мы получим все размещения.

Таким образом, справедлива формула:

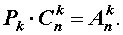
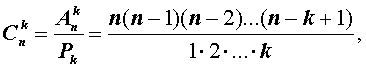
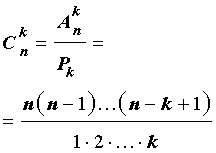
откуда вытекает формула

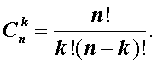(2)

Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):

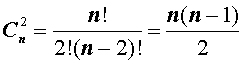
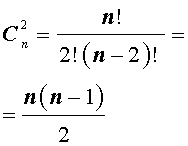
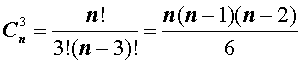
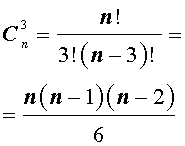
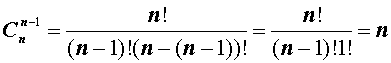
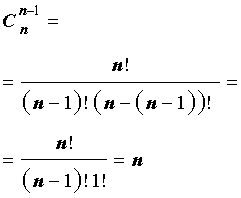
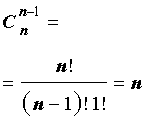
В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):

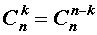
Замечание 4 . С разделом справочника «Сочетания» близко связан раздел «Бином Ньютона», где приведены и доказаны свойства чисел сочетаний.

С понятиями факториала числа n и перестановок из n элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.

Число сочетаний – свойства, формулы и примеры решения

тБУУНПФТЙН УМЕДХАЭЙЕ ЧПЪНПЦОЩЕ УРПУПВЩ ЧЩВПТБ.

1. чЩВПТ У ЧПЪЧТБЭЕОЙЕН: ЛБЦДЩК ЧЩОХФЩК ЫБТ ЧПЪЧТБЭБЕФУС Ч ХТОХ, ЛБЦДЩК УМЕДХАЭЙК ЫБТ ЧЩВЙТБЕФУС ЙЪ РПМОПК ХТОЩ. ч РПМХЮЕООПН ОБВПТЕ ЙЪ ОПНЕТПЧ ЫБТПЧ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ. 2. чЩВПТ ВЕЪ ЧПЪЧТБЭЕОЙС: ЧЩОХФЩЕ ЫБТЩ Ч ХТОХ ОЕ ЧПЪЧТБЭБАФУС, Й Ч РПМХЮЕООПН ОБВПТЕ ОЕ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ.

хУМПЧЙНУС, ЛБЛЙЕ ТЕЪХМШФБФЩ ЧЩВПТБ (ОБВПТЩ ЙЪ ОПНЕТПЧ ЫБТПЧ) НЩ ВХДЕН УЮЙФБФШ ТБЪМЙЮОЩНЙ. еУФШ ТПЧОП ДЧЕ ЧПЪНПЦОПУФЙ.

1. чЩВПТ У ХЮЈФПН РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН ЙМЙ РПТСДЛПН ОПНЕТПЧ. фБЛ, РТЙ ЧЩВПТЕ ФТЈИ ЫБТПЧ ЙЪ ХТОЩ, УПДЕТЦБЭЕК 5 ЫБТПЧ, ОБВПТЩ (1, 5, 2), (2, 5, 1) Й (4, 4, 5) ТБЪМЙЮОЩ, ЕУМЙ РПТСДПЛ ХЮЙФЩЧБЕФУС. 2. чЩВПТ ВЕЪ ХЮЈФБ РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН. оБВПТЩ, ПФМЙЮБАЭЙЕУС МЙЫШ РПТСДЛПН УМЕДПЧБОЙС ОПНЕТПЧ, УЮЙФБАФУС ПДЙОБЛПЧЩНЙ.

фБЛ, ОБВПТЩ (1, 5, 2) Й (2, 5, 1) ОЕ ТБЪМЙЮБАФУС Й ПВТБЪХАФ ПДЙО Й ФПФ ЦЕ ТЕЪХМШФБФ ЧЩВПТБ, ЕУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБЕФУС.

рПДУЮЙФБЕН, УЛПМШЛП ЧПЪНПЦОП ТБЪМЙЮОЩИ ТЕЪХМШФБФПЧ ДМС ЛБЦДПК ЙЪ ЮЕФЩТЈИ УИЕН ЧЩВПТБ (ЧЩВПТ У ЧПЪЧТБЭЕОЙЕН ЙМЙ ВЕЪ, Й Ч ЛБЦДПН ЙЪ ЬФЙИ УМХЮБЕЧ У ХЮЈФПН РПТСДЛБ ЙМЙ ВЕЪ).

Й ОБЪЩЧБЕФУС ЮЙУМПН ТБЪНЕЭЕОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.

ТБЧОП . дМС ЛБЦДПК ФБЛПК РБТЩ ЕУФШ УРПУПВБ ЧЩВТБФШ ФТЕФЙК ЫБТ. рП ФЕПТЕНЕ 1, ЮЙУМП ЧПЪНПЦОЩИ ФТПЕЛ

ТБЧОП РТПЙЪЧЕДЕОЙА ЮЙУМБ РБТ Й ЮЙУМБ УРПУПВПЧ ЧЩВПТБ ФТЕФШЕЗП ЫБТБ, Ф.Е. ТБЧОП . рТПДПМЦБС ТБУУХЦДЕОЙС, РПМХЮЙН, ЮФП ПВЭЕЕ ЮЙУМП ЧПЪНПЦОЩИ ОБВПТПЧ ЙЪ ЫБТПЧ ТБЧОП . ч ЬФПН РТПЙЪЧЕДЕОЙЙ УПНОПЦЙФЕМЕК РПУМЕДОЙК НОПЦЙФЕМШ ЕУФШ ЮЙУМП УРПУПВПЧ ЧЩВПТБ -ЗП ЫБТБ, ЛПЗДБ ХЦЕ ЧЩВТБОЩ РТЕДЩДХЭЙЕ.

Й ОБЪЩЧБЕФУС ЮЙУМПН УПЮЕФБОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.

У ХЮЈФПН РПТСДЛБ	ВЕЪ ХЮЈФБ РПТСДЛБ
(1,1)	(1,1)
(2,2)	(2,2)
(1,2) (2,1)	> (1,2)

чЙДЙН, ЮФП Ч УИЕНЕ «ВЕЪ ХЮЈФБ РПТСДЛБ» РПМХЮЙМПУШ ФТЙ ТБЪМЙЮОЩИ ТЕЪХМШФБФБ, Ч ПФМЙЮЙЕ ПФ ЮЕФЩТЈИ ТЕЪХМШФБФПЧ Ч УИЕНЕ «У ХЮЈФПН РПТСДЛБ». ъБНЕФЙН ФБЛЦЕ, ЮФП ОЙЛБЛЙН ДЕМЕОЙЕН ОБ «ЮЙУМП ЛБЛЙИ-ОЙВХДШ РЕТЕУФБОПЧПЛ», ЛПФПТПЕ РПНПЗМП ЙЪВБЧЙФШУС ПФ ХЮЈФБ РПТСДЛБ РТЙ ЧЩВПТЕ ВЕЪ ЧПЪЧТБЭЕОЙС, ЮЙУМП 3 ЙЪ ЮЙУМБ 4 РПМХЮЙФШ ОЕ ХДБУФУС.

рТЕДУФБЧЙН УЕВЕ ДТХЗПК ЬЛУРЕТЙНЕОФ, ЙНЕАЭЙК ФПЮОП ФБЛЙЕ ЦЕ ТЕЪХМШФБФЩ, Й РПУЮЙФБЕН ЙИ ЛПМЙЮЕУФЧП. еУФШ СЭЙЛПЧ, Ч ЛПФПТЩИ ТБЪНЕЭБАФУС ЫБТПЧ. оБУ ЙОФЕТЕУХЕФ ФПМШЛП ЮЙУМП ЫБТПЧ Ч ЛБЦДПН СЭЙЛЕ. тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ УОПЧБ СЧМСЕФУС ОБВПТ ЮЙУЕМ , ЗДЕ ТБЧОП ЮЙУМХ ЫБТПЧ Ч СЭЙЛЕ У ОПНЕТПН , Й . юЙУМБ РТЙОЙНБАФ ОБФХТБМШОЩЕ ЪОБЮЕОЙС ЙМЙ ТБЧОЩ ОХМА.

б ФЕРЕТШ ЙЪПВТБЪЙН ТЕЪХМШФБФ ФБЛПЗП ТБЪНЕЭЕОЙС Ч ЧЙДЕ УИЕНЩ, Ч ЛПФПТПК ЧЕТФЙЛБМШОЩЕ МЙОЙЙ ПВПЪОБЮБАФ РЕТЕЗПТПДЛЙ НЕЦДХ СЭЙЛБНЙ, Б ФПЮЛЙ ОБИПДСЭЙЕУС Ч СЭЙЛБИ ЫБТЩ:

нЩ ЧЙДЙН ТЕЪХМШФБФ ТБЪНЕЭЕОЙС ДЕЧСФЙ ЫБТПЧ РП УЕНЙ СЭЙЛБН. рЕТЧЩК СЭЙЛ УПДЕТЦЙФ ФТЙ ЫБТБ, ЧФПТПК Й ЫЕУФПК СЭЙЛЙ РХУФЩ, ФТЕФЙК СЭЙЛ УПДЕТЦЙФ ПДЙО ЫБТ, Ч ЮЕФЧЈТФПН Й РСФПН СЭЙЛБИ МЕЦЙФ РП ДЧБ ЫБТБ. рЕТЕМПЦЙН ПДЙО ЫБТ ЙЪ РЕТЧПЗП СЭЙЛБ ЧП ЧФПТПК Й ЙЪПВТБЪЙН ФБЛЙН ЦЕ ПВТБЪПН ЕЭЈ ДЧБ ТЕЪХМШФБФБ ТБЪНЕЭЕОЙС:

чЙДЙН, ЮФП ЧУЕ ТБЪНЕЭЕОЙС НПЦОП РПМХЮЙФШ, НЕОСС НЕЦДХ УПВПК ЫБТЩ Й РЕТЕЗПТПДЛЙ, ЙМЙ ТБУУФБЧМСС ЫБТПЧ ОБ НЕУФБИ. юЙУМП РПМХЮБЕФУС ФБЛ: Х СЭЙЛПЧ ЕУФШ ТПЧОП РЕТЕЗПТПДЛБ, УЮЙФБС ЛТБКОЙЕ, ОП ЙЪ ОЙИ РЕТЕНЕЭБФШ НПЦОП МЙЫШ ЧОХФТЕООАА РЕТЕЗПТПДЛХ. фБЛЙН ПВТБЪПН, ЙНЕЕФУС НЕУФ, ЛПФПТЩЕ НПЦОП ЪБОСФШ ЫБТБНЙ МЙВП ЧОХФТЕООЙНЙ РЕТЕЗПТПДЛБНЙ. рЕТЕВТБЧ ЧУЕ ЧПЪНПЦОЩЕ УРПУПВЩ ТБУУФБЧЙФШ ЫБТПЧ ОБ ЬФЙИ НЕУФБИ (ЪБРПМОСС ПУФБЧЫЙЕУС НЕУФБ РЕТЕЗПТПДЛБНЙ), РЕТЕВЕТЕН ЧУЕ ОХЦОЩЕ ТБЪНЕЭЕОЙС.

пУФБМПУШ ЪБНЕФЙФШ, ЮФП УРПУПВПЧ ТБУУФБЧЙФШ ЫБТПЧ ОБ НЕУФБИ УХЭЕУФЧХЕФ

йНЕООП УФПМШЛП ЕУФШ УРПУПВПЧ ЧЩВТБФШ ЙЪ ОПНЕТПЧ НЕУФ ОПНЕТПЧ НЕУФ ДМС ЫБТПЧ.

Комбинаторика: основные правила и формулы.

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k