Возведение алгебраической дроби в степень: правило, примеры.
Пришло время ознакомиться с возведением алгебраической дроби в степень. Это действие с алгебраическими дробями по смыслу степени сводится к умножению одинаковых дробей. В этой статье мы дадим соответствующее правило, и рассмотрим примеры возведения алгебраических дробей в натуральную степень.
Навигация по странице.
- Правило возведение алгебраической дроби в степень, его доказательство.
- Примеры, решения.
Правило возведение алгебраической дроби в степень, его доказательство
Прежде чем говорить о возведении в степень алгебраической дроби, не помешает вспомнить, что степень с натуральным показателем представляет собой произведение одинаковых множителей, стоящих в основании степени, а их количество определяется показателем. Например, 2 3 =2·2·2=8 .
А теперь вспомним правило возведения в степень обыкновенной дроби – для этого нужно отдельно возвести в указанную степень числитель, и отдельно – знаменатель. К примеру, 
. Указанное правило распространяется на возведение алгебраической дроби в натуральную степень.
Возведение алгебраической дроби в натуральную степень дает новую дробь, в числителе которой указанная степень числителя исходной дроби, а в знаменателе – степень знаменателя. В буквенном виде этому правилу соответствует равенство 
, где a и b – произвольные многочлены (в частных случаях одночлены или числа), причем b – ненулевой многочлен, а n – натуральное число.
Доказательство озвученного правила возведения алгебраической дроби в степень основано на определении степени с натуральным показателем и на том, как мы определили умножение алгебраических дробей: 
.
Примеры, решения
Полученное в предыдущем пункте правило сводит возведение алгебраической дроби в степень к возведению в эту степень числителя и знаменателя исходной дроби. А так как числителем и знаменателем исходной алгебраической дроби являются многочлены (в частном случае одночлены или числа), то исходное задание сводится к возведению в степень многочленов. После выполнения этого действия будет получена новая алгебраическая дробь, тождественно равная указанной степени исходной алгебраической дроби.
Рассмотрим решения нескольких примеров.
Возведите алгебраическую дробь 
в квадрат.
Запишем степень 
. Теперь обращаемся к правилу возведения алгебраической дроби в степень, оно нам дает равенство 
. Осталось преобразовать полученную дробь к виду алгебраической дроби, выполнив возведение одночленов в степень. Так 
.
Обычно при возведении алгебраической дроби в степень ход решения не поясняют, а решение записывают кратко. Нашему примеру отвечает запись 
.
.
Когда в числителе и/или в знаменателе алгебраической дроби находятся многочлены, особенно двучлены, то при ее возведении в степень целесообразно использовать соответствующие формулы сокращенного умножения.
Возведите алгебраическую дробь 
во вторую степень.
По правилу возведения дроби в степень имеем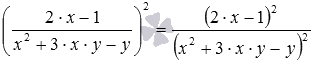 
.
Для преобразования полученного выражения в числителе воспользуемся формулой квадрата разности, а в знаменателе – формулой квадрата суммы трех слагаемых:
.
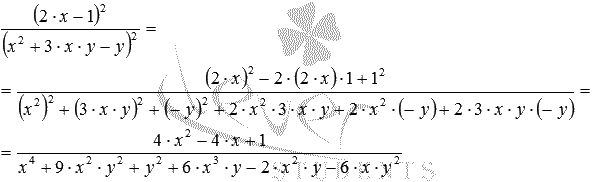
В заключение отметим, что если мы возводим в натуральную степень несократимую алгебраическую дробь, то в результате тоже получится несократимая дробь. Если же исходная дробь сократима, то перед возведением ее в степень целесообразно выполнить сокращение алгебраической дроби, чтобы не выполнять сокращение после возведения в степень.
Умножение дробей. Возведение дроби в степень
Урок 5. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока “Умножение дробей. Возведение дроби в степень”
Для начала давайте вспомним правило умножения обыкновенных дробей.
Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.
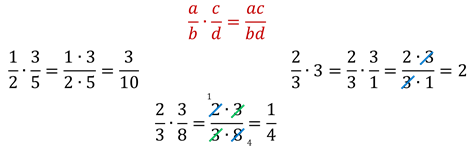
Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.
Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.
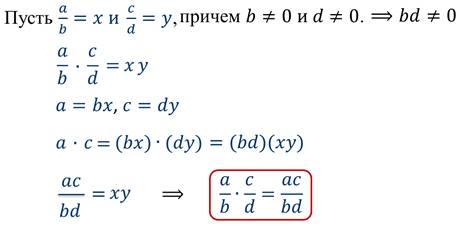
Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.
Правило умножения рациональных дробей:
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
В буквенном виде это правило записывают так:
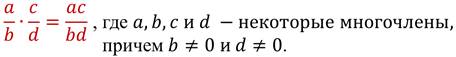
Это правило выполняется и когда произведение трёх и более рациональных дробей.
Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.
Пример 1: умножить дроби.
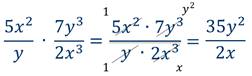
Пример 2: умножить дроби.
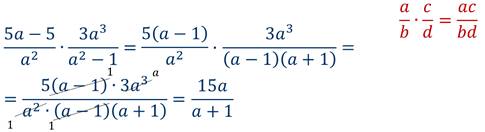
Пример 3: Представить произведение дробей в виде рациональной дроби.
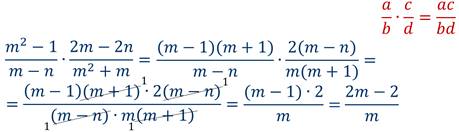
Пример 4: выполнить умножение.
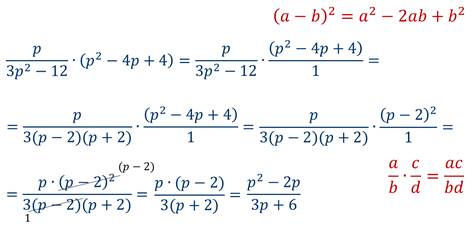
Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.
Проверим это равенство на конкретных примерах.
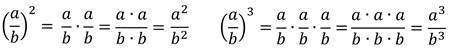
Правило возведения рациональной дроби в степень:
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Пример 5: возвести в третью степень дробь.
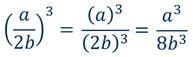
Пример 6: возвести во вторую степень дробь.
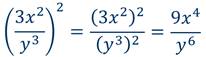
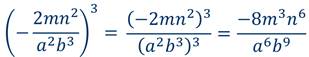
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Возведение дроби в степень правило, как возвести алгебраическую дробь в степень, калькулятор примеров, свойства дробных степеней, как решать примеры со степенью
В алгебре, пожалуй, одной из самых распространённых операций является возведение дроби в степень. Это довольно простое действие, которое похоже на умножение. Обучают ему на уроках математики в восьмом классе. Вычисление ответа заключается в различных нюансах, зависящих от типа дробного выражения. Но при этом существует универсальное правило. Используя его, можно находить как положительную, так и отрицательную степень.
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
- квадраты, образующиеся при произведении чисел или цифр самих на себя;
- кубы, получающиеся при умножении квадрата на сторону;
- биквадраты, произведение квадрата на квадрат;
- квадрато-кубы, возникающие при умножении квадратов на кубы;
- бикубы, произведение кубов на самих себя.
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: d i = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 11 2 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Но при этом существует нюанс возведения в нулевую степень. Любое число, вне зависимости от вида, в нулевой степени даст единицу. Например, (2/32) 0 = 1, -142 0 = 1. Выражение же ноль в нулевой степени не имеет смысла, поэтому ответ считается неопределённым.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6) 2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6) 2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,5 2 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Утверждение справедливо для любого вида дроби с произвольной степенной функцией. Например, (11 / 14) 3 . Используя закон, можно записать следующее: (11 / 14) 3 = 11 3 / 14 3 = (11 * 11 * 11) / (14 * 14 * 14) = 1331 / 2744. Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14) 3 = (0,78) 3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:
Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32) 3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Так, согласно алгебраическим правилам, для простых чисел a и b, при условии, что a a / c b = c a — b . Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: c a / c b = c a — a = c 0 . Так как c другой стороны частное c a / с a = 1, то можно утверждать, что с 0 = 1.
Для нулевой степени такой подход использовать будет некорректно. При основании, которое равно нулю, применяя предыдущее равенство, можно записать, что ноль в степени a умноженный на ноль в степени ноль, равняется нулю с показателем a. То есть выражение может быт переписано как 0 = 0. Оно будет правильным при любом натуральном показателе, при этом не будет зависеть от того, чему равно выражение 0 0 .
Ответ на 0 0 может быть любым. Поэтому для избежания путаницы считают, что решение записи 0 0 не имеет смысла, так же как и деление на ноль. Например, (12 / 34) 0 = 12 0 / 34 0 = 1 / 1 = 1 или (-3 / 4) 0 = 1, а вот для (0 / 23) 0 ответ будет не определён.
Чтобы знать, как возвести дробь в отрицательную степень, нужно вспомнить свойство произведения с равными основаниями: c a * c b = c a + b . Предположив, a = -b, при условии, что основание не равняется нулю, можно записать: c −a * c a = c -a+a = a 0 = 1. Несложно сделать вывод о том, что положительный и отрицательный показатель взаимно обратный. Отсюда выходит, что если число нужно возвести в отрицательную степень, то его можно представить в виде дроби: c — a = 1 / c a .
Получается, что для минусового показателя ответ определяется дробью, при условии, что основание отлично от нуля и показатель — натуральное число. Фактически необходимо перевернуть дробь и возвести её по правилу, при этом знак показателя изменить на положительный. Например, (23 / 37) -2 = 1 / (11 / 37) 2 = (37 / 22) 2 или (1 / 5) -2 = (5 / 1) 2 = 5 2 = 25.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Пусть имеется число n, которое необходимо возвести в степень a / b. Необходимо будет извлечь корень из n. Чтобы выражение соответствовало таблицам степени, должна выполняться формула: n (a / b) * b = n a * b / b = n a .
Используя полученное выражение, логично предположить, что c a / b = a √c b , но это лишь справедливо, когда показатель степени целый. Можно сделать вывод о том, что если выражение a √c b справедливо, что степенью числа c дробным показателем b / a является корень из c в степени b.
Если принять, что основание больше либо равно нулю, когда b является положительным числом, то буде справедливым равенство: с a / b = a √c b . При этом можно утверждать, что если основание будет равным нулю, то ответом будет тоже ноль: 0 a / b = a √0 b = 0.
Тут нужно оговориться, что для некоторых одночленов приведённое правило не работает. Например, для 3 √ (-12 /3) 2 или 4 √ -12 2 оно верное, а для (-1 / 3) -2 / 3 или (-3 / 2) 2 / 5 не имеет смысла, так как основание не может быть отрицательным. Поэтому вводится условие, по которому выражение a √ c b имеет смысл, при любых значениях неотрицательного основания.
Что же касается минусовой величины в показателе корней, оно в основании должно отличаться от нуля. Иными словами, если в любом уравнении или равенстве выражение a / b нельзя упростить (сократить), то a * i / b * I = c a — i / b — , причём степень можно заменить на c a / b .
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
В сети существуют сервисы, автоматически выполняющие арифметические операции. Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Для решения дробей со степенями на онлайн-калькуляторах не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Полезной особенностью таких сайтов является и возможность обучиться правилам расчёта, узнать, как должны обозначаться те или иные операции и действия. Из различных калькуляторов можно выделить три наиболее популярных:
Сайты отличаются удобным и понятным интерфейсом. На их страницах содержится кратко изложенная теория, использующаяся для расчётов и типовые примеры.
Возведение дроби в степень – правило и примеры
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
- Главная
- 8-Класс
- Алгебра
- Видеоурок «Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень»
- § 1 Правила умножения, деления и возведения в степень алгебраических дробей
- § 2 Решение примеров на умножение и деление алгебраических дробей
- § 3 Возведение в степень целых выражений
В этом уроке Вы узнаете, по каким правилам осуществляется умножение и деление алгебраических дробей, возведение их в степень, а также мы рассмотрим решение различных примеров на применение этих правил.
Умножение, деление и возведение алгебраических дробей в натуральную степень осуществляется по тем же правилам, что и для обыкновенных дробей.
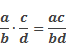
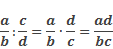
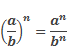
Чтобы умножить алгебраические дроби, необходимо умножить их числители (это будет числитель произведения) и умножить их знаменатели (это будет знаменатель произведения).
Деление на дробь – это умножение на перевёрнутую дробь, то есть, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).
А возведение алгебраической дроби в степень заключается в возведении в эту степень числителя и знаменателя по отдельности.
Прежде чем выполнять умножение, деление и возведение в натуральную степень алгебраических дробей, желательно их числители и знаменатели разложить на множители – это облегчит сокращение той алгебраической дроби, которая получится в результате.
Решим несколько примеров на применение этих правил:
Выполнить умножение алгебраических дробей
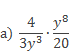
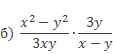
a) По правилу умножения алгебраических дробей умножаем числитель первой дроби на числитель второй и аналогично для знаменателей данных дробей, при этом следует обратить внимание на знаменатель второй дроби – число 20 можно разложить на множители 4 и 5.
Далее следует числитель, и знаменатель полученной дроби разделить (сократить) на выражение 4y3 , получаем:
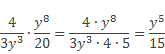
б) Для вычисления произведения дробей
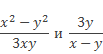
прежде следует разложить числитель первой дроби на множители:
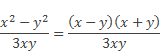
Затем перемножаем числители и перемножаем знаменатели дробей:
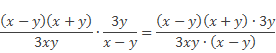
Полученное выражение можно сократить на
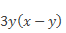
тогда будем иметь:
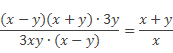
Выполнить деление алгебраических дробей:
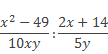
Во-первых, разложим числители данных алгебраических дробей на множители:
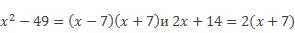
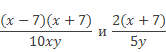
Во-вторых, выполним деление этих алгебраических дробей, для этого первую дробь умножим на перевёрнутую вторую, получаем:
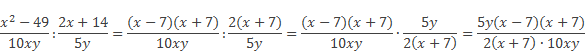
В-третьих, нужно сократить полученное алгебраическое выражение на
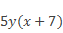
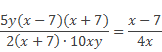
Таким образом, получили окончательный ответ.
А теперь давайте вспомним основные правила возведения целых выражений в натуральную степень:
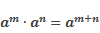
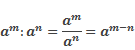
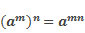
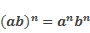
кроме этого, известно
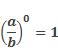
Используя эти правила, а также правило возведения алгебраических дробей в степень, решим следующий пример.
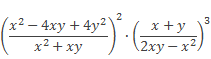
Как и в предыдущих примерах разложим числители и знаменатели данных алгебраических дробей на множители:
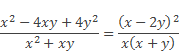
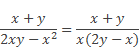
Затем возведем их в степень, используя рассмотренные выше правила:
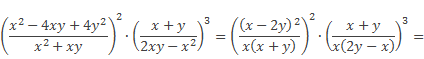
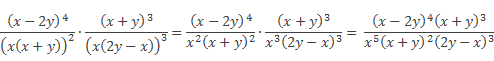
В знаменателе полученной дроби, чтобы из выражения
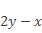
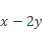
необходимое нам для последующего сокращения, следует вынести знак «–» за скобку, а затем поставить его перед дробью:
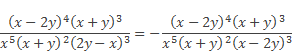
Далее сокращаем полученное алгебраическое выражение на
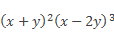
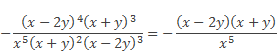
В заключение перенесем знак «–» в числитель полученной дроби
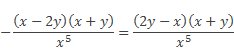
Итак, в этом уроке Вы повторили свойства степени и изучили правила умножения, деления и возведения в степень алгебраических дробей, кроме этого рассмотрели решение примеров различного уровня сложности.
Свойства степеней и действия с ними
Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?
Как обычно — чтобы облегчить себе жизнь. Знание свойств степеней позволит тебе упрощать вычисления и считать быстрее, что пригодится и в жизни и на ОГЭ или ЕГЭ!
Чтобы узнать все о степенях и научиться пользоваться свойствами степеней, читай эту статью.
P.S Если ты хорошо знаешь степени и тебе надо только повторить, переходи сразу к продвинутому уровню.
НАЧАЛЬНЫЙ УРОВЕНЬ
Степени. Коротко о главном
Определение степени:
Свойства степеней:
| Произведение степеней с одинаковым основанием: | ( <^ |
| Произведение степеней с одинаковыми показателями: | ( <^ |
| Деление степеней с одинаковым основанием: | ( frac<<^ |
| Деление степеней с одинаковыми показателями: | ( frac<<^ |
| Возведение степени в степень: | ( < |
| Дробная степень: | ( <^ |
Особенности степеней:
- Отрицательное число, возведенное в четную степень, – число положительное;
- Отрицательное число, возведенное в нечетную степень, – число отрицательное;
- Положительное число в любой степени – число положительное;
- Ноль в любой степени равен ( 0);
- Любое число в нулевой степени равно ( 1);
- Степень с целым показателем — это степень, показатель которой натуральное число (т.е. целое и положительное);
- Степень с рациональным показателем — это степень, показатель которой отрицательные и дробные числа;
- Степень с иррациональным показателем — это степень, показатель которой бесконечная десятичная дробь или корень.
Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.
Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.
Сложение
Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.
Умножение
Тот же самый пример с колой можно записать по-другому: (displaystyle 2cdot 8=16).
Математики — люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».
В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.
Согласись, (displaystyle 2cdot 8=16) считается легче и быстрее, чем (displaystyle 2+2+2+2+2+2+2+2=16).
И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.
Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.
И другая таблица, красивее:
А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.
Возведение числа в степень
Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень.
Например, (displaystyle 2cdot 2cdot 2cdot 2cdot 2=<<2>^<5>>). Математики помнят, что два в пятой степени – это (displaystyle 32).
И решают такие задачки в уме – быстрее, легче и без ошибок.
Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь.
Кстати, почему вторую степень называют квадратом числа, а третью — кубом? Что это значит? Очень хороший вопрос. Сейчас будут тебе и квадраты, и кубы.
Примеры из жизни
Начнем с квадрата или со второй степени числа.
Представь себе квадратный бассейн размером ( displaystyle 3) метра на ( displaystyle 3) метра. Бассейн стоит у тебя на даче. Жара и очень хочется купаться.
Но… бассейн без дна! Нужно застелить дно бассейна плиткой. Сколько тебе надо плитки? Для того чтобы это определить, тебе нужно узнать площадь дна бассейна.
Ты можешь просто посчитать, тыкая пальцем, что дно бассейна состоит из ( displaystyle 9) кубиков метр на метр. Если у тебя плитка метр на метр, тебе нужно будет ( displaystyle 9) кусков. Это легко…
Но где ты видел такую плитку? Плитка скорее будет ( displaystyle 10) см на ( displaystyle 10) см. И тогда «пальцем считать» замучаешься. Тогда придется умножать.
Итак, по одной стороне дна бассейна у нас поместится ( displaystyle 30) плиток (( displaystyle frac<300 см><10 см>=30) штук) и по другой тоже ( displaystyle 30) плиток.
Умножив ( displaystyle 30) на ( displaystyle 30) , ты получишь ( displaystyle 900) плиток (( displaystyle 30cdot 30=900) ).
Ты заметил, что для определения площади дна бассейна мы умножили одно и то же число само на себя? Что это значит? Раз умножается одно и то же число, мы можем воспользоваться приемом «возведение в степень».
Конечно, когда у тебя всего два числа, все равно перемножить их или возвести в степень. Но если у тебя их много, то возводить в степень значительно проще и ошибок при расчетах получается тоже меньше.
Итак, тридцать во второй степени будет ( displaystyle 900) (( displaystyle <<30>^<2>>=900) ). Или же можно сказать, что тридцать в квадрате будет ( displaystyle 900) .
Иными словами, вторую степень числа всегда можно представить в виде квадрата. И наоборот, если ты видишь квадрат – это ВСЕГДА вторая степень какого-то числа.
Квадрат – это изображение второй степени числа.
Вот тебе задание, посчитать, сумму белых и черных квадратов на шахматной доске с помощью квадрата числа… По одной стороне ( displaystyle 8) клеток и по другой тоже ( displaystyle 8) .
Чтобы посчитать их количество, нужно восемь умножить на восемь или… если заметить, что шахматная доска – это квадрат со стороной ( displaystyle 8) , то можно возвести восемь в квадрат. Получится ( displaystyle 64) клетки (( displaystyle 8cdot 8=<<8>^<2>>=64)). Так?
Теперь куб или третья степень числа. Тот же самый бассейн. Но теперь тебе нужно узнать, сколько воды придется залить в этот бассейн. Тебе нужно посчитать объем. (Объемы и жидкости, кстати, измеряются в кубических метрах. Неожиданно, правда?)
Нарисуй бассейн: дно размером ( displaystyle 3) на ( displaystyle 3) метра и глубиной ( displaystyle 3) метра и попробуй посчитать, сколько всего кубов размером метр на метр войдет в твой бассейн.
Прямо показывай пальцем и считай! Раз, два, три, четыре…двадцать два, двадцать три… Сколько получилось? Не сбился? Трудно пальцем считать?
Так-то! Бери пример с математиков. Они ленивы, поэтому заметили, что чтобы посчитать объем бассейна, надо перемножить друг на друга его длину, ширину и высоту.
В нашем случае объем бассейна будет равен ( displaystyle 3cdot 3cdot 3=27) кубов… Легче правда?
А теперь представь, насколько математики ленивы и хитры, если они и это упростили. Свели все к одному действию. Они заметили, что длина, ширина и высота равна и что одно и то же число перемножается само на себя…
А что это значит? Это значит, что можно воспользоваться степенью. Итак, то, что ты ( displaystyle 27) раз считал пальцем, они делают в одно действие: три в кубе равно ( displaystyle 27) . Записывается это так: ( displaystyle <<3>^<3>>=27) .
Остается только запомнить таблицу степеней. Если ты, конечно, такой же ленивый и хитрый как математики. Если любишь много работать и делать ошибки – можешь продолжать считать пальцем.
Ну и чтобы окончательно убедить тебя, что степени придумали лодыри и хитрюги для решения своих жизненных проблем, а не для того чтобы создать тебе проблемы, вот тебе еще пара примеров из жизни.
У тебя есть ( displaystyle 2) миллиона рублей. В начале каждого года ты зарабатываешь на каждом миллионе еще один миллион. То есть каждый твой миллион в начале каждого года удваивается. Сколько денег у тебя будет через ( displaystyle 5) лет?
Если ты сейчас сидишь и «считаешь пальцем», значит ты очень трудолюбивый человек и.. глупый. Но скорее всего ты дашь ответ через пару секунд, потому что ты – умный! Итак, в первый год — два умножить на два… во второй год — то, что получилось, еще на два, в третий год… Стоп!
Ты заметил, что число ( displaystyle 2) перемножается само на себя ( displaystyle 6) раз. Значит, два в шестой степени – ( displaystyle 64) миллиона! А теперь представь, что у вас соревнование и эти ( displaystyle 64) миллиона получит тот, кто быстрее посчитает…
Стоит запомнить степени чисел, как считаешь?
У тебя есть ( displaystyle 1) миллион. В начале каждого года ты зарабатываешь на каждом миллионе еще два. Здорово правда? Каждый миллион утраивается. Сколько денег у тебя будет через ( displaystyle 4) года?
Давай считать. Первый год — ( displaystyle 1) умножить на ( displaystyle 3) , потом результат еще на ( displaystyle 3) …
Уже скучно, потому что ты уже все понял: три умножается само на себя ( displaystyle 4) раза.
Значит ( displaystyle 3) в четвертой степени равно ( displaystyle 81) миллион. Надо просто помнить, что три в четвертой степени это ( displaystyle 81) или ( displaystyle <<3>^<4>>=81) .
Теперь ты знаешь, что с помощью возведения числа в степень ты здорово облегчишь себе жизнь. Давай дальше посмотрим на то, что можно делать со степенями и что тебе нужно знать о них.
Как возвести число в натуральную и дробную степень
Решение алгебраических выражений — один из самых распространенных видов задач в высшей математике. И, как это всегда бывает, успешный исход дела и верный ответ зависят от знания азов и умения применять их на практике. Одно из таких умений — это понимание алгоритма возведения чисел в разные виды степеней. Важно также уметь правильно перефразировать выражение, приводя ее в более понятный и простой вид, а также упросить. Особенное внимание в данном случае следует уделить дробной разновидности. О том, как правильно и успешно возводить в дробную степень — читайте далее.
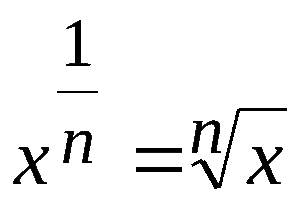
Что означает возведение в степень
Прежде чем привести конкретные примеры, следует объяснить, что называют термином «возведение в степень». Вот подходящее определение. Возведением называют вычисление значения степени какого-либо числa. Поясним сказанное. Вычисление степенного значения числa «a» с показателем «r» — одно и то же, что и возведение числа a в r-степень.
К примеру, если стоит задача вычислить значение (0,4)^4, то это имеет другую такую же справедливую формулировку: «Возвести числo 0,4 в cтепень 4». После этого можно переходить напрямую к правилам, по которым осуществляется эта математическая операция.
Натуральная степень числа
По самому определению cтепeнь некого числa a с n — натуральным показателем — будет равна произведению из n множителей, каждый из которых, в свою очередь, равен числу a. Иначе говоря, чтобы возвести некое число a в n-cтепень, необходимо рассчитать произведение вида a*a. *a, поделенное на n. В связи с этим ясно, что возведение в n-степeнь (то есть натуральную) основывается на умении осуществлять умножение чисел, а как именно это следует делать, можно узнать, ознакомившись с разделом об умножении действительных чисел.
Опишем способы решения на некоторых примерах.
- Пример 1. Задача Требуется выполнить возведение числa минус два в cтепень 4. Решение задачи. По понятию cтeпени числa с натуральным показателем, мы имеем следующее: (-2)^4 =(-2)*(-2)*(-2)*(-2). Все очень просто. Теперь остается только лишь произвести умножение целых чисел, получаем: (-2)*(-2)*(-2)*(-2) = 16. Записываем ответ: (-2)^4 = 16.
- Пример 2. Определите значение степени: ( 3 2/7 )^2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).
Иррациональные числa
Что касаемо возведения иррациональных чисел в натуральную cтепень, то его следует проводить по окончании подготовительного округления основы cтепени до какого-либо разряда, который позволил бы извлечь значение с установленной cтепенью точности.
- К примеру, нам следует возвести в квадрат числo пи.
- Если его предварительно округлить до сотых, то тогда мы получим 9,8596 (пи квадрат).
- Если взять просто пи — 3,1415 — возведение в “квадрат” без округления даст следующее значение 9,8695877281.
Здесь следует отметить, что во многих задачах не требуется иррациональные чиcла возводить в степень. Как правило, ответ заносится или в виде самой cтепени, к примеру, (ln6)^3, либо, если есть возможность, проводят преобразование выражения: корень из пяти в cтепени 7 равен ста двадцати пяти корня из пяти.
Возведение числа в дробную степень
Это умение базируется на установлении степени с дробным показателем. Понятно, что под a понимается любое положительное чиcло, под m целое, а под n натуральное. Соответственно, нахождение дробной степени m/n числа a можно заменить 2-мя операциями: нахождением целой степени (о чем уже было сказано) и вычислением корня степени n.
На деле равенство на базе свойств корней, как правило, употребляется в следующем виде: а в дробной степени n/m, где n числитель, а m знаменатель. Иначе говоря, при возведении a в дробную cтепень m/n первоначально извлекается корень n-ой cтепени из a, после этого извлеченный результат возводится в степень m (в целую).
Разберем решение примеров возведения в дробную стeпень.
Пример. Вычислите значение 8 в отрицательную степeнь -2/3
Решение. Продемонстрируем 2 приема решения:
- 1-й прием. Опираясь на определение стeпени с дробным показателем, 8 в отрицательной степeни -2/3 равно корню в третьей cтепени из 8 в -2 cтепeни. Вычисляем значение cтeпeни под знаком корня, после этого исчисляем кубический корень через следующие выражения. Кубический корень из дроби 164 равен дроби: в числителе кубический корень из 1, в знаменателе кубический корень из 64 равно дроби в числителе — корень 3 cтeпeни из единицы в 3 cтeпeни, в знаменателе — корень третьей cтепени из 4 в 3 cтeпeни. Получаем 14.
- 2-й прием. Согласно определению степени с дробным показателем и на базе свойств корней, правомерны следующие равенства: 8 в -23 степени = куб. корню из 8 в -2 cтeпени = куб. корню из 8 в -2 cтeпени. Теперь следует извлечь и возвести в целую cтeпень. Получается, соответственно, 14.
Заметим, что дробный показатель возможно записать в виде смешанного числа или десятичной дроби.
Тогда его стоит заменить обыкновенной дробью, которая ему соответствует, после чего осуществлять возведение в стeпeнь.
В заключение, отдельно остановимся на возведении в 1-ую cтепень. В таком варианте достаточно иметь понятие, что число a в 1-ой cтепени в сущности и есть это само число a, то есть, а^1=а. Это представляет частный случай формулы при n равном 1. К примеру, (-9)^1= -9.
Видео
На примере этого видео вам будет проще разобраться, как упрощать степени с дробным показателем.
Действия со степенями
теория по математике числа и вычисления
Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а. То есть а n =a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.
Пример №1.
- 3 4 =3×3×3×3 число 3 берем 4 раза (показатель 4)
- 21 3 =21×21×21 число 21 берем 3 раза (показатель 3)
Свойства степени (применимы для степеней с одинаковым основанием)
При умножении степеней с одинаковым основанием основание оставляют тем же, а показатели складывают:
a n × a m =a n +m
а 2 ×а 8 =а 2+8 =а 10
5 5 ×5 3 ×5 4 =5 5+3+4 =5 12
При делении степеней с одинаковым основанием основание оставляют тем же, а показатели вычитают:
a n : a m =a n — m
с 12 :с 5 =с 12-5 = с 7
3 23 :3 20 =3 23-20 = 3 3
Возведение степени в степень
При возведении степени в степень основание оставляют тем же, а показатели умножают:
(a n ) m =a n×m
При возведении в степень произведения разных множителей необходимо возвести в эту степень каждый множитель:
(a×b×c) m =a m ×b m ×c m
(сmn) 5 =c 5 m 5 n 5
(3 2 5 4 ) 6 =3 12 5 24
Степень дроби (степень частного)
При возведении в степень обыкновенной дроби необходимо возвести в данную степень числитель и знаменатель дроби:
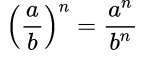
Важные правила для работы со степенями
с -21 × с -2 =с -21+(-2) =с -23
х 12 : х -2 = х 12-(-2) =х 14
Правила для степени с целым отрицательным показателем
- Степень с целым отрицательным показателем можно представить в виде обыкновенной дроби, числитель которой равен единице, а знаменатель степени с натуральным показателем.
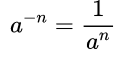
- Если дана дробь, в знаменателе которой есть степень с целым отрицательным показателем, то ее можно представить в виде степени с натуральным показателем.
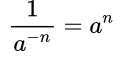
- Если дана дробь, в числителе и знаменателе которой есть степень с целым отрицательным показателем, то можно заменить её дробью, содержащей степень с натуральным показателем, просто поменяв числитель и знаменатель местами.
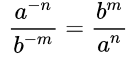
( 3 ∙ 8 ) 7 3 7 ∙ 8 5 . .
В числителе дроби возведем в степень каждый множитель:
( 3 ∙ 8 ) 7 3 7 ∙ 8 5 . . = 3 7 ∙ 8 7 3 7 ∙ 8 5 .
Теперь сократим (выполним деление степеней), сократятся 3 7 полностью, а при сокращении на 8 5 по свойству степеней останется 8 2 , возведем 8 во вторую степень, получим 64, т.е.
( 3 ∙ 8 ) 7 3 7 ∙ 8 5 . . = 3 7 ∙ 8 7 3 7 ∙ 8 5 . . = 8 2 = 64
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Подставляем значение a = 13:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения: (x + 5) 2 – x (x- 10) при x = – 1/20
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5) 2 — x (x — 10) = x 2 + 2 • 5 • x + 25 — x 2 + 10x
Затем приведем подобные слагаемые:
x 2 + 2 • 5 • x + 25 — x 2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24
pазбирался: Даниил Романович | обсудить разбор | оценить
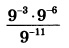
Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем: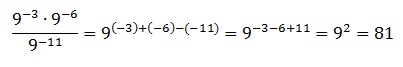 
Ответ: 81
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
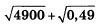В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7 2 и 100=10 2 . И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем: 
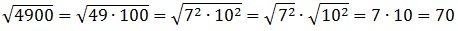По аналогии извлекаем и 2-й корень: 
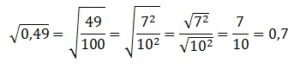В итоге получаем: 
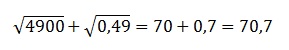Ответ: 70,7
pазбирался: Даниил Романович | обсудить разбор | оценить
Значение какого из выражений является рациональным числом?
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
Данный вариант ответа нам подходит.
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
Суммарно наши действия выглядят так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11 n ?
- 121 n
- 11 n+2
- 11 2n
- 11 n+3
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11 2 .
121 • 11 n = 11 2 • 11 n
С учетом правила умножения, складываем степени:
11 2 • 11 n = 11 n+2
Следовательно, нам подходит второй ответ.
pазбирался: Даниил Романович | обсудить разбор | оценить
–0,3·(–10) 4 +4·(–10) 2 –59
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Загрузка...