Число в нулевой степени

Ноль в степени ноль

Ноль — наверное самое загадочное число и самое контринтуитивное. Ведь его аналога в реальной жизни просто нет. Ноль это отсутствие чего-то. Но почему ноль в степени ноль равняется единице? И главный вопрос, так ли это на самом деле? Можете проверить на своем калькуляторе до того, как прочтете…

Ноль «в степени» ноль

Как такое может быть? А вот как: 1 0 =1, 2 0 =1…. х 0 =1. Любое число при взведении в нулевую степени равняется единице. Чем сам ноль хуже? Но не все так просто.

Что означает возвести в степень? Например «два в квадрате». Что мы делаем, мы двойку умножаем на саму себя 2 раза (2*2=4), «два в кубе», двойку умножаем саму на себя 3 раза (2*2*2=8). А что если степень, это «ноль»? Нужно взять число и умножить само на себя…. ноль раз? Это странно.

Вот как выглядит график функции y=x x

Видно, что при уменьшении значения Х значение У сначала снижается, а потом начинает расти и превращается… в единицу при условии очень маленьких (почти нулевых) значениях Х. Было бы логично предположить, что когда значение уменьшится до ноля, там тоже будет единица.

Еще раз, вернемся к простым цифрам:

Что означает эта запись? Чтобы получить девять, нужно тройку умножить два раза. Правда же?

Сколько раз нужно умножить тройку саму на себя, чтобы получить единицу? А если разделить 1 на 3? Простого ответа нет? Логично, что чем больше значение степени, тем больше результат, и чем меньше это значение, тем и результат меньше.

Но на графике выше показано, что кривая «упирается» в предел, в единицу. Точнее, значение функции становится равным 1, когда ноль еще даже не достигнут. И если уменьшать Х еще больше, все равно, дальше единицы не сдвинутся.

Контекст

Как получается, что при умножении ноля самого на себя получается что-то большее самого ноля?

Если мы в реальной жизни (а не в математике) съели все яблоки и их у нас 0, то сколько бы мы не умножали отсутствующие яблоки на такие же «нулевые» фрукты, как может у нас возникнуть целое яблоко? Если вам кажется такой вопрос простым, так и есть. С одной точки зрения это странное выражение будет равняться единице, а вот с другой оно будет «не определено». То есть никакой единицы а результате умножения ноля на ноль и быть не может, да?

Математика говорит, что:

3 2 ×3 2 это тоже самое, что и 3 2+2 = 3 4 = 3 × 3 × 3 × 3= 81

4 5 ÷4 3 это тоже самое, что и 4 5–3 = 4 2 = 4 × 4 = 16

Тогда, если степени одинаковы:

3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 = Ой?!

Но ведь мы можем и не вычитать степени, а просто сделать две операции отдельно:

3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 , но 3 2 =9, тогда 3 2 ÷3 2 = 3 2-2 или 3 2 ÷3 2 =9÷9=1

А что будет если одно число поделить на самого себя? Единица!

Матанализ

С точки зрения математического анализа, все одновременно и сложно, и совсем просто. Ноль в степени ноль = неопределенность. Что, согласитесь, более логично. Ведь если у нас нет ничего и мы ничего умножим само на себя, не может же возникнуть что-то из этой пустоты?

Теория множеств

Давайте посмотрим с точки зрения теории множеств. Допустим у нас есть два множества.

Первое множество, это количество символов пароля, которым закрыт доступ к вашей страничке в соцсети, или, еще лучше, PIN код банковской карты допустим — 4 символа.

Второе множество, это количество значений, корыте может принимать каждый символ. Предположим, что это только цифры, значит цифр — 10.

Вопрос, сколько вариантов комбинаций существует? Сколько раз нужно ввести случайную комбинацию, чтобы гадать пароль? Каждый символ

10 4 =10 000 тысяч вариантов.

Можно сказать, что множество цифр (10) отображается на множестве возможных символов (4). Но есть и «пустые» множества. Например, вы не поставили пароль вовсе, у вас ноль символов, так сколько попыток понадобится, чтобы получить доступ к счету? Ровно одна.

То есть при 10 0 =1, но тоже самое случится, если пароля нет и значений тоже нет 0 0 =1. Простыми словами, ноль в степени ноль, означает, что пароль не установлен и каждое значение тоже 0. Тогда может существовать только одна такая «комбинация».

А на самом деле?

Практического применения это математическое выражение, как нетрудно догадаться, не имеет вовсе. Ни одном инженеру, ни одному экономисту не придет в голову умножать ноль на ноль ноль раз. Это просто не применимая конструкция. Так что вопрос остается в области математики, и может быть философии.

Это наверное единственный случай, когда оставаясь математиком можно для свободно для себя решать чему равно «0 в степени 0».

“А сколько будет 0 в степени 0?” или прощай мозг.

бескоечно малое число возводим в бесконечно малую степень, получаем еще меньшее число -> ноль
с другой стороны
2^0 = 2^(2-2) = 2^2 : 2^2 = 4 : 4 = 1
0^(2-2)=0^2:0^2=1
это в теории, на практике мы ничто делим на ничто, развергаются небеса, во всем мире происходят извержения вулканов, появляются черные дыры и на землю выползают хедкрабы..

неопределенность, нельзя так делать, как на ноль делить нельзя))

0 можно возводить только в положительную степень, как мне кажется.
Ведь, например, если 0 возводить в степень -1, то получится 1/0, а на 0 делить нельзя. ну а нулевую степень вполне могли приписать к ограничению на неотрицательность)

В общем, либо получится 1 (как любое число в нулевой степени), либо вообще недопустимая операция (как 0 в неположительной степени), но точно не 0))

В программировании существует переменная, хранящая результат.

Допустим, вот псевдокод топорного умножения:

Функция_УМНОЖИТЬ(Множимое M, Множитель N)

ИТОГО = ИТОГО + M

Здесь переменная ИТОГО изначально равна НУЛЮ, так как будет копить Множимое N-раз через сложение.

А вот функцию возведения в степень аналогична, но немного иная:

Функция_ВОЗВЕСТИ(Основание степени M, Показатель степени N)

ИТОГО = ИТОГО * M

Тем самым, переменная ИТОГО изначально не должна равняться НУЛЮ, так как будет копить Основание N-раз через умножение.

Более простым языком: Допустим, имеем уравнение Z=0^Y*X. Если Y равен 1, мы умножаем X на 1 НОЛЬ. Т.е. сокращённая запись принимает вид Z=0*X. Если же Y равен 0, мы не умножаем X ни на что вообще. Т.к. сокращённая запись уже имеет вид Z=X, где нет место НУЛЮ, тем самым, формула включает в себя 0 НОЛЕЙ.

вот почему https://www.youtube.com/watch?v=r0_mi8ngNnM

Любое число в нулевой степени, за исключением нуля, равно единице, гугл.

Сколько будет 0-2=? Если от этой цифры нельзя нечего взять

все визуально просто: постройте график функции, приближаясь все ближе к нулю, сами увидите, что “0” в нулевой степени остановится на точке “1”(плсмотрите ролик Физика Побединского в ютубе “0” в степени “0”)

Думаю примера будет достаточно:

2 ^ 0 = 1 = 1
2 ^ 1 = 1 * 2 = 2
2 ^ 2 = 1 * 2 * 2 = 4
2 ^ 3 = 1 * 2 * 2 * 2 = 8

Мотивации пост

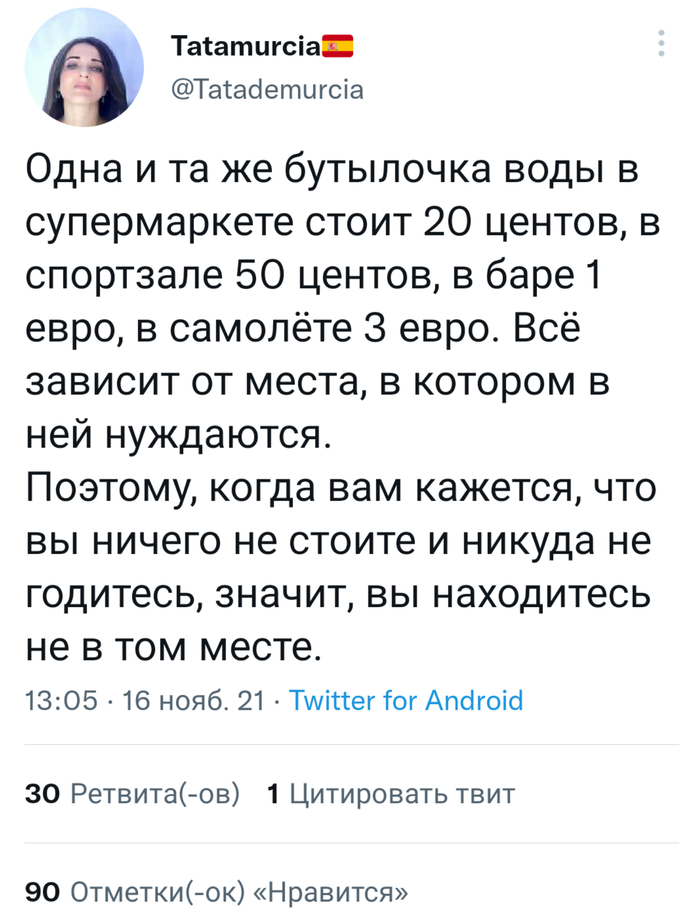
. а в пустыне она вообще бесценна.

Оборот денег в семье.

Старший сын подарил младшей сестре 5000 руб на днюху(13 лет разница).
Сегодня она подходит ко мне:
– Пап, вот 5000 рублей. И вот мои заказы на али. Это подарки тебе, маме, брату, его жене и их мелкому. Успеют же приехать? Можешь оплатить по карте?
– Конечно, доча.
Оплатил. Деньги взял. Ибо это её решение. Добавлю их в её подарок. Но об этом ей, конечно, не скажу.

Новый Год на носу. Подарки. Берегла эти деньги с апреля. Вот так решила их потратить.

У меня хорошие дети.

Не рой яму другому.

Прошу юридической помощи, напали чеченцы в метро

Здравствуйте, я очень сомневался писать пост или нет, но сил уже нет бороться в одиночку с нашей правоохранительной системой. 30 августа я ехал на работу к 14:00, на выходе из метро Юго-Восточная на меня напали 2 чеченца ( https://www.m24.ru/shows1/14/308198 сюжет на Москва 24, правда они вырезали специально тот кусок, когда я отмахивался, разрывая дистанцию, уже после нескольких минут избиения в голову и назвали это “дракой”, хотя ни одного удара я не нанес), я подбежал к службе безопасности метрополитена, одна из сотрудниц сразу убежала, вторая стояла и смотрела как меня избивают, ничего не делая. В итоге мне сломали нос и нанесли множественные повреждения в области головы. Когда они меня били они орали, что они из Чечни и всех русских вы**ут и ничего им не сделают, явный состав 282 статьи УК РФ, однако в итоге им инкриминировали лишь 115. После их задержания, когда я ждал скорую, полицейская сказала, что у них был нож и они орали, что воевали против русских в чеченскую войну, а также что они находятся под действием наркотиков (в таганском отделении опер потом также сказал). После меня отвезли в ГКБ им. Пирогова, в приемное отделение к нейрохирургу, где я пробыл более 6 часов, как в последствии выяснилось, принял со скорой меня санитар, а заключение выдал медбрат. В итоге в заключении прописаны препараты, которые мне якобы ввели, но их не вводили + заключение противоречит в некоторых моментах самому себе. Госпитализировать меня отказались, хотя по словам врачей скорой должны были госпитализировать на 10-14 дней. На следующий день я пошел в травмпункт рядом с домом, чтобы снять всё-таки побои, но травматолог сказал, что поставил бы ушиб мягких тканей только в случае наличия разрыва кожи (хотя это уже должно быть рваной раной, в моём понимании).

На данном этапе мне не дали ознакомиться с материалами уголовного дела, нож по словам дознавательницы в деле не фигурирует, я просил ознакомить меня с записями с камер видеонаблюдения, мне было отказано, а также с дозоров полицейских, тоже было отказано. Дознавательница не присылает никаких повесток по следственным действиям, я посмотрел, её действия нарушают 164, 188 и 192 статьи УПК РФ, когда на очередной встрече я хотел написать заявление на отвод дознавателя. Я думаю, что дознавательница ангажирована к этим чеченцам и/или диаспоре. При первой встрече, назначенной на 10:00, она отказалась меня принять к оговоренному по телефону (повестки не было) времени, а когда из кабинета выходил другой сотрудник, я слышал, как она говорит кому-то из своих “мариную **анного терпилу”.

Прошу оказать юридическую помощь, что делать с этой дознавательницей? Что делать с врачами, которые отказались меня принимать и госпитализировать? Мне назначена очная ставка на 20 ноября, но я боюсь туда идти, потому что возможен вариант, что эти чеченцы придут туда с оружием.

Подбегая к сотрудникам безопасности метро, я включил камеру, думал это их вразумит, я стал кричать, что они хотят меня убить, но люди даже не обернулись. У меня сохранился кусочек видео, до того момента, как один из нападавших выхватил телефон (когда он выхватил телефон, то прервал запись) у меня из рук и начал меня избивать.

Что такое степень числа

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

4 — основание степени;
6 — показатель степени.

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Степенью числа « a » с натуральным показателем « n », бóльшим 1 , называется произведение « n » одинаковых множителей, каждый из которых равен числу « a ».

Запись « a n » читается так: « а в степени n » или « n -ая степень числа a ».

Исключение составляют записи:

a 2 — её можно произносить как « а в квадрате»;
a 3 — её можно произносить как « а в кубе».

Конечно, выражения выше можно читать и по определению степени:

a 2 — « а во второй степени»;
a 3 — « а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0) .

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

(−32) 0 = 1
0 253 = 0
1 4 = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

5 3 = 5 · 5 · 5 = 125
2,5 2 = 2,5 · 2,5 = 6,25
(
3
4
) 4 =
3
4
·
3
4
·
3
4
·
3
4
=
3 · 3 · 3 · 3
4 · 4 · 4 · 4
=
81
256

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Отрицательное число, возведённое в чётную степень, есть число положительное .

Отрицательное число, возведённое в нечётную степень, — число отрицательное .

Квадрат любого числа есть положительное число или нуль, то есть:

a 2 ≥ 0 при любом a .

2 · (−3) 2 = 2 · (−3) · (−3) = 2 · 9 = 18
−5 · (−2) 3 = −5 · (−8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

Возвести в четвёртую степень положительное число 5 .
5 4 = 5 · 5 · 5 · 5 = 625
Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
−5 4 = −625

Пример. Вычислить: −6 2 − (−1) 4

6 2 = 6 · 6 = 36
−6 2 = −36
(−1) 4 = (−1) · (−1) · (−1) · (−1) = 1
−(−1) 4 = −1
−36 − 1 = −37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление , а в конце сложение и вычитание .

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Числа. Степень числа.

Общеизвестный факт что сумму нескольких равных слагаемых можно найти с помощью умножения. Например : 5+5+5+5+5+5=5х6. О таком выражении говорят, что сумму равных слагаемых свернули в произведение. И наоборот, если читать это равенство справа налево, получаем, что мы развернули сумму равных слагаемых. Аналогично можно сворачивать произведение нескольких равных множителей 5х5х5х5х5х5=5 6 .

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».

Выражение 5 6 – это степенью числа, где:

5 – основание степени;

6 – показатель степени.

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

В общем виде степень с основанием “a” и показателем “n” записывается так

Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а

Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1

Если возвести число «а» возвести в первую степень, то получим само число a: a 1 = a

Если возвести любое число в нулевой степень, то в результате вычислений получим один . a 0 = 1

Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа, третью – кубом этого числа.

В степень можно возводить любое число – положительное, отрицательное или нуль. При этом не пользуются следующими правилами:

-при нахождении степени положительного числа получается положительное число.

-при вычислениях нуля в натуральной степени получаем ноль.

– при вычислении степени отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Если решить несколько примеров на вычисление степени отрицательных чисел, то получится, что если мы вычисляем нечётную степень отрицательного числа, то в результате будет число со знаком минус. Так как при умножении нечётного количество отрицательных сомножителей получаем отрицательное значение.

Если же мы рассчитываем четную степень для отрицательного числа, то в результате будет положительное число. Так как при умножении чётного количества отрицательных сомножителей получаем положительное значение.

Свойства степени с натуральным показателем.

Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:

например: 7 1.7 · 7 – 0.9 = 7 1.7+( – 0.9) = 7 1.7 – 0.9 = 7 0.8

Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:

например: 13 3.8 / 13 -0.2 = 13 (3.8 -0.2) = 13 3.6

При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.

например: (2 3 ) 2 = 2 3·2 = 2 6

Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель

например:(2·3) 3 = 2 n · 3 m ,

При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби

например: (2 / 5) 3 = (2 / 5) · (2 / 5) · (2 / 5) = 2 3 / 5 3 .

Последовательность выполнения расчетов при работе с выражениями содержащими степень.

При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.

Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.

Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.

Чему равно число в нулевой степени?

Доброго времени суток.

Обычно, когда мы возводим число в какую – либо степень, мы умножаем число на это же число столько раз, исходя из степени.

Так, если у нас есть 2 в квадрате, то мы 2 умножаем на 2 и получаем 4; если 2 в кубе, то 2 умножаем на 2 и потом еще раз на два и получаем 8 и тд.

А вот в случае с нулевой степенью мы не умножаем, а наоборот делим число на само число. Соответственно, результатом этого действия будет единица.

Итак, при возведении любого числа (кроме 0) в нулевую степень мы получим результат – единица.

Любое число в нулевой степени равно единице, потому что x^y/x^y = 1, а при делении, степени чисел вычитаются и степень, в данном случае, получается равной нулю.

5^2/5^2 = 5^(2-2) = 5^0 = 1

Курс начальной школы.

Из основных свойств нуля: при возведении любого числа в нулевую степень получаем 1.

Из свойств степеней:

если n=m=1, то уровень наглядности повышается.

Нулевая степень числа равна единице за исключением ноля.Это становится очень хорошо понятно, если посмотреть на следующий пример:

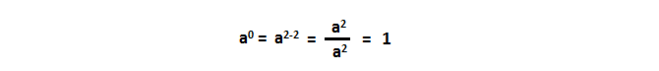
Ноль в нулевой степени в математике не имеет смысла, а если быть точнее – неопределен, хотя ноль в степени 1, 2, 3 и т.д всегда равен нолю.

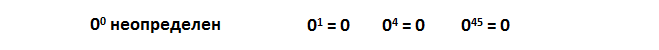
Любое отрицательное число при возведении в нулевую степень равно 1, но если минус стоит просто перед числом, тогда минус 1.

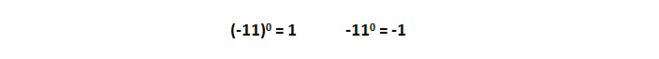
Любая дробь в нулевой степени равна 1, ведь ее всегда можно записать в виде, где числитель и знаменатель будут в нулевой степени.

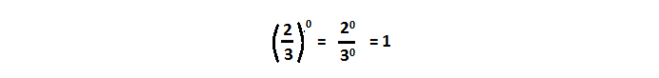
Число в нулевой степени всегда имеет результат – единицу, дробь тоже в нулевой степени будет равна единице, как и отрицательное число, ноль в нулевой степени – бессмысленное число. Задание легкое из школьного курса.

Какое бы число вы не пожелали возвести в нулевую степень результат будет равным единице. А если, к примеру говорить о возведении самого нуля, то в данном случае в какую бы степень вы не возводили ноль, значение всегда будет равно тому самому возводимому нулю.

Где-то читала объяснение, почему при возведении любого числа (кроме 0) в нулевую степень, в результате получается единица. Оно звучало так: получается, что мы как бы делим число на само себя. Поэтому, вообщем-то, не важно – какое число перед нами, целое или дробное. Что касается 0 (аксиома: на 0 делить нельзя), соответственно 0 в нулевой степени – да, не имеет смысла. Наглядно это выглядит примерно так:

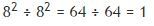
Все со школьной скамьи помнят правило, что любое число, кроме нуля, возведенное в нулевую степень, будет равно единице. Уж не знаю, как нашим учителям удалось так крепко убить в наши головы это правило, но видимо оно зацепило своей и гениальностью, и простотой. Ведь если попробовать разобраться, почему именно единице, то сложная схема говорит об элементарном решении.

Попробуем привести несколько примеров, чтобы наглядно увидеть решение:

Но это еще можно назвать сложным объяснением, так как самое легкое встречается как раз в школьном учебнике и проще наверно и не придумать

Поэтому видимо и запомнили навсегда, что число в нулевой степени равно единице.

Это несложное задание со школьных времён довольно просто запомнить каждому школьнику. Помню, что учительница говорила на эту тему нам в те времена. Если возводите какое бы то ни было числов нулевую степень в нулевую степень, то оно всегда будет иметь рсвоим итоговым результатом единицу. Ответ: единица.

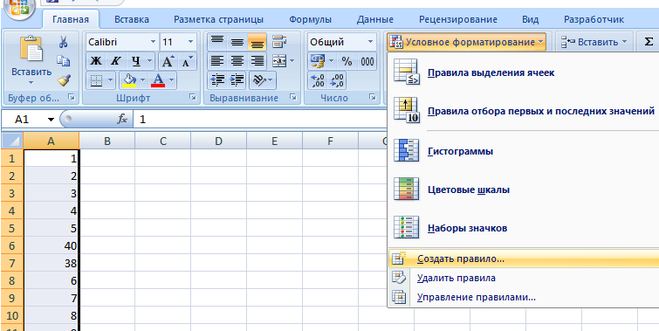
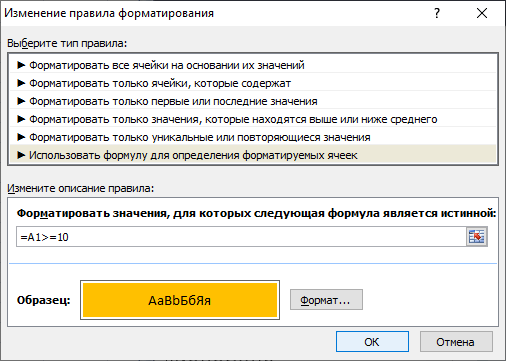
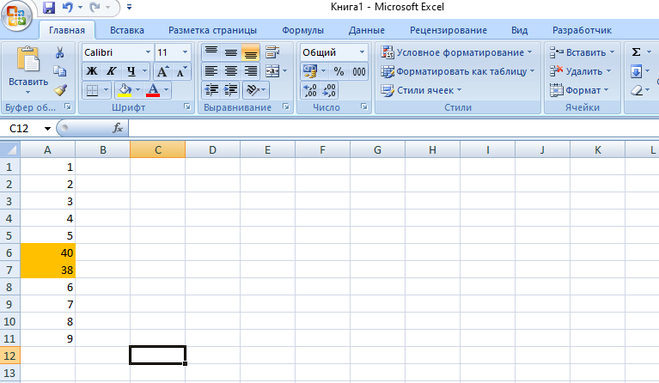
Чтобы выделить все числа из определённого диапазона по условию необходимо:

выделить этот диапазон
на вкладке “ГлавнаяСтили” нажать “Условное форматированиеСозда ть правило”

В данном неоднозначном вопросе отметился даже Коши и Бурбаки..

Но попробуем произвести своё доказательство..

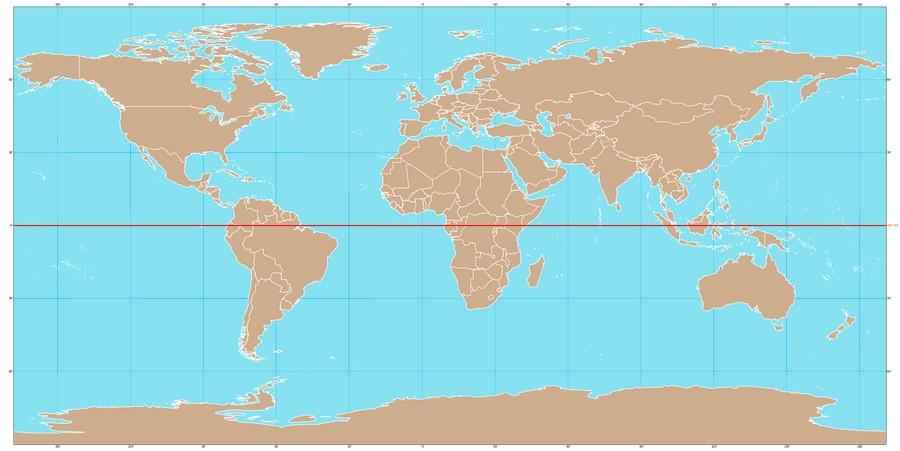
Если рассмотреть ряд степенных функций в первом квандранте, всё время увеличивая степень, то такая функция будет вырождаться в ступенчатую функцию..

При этом скачок будет равен 1..

На протяжении от нуля до единицы будет область начала скачка, т.е. координаты аргументов могут быть произвольными, тогда как функция будет равна 1.. Налицо будет неопределённость..

Теперь рассмотрим функции корней, что являются функциями в отрицательной степени, устремляя их показатель в бесконечность также приходим к скачкообразной функции, пр

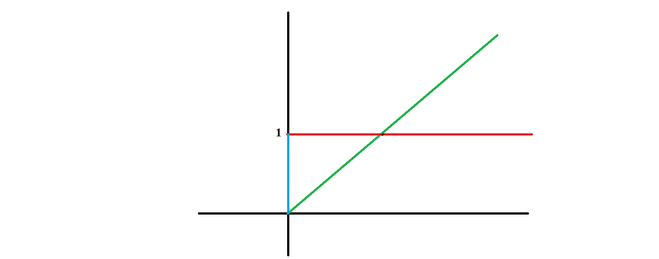
На рисунке красным обозначена предельная функция, в области фронта скачка (обозначено синим) имеется неопределённость..

Т.е. ноль в степени ноль – это неопределённость..

Есть еще такое объяснение

По этому правилу можно найти любой факториал, кроме (-1)!, потому что получится

(-1)! = 0! / 0 = 1 / 0 = oo

И поэтому факториалы от любых целых отрицательных чисел не определены.

А вот факториалы от нецелых чисел вполне определены, и означают как раз гамма-функцию, описанную Грустным Роджером.

Для целых х будет Г(x) = (x-1)!

А для нецелых х будет Г(x) = ʃ(0,oo) e^(-t) * t^(x-1) dt

Обрати внимание, что интеграл берется по переменной t, а функция зависит от х, который находится в показателе степени.

Сразу скажу – интеграл неберущийся, его нельзя выразить через обычные функции. Только численными методами!

даже если не считать ноль за число, нечетный и четных чисел будет поровну, если числовой ряд кончается на четное число. Самый простой пример: 1 2 3 4 5 6 7 8 9 10 – в этом ряду 5 четных и 5 нечетных чисел. Если числовой ряд кончается на нечетное число – тогда нечетных будет на 1 больше. Пример: 1 2 3 4 5 6 7 8 9 – 4 четных, 5 нечетных.

Когда мы рассматриваем числовой ряд от 1 до бесконечности, сама бесконечность не включает в себя понятия четного и нечетного числа – это именно бесконечно большое число. И количество четных-нечетных чисел в нем так же бесконечно большое. (из матана – бесконечность, деленное на любое целое число будет бесконечность. В данном случае делим на 2 – чередование четное-нечетное)Поэтому погрешностью (точнее, разницей) в 1 число можно пренебречь. Вот и получается, что фраза о том, что в бесконечном числовом ряду четных и нечетных чисел поровну.

Такие дроби называются ОБРАТНЫМИ. В произведении они дают единицу.

Число в нулевой степени

Число А в степени 0 = число А в степени (n – n) = (число А в степени n)/(число А в степени n) = 1. Извините, не могу применить редактор формул к текстам посланий в Спрашке. Число 0 в степени 0 = число 0 в степени (n – n) = (число 0 в степени n)/(число 0 в степени n) = бесконечность. Частное от деления делимого на 0 всегда равно бесконечности. Логарифм от единицы по любому основанию, кроме 0 равен 0. Число ноль в степени x равно 0 при условии, что x > 0. При x=0 или x 9 месяцев

Потому что так договорились некоторые математики. А другие с ними спорят и утверждают что ноль в нулевой степени есть неопределённость.. Споры идут до сих пор и единого мнения на этот счёт не существует.

Число А в степени 0 = число А в степени (n – n) = (число А в степени n)/(число А в степени n) = 1. Извините, не могу применить редактор формул к текстам посланий в Спрашке.

0 в степени 0 не равно 1, просто в некоторых случаях так удобно считать, потому что предел х в степени х при х стремящимся к 0 равен 1.

любое число в нулевой степени кроме нуля, равно единице. В точке 0 функция имеет неустранимый разрыв и определена быть не может

Для общности: возьмите график функции “Х в степени 0” – всюду прямая на уровне 1. Зачем же для одной точки делать исключение.

Привет Москвичу. И что мы не спим? Смотрю на подсвеченную в парке коломенском церковь. Красиво.

Вроде есть правило что любое число в нулевой степени равно единице.

Я знаю,что факториал 0 равен 1.а в степени в любой вроде так и будет 0

меня больше интересует вопрос. Где можно это знание применить?

При слове математика моя рука тянется к кобуре вальтера!

Для кого? Для меня это реальные ценности, моя реализация. Для Вас, возможно, ценности глобальные, но это Ваши ценности.

Вот именно, что прежде всего нужно понимать и признавать то что ценности могут быть разные у разных людей. И твои ценности не являются для всех едиными и единственно важными. Возможно совершенно наоборот, именно твоё для других будет самым ничтожным и ничего не значащим.
Уважай чужие ценности, отличные от других. И понимай что твои не имеют никакого приоритета для других.

Ценности порождаются разумом, и распространяются как идеи. Потому это то что требует доказательств и убеждения. И то, лишь те что создают выгоды, помогают и дают преимущества, в итоге побеждают. Конкуренция ценностей имеет такие же механизмы как и любая другая.

Эко Вас. т.е. вы такой замечательный о человечестве думаете? О каких ценностях идёт речь? Коммунистических, капиталистических? Вы определитесь. В России за 100 лет всё менялось ни один раз. Большевички жён хотели сделать общими. Теперь о уважении. Т.к. Вы мои ценности даже рассматривать не хотите, то убедите меня, что Ваши ценности ( о коих Вы умалчиваете) для меня имеют значение и я должен (понятие сие мне чуждо-я никому ничего не должен) их уважать. И еще-вопрос был “0 в степени 0=1”,т.е. о математике. Причём здесь ценности?

Вот видишь, оценка исходя из собственных ценностей и уровня знаний)
Я просто скажу, что одна из основных правовых характеристик Человека, обладающего правами и свободами, обязательная забота о человечестве в целом) Рассматривание всех проблем как глобальных. Примерно такое же, как и классическое определение гуманиста, настоящего, древнегреческого)) Иначе мы не имеем Человека, со всеми вытекающими правовыми последствиями)
Это конкретное условие.

На уровне закона, если так понятнее))

Раб всегда всё делит на белое или черное, хорошее или плохое, доброе или злое. Стремиться примкнуть ка какой-нибудь стороне. Он несвободен в своих взглядах, не способен к обобщениям, к взгляду на весь мир, на всё человечества.

Это тоже конкретная определяющая права характеристика раба) Одна из.

И всё определяет осознанность. Разумность. Способность принять и понять эти основы определяющие разумность, дееспособность и адекватность любого.

Нет равенства. Его не бывает. Люди разные. И нельзя допускать к принятию решений откровенных животных и клинических идиотов))

И мне не интересны ваши ценности, потому что вы уже показали ваш уровень понимания этого мира) и отношения к нему. Показали ваш правовой статус.

Психиатрические отклонения на лицо, да еще и не воспитан. Я Вам не тыкал. А то что Вы “сплагиатили” на Вашей совести.

по курсу нацбанка, ну сколько в нуле нулей, один конечно

потому что нет абсолютного 0. Всегда в минус или в плюс.

Потому что предел Х в степени Х при Х стремящимся к 0 = 1

Схождение бесконечностей даёт начало отсчёта? Ого!

Степень числа: определения, обозначение, примеры

В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.

Степени с натуральными показателями: понятие квадрата и куба числа

Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).

Степень числа a с натуральным показателем n – это произведение n -ного числа множителей, каждый из которых равен числу а . Записывается степень так: a n , а в виде формулы ее состав можно представить следующим образом: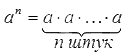

Например, если показатель степени равен 1 , а основание – a , то первая степень числа a записывается как a 1 . Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a 1 = a .

В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида 8 · 8 · 8 · 8 можно сократить до 8 4 . Примерно так же произведение помогает нам избежать записи большого числа слагаемых ( 8 + 8 + 8 + 8 = 8 · 4 ) ; мы это уже разбирали в статье, посвященной умножению натуральных чисел.

Как же верно прочесть запись степени? Общепринятый вариант – « a в степени n ». Или можно сказать « n -ная степень a » либо « a n -ной степени». Если, скажем, в примере встретилась запись 8 12 , мы можем прочесть « 8 в 12 -й степени», « 8 в степени 12 » или « 12 -я степень 8 -ми».

Вторая и третья степени числа имеют свои устоявшиеся названия: квадрат и куб. Если мы видим вторую степень, например, числа 7 ( 7 2 ) , то мы можем сказать « 7 в квадрате» или «квадрат числа 7 ». Аналогично третья степень читается так: 5 3 – это «куб числа 5 » или « 5 в кубе». Впрочем, употреблять стандартную формулировку «во второй/третьей степени» тоже можно, это не будет ошибкой.

Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.

В основании не обязательно должно стоять целое число: для степени ( 4 , 32 ) 9 основанием будет дробь 4 , 32 , а показателем – девятка. Обратите внимание на скобки: такая запись делается для всех степеней, основания которых отличаются от натуральных чисел.

Например: 1 2 3 , ( – 3 ) 12 , – 2 3 5 2 , 2 , 4 35 5 , 7 3 .

Для чего нужны скобки? Они помогают избежать ошибок в расчетах. Скажем, у нас есть две записи: ( − 2 ) 3 и − 2 3 . Первая из них означает отрицательное число минус два, возведенное в степень с натуральным показателем три; вторая – число, соответствующее противоположному значению степени 2 3 .

Иногда в книгах можно встретить немного другое написание степени числа – a ^ n (где а – основание, а n – показатель). То есть 4 ^ 9 – это то же самое, что и 4 9 . В случае, если n представляет собой многозначное число, оно берется в скобки. Например, 15 ^ ( 21 ) , ( − 3 , 1 ) ^ ( 156 ) . Но мы будем использовать обозначение a n как более употребительное.

О том, как вычислить значение степени с натуральным показателем, легко догадаться из ее определения: нужно просто перемножить a n -ное число раз. Подробнее об этом мы писали в другой статье.

Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.

Что такое степени с целым показателем

В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.

Степень числа с целым положительным показателем можно отобразить в виде формулы: .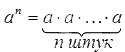

При этом n – любое целое положительное число.

Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:

Равенство a m : a n = a m − n будет верно при условиях: m и n – натуральные числа, m n , a ≠ 0 .

Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0

Но при этом a n : a n = 1 – частное равных чисел a n и a . Выходит, что нулевая степень любого отличного от нуля числа равна единице.

Однако такое доказательство не подходит для нуля в нулевой степени. Для этого нам нужно другое свойство степеней – свойство произведений степеней с равными основаниями. Оно выглядит так: a m · a n = a m + n .

Если n у нас равен 0 , то a m · a 0 = a m (такое равенство также доказывает нам, что a 0 = 1 ). Но если а также равно нулю, наше равенство приобретает вид 0 m · 0 0 = 0 m , Оно будет верным при любом натуральном значении n , и неважно при этом, чему именно равно значение степени 0 0 , то есть оно может быть равно любому числу, и на верность равенства это не повлияет. Следовательно, запись вида 0 0 своего особенного смысла не имеет, и мы не будем ему его приписывать.

При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.

Разберем пример с конкретными числами: Так, 5 0 – единица, ( 33 , 3 ) 0 = 1 , – 4 5 9 0 = 1 , а значение 0 0 не определено.

После нулевой степени нам осталось разобраться, что из себя представляет степень отрицательная. Для этого нам понадобится то же свойство произведения степеней с равными основаниями, которое мы уже использовали выше: a m · a n = a m + n .

Введем условие: m = − n , тогда a не должно быть равно нулю. Из этого следует, что a − n · a n = a − n + n = a 0 = 1 . Выходит, что a n и a − n у нас являются взаимно обратными числами.

В итоге a в целой отрицательной степени есть не что иное, как дробь 1 a n .

Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).

Степень a с целым отрицательным показателем n можно представить в виде дроби 1 a n . Таким образом, a – n = 1 a n при условии a ≠ 0 и n – любое натуральное число.

Проиллюстрируем нашу мысль конкретными примерами:

3 – 2 = 1 3 2 , ( – 4 . 2 ) – 5 = 1 ( – 4 . 2 ) 5 , 11 37 – 1 = 1 11 37 1

В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:

Степень числа a с натуральным показателем z – это: a z = a z , e с л и z – ц е л о е п о л о ж и т е л ь н о е ч и с л о 1 , z = 0 и a ≠ 0 , ( п р и z = 0 и a = 0 п о л у ч а е т с я 0 0 , з н а ч е н и я в ы р а ж е н и я 0 0 н е о п р е д е л я е т с я ) 1 a z , е с л и z – ц е л о е о т р и ц а т е л ь н о е ч и с л о и a ≠ 0 ( е с л и z – ц е л о е о т р и ц а т е л ь н о е ч и с л о и a = 0 п о л у ч а е т с я 0 z , е г о з н а ч е н и е н е о п р е д е л я е т с я )

Что такое степени с рациональным показателем

Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.

Что такое рациональные числа? В их множество входят как целые, так и дробные числа, при этом дробные числа можно представить в виде обыкновенных дробей (как положительных, так и отрицательных). Сформулируем определение степени числа a с дробным показателем m / n , где n – натуральное число, а m – целое.

У нас есть некоторая степень с дробным показателем a m n . Для того, чтобы свойство степени в степени выполнялось, равенство a m n n = a m n · n = a m должно быть верным.

Учитывая определение корня n -ной степени и что a m n n = a m , мы можем принять условие a m n = a m n , если a m n имеет смысл при данных значениях m , n и a .

Приведенные выше свойства степени с целым показателем будут верными при условии a m n = a m n .

Основной вывод из наших рассуждений таков: степень некоторого числа a с дробным показателем m / n – это корень n -ой степени из числа a в степени m . Это справедливо в том случае, если при данных значениях m , n и a выражение a m n сохраняет смысл.

Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.

1. Мы можем ограничить значение основания степени: возьмем a , которое при положительных значениях m будет больше или равно 0 , а для отрицательных – строго меньше (поскольку при m ≤ 0 мы получаем 0 m , а такая степень не определена). В таком случае определение степени с дробным показателем будет выглядеть следующим образом:

Степень с дробным показателем m / n для некоторого положительного числа a есть корень n -ной степени из a, возведенного в степень m . В виде формулы это можно изобразить так:

Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.

Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как

0 m n = 0 m n = 0 при условии целого положительного m и натурального n .

При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.

Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.

Выражение a m n иногда все же имеет смысл при некоторых отрицательных значениях a и некоторых m . Так, верны записи ( – 5 ) 2 3 , ( – 1 , 2 ) 5 7 , – 1 2 – 8 4 , в которых основание отрицательно.

2. Второй подход – это рассмотреть отдельно корень a m n с четными и нечетными показателями. Тогда нам потребуется ввести еще одно условие: степень a , в показателе которой стоит сократимая обыкновенная дробь, считается степенью a , в показателе которой стоит соответствующая ей несократимая дробь. Позже мы объясним, для чего нам это условие и почему оно так важно. Таким образом, если у нас есть запись a m · k n · k , то мы можем свести ее к a m n и упростить расчеты.

Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.

Объединим все данные выше определения в одной записи:

Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.

Для любой обыкновенной сократимой дроби m · k n · k степень можно заменить на a m n .

Степень числа a с несократимым дробным показателем m / n – можно выразить в виде a m n в следующих случаях: – для любых действительных a , целых положительных значений m и нечетных натуральных значений n . Пример: 2 5 3 = 2 5 3 , ( – 5 , 1 ) 2 7 = ( – 5 , 1 ) – 2 7 , 0 5 19 = 0 5 19 .

– для любых отличных от нуля действительных a , целых отрицательных значений m и нечетных значений n , например, 2 – 5 3 = 2 – 5 3 , ( – 5 , 1 ) – 2 7 = ( – 5 , 1 ) – 2 7

– для любых неотрицательных a , целых положительных значений m и четных n , например, 2 1 4 = 2 1 4 , ( 5 , 1 ) 3 2 = ( 5 , 1 ) 3 , 0 7 18 = 0 7 18 .

– для любых положительных a , целых отрицательных m и четных n , например, 2 – 1 4 = 2 – 1 4 , ( 5 , 1 ) – 3 2 = ( 5 , 1 ) – 3 , .

В случае других значений степень с дробным показателем не определяется. Примеры таких степеней: – 2 11 6 , – 2 1 2 3 2 , 0 – 2 5 .

Теперь объясним важность условия, о котором говорили выше: зачем заменять дробь с сократимым показателем на дробь с несократимым. Если бы мы этого не сделали бы, то получились бы такие ситуации, скажем, 6 / 10 = 3 / 5 . Тогда должно быть верным ( – 1 ) 6 10 = – 1 3 5 , но – 1 6 10 = ( – 1 ) 6 10 = 1 10 = 1 10 10 = 1 , а ( – 1 ) 3 5 = ( – 1 ) 3 5 = – 1 5 = – 1 5 5 = – 1 .

Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.

Таким образом, степень положительного числа a с дробным показателем m / n определяется как 0 m n = 0 m n = 0 . В случае отрицательных a запись a m n не имеет смысла. Степень нуля для положительных дробных показателей m / n определяется как 0 m n = 0 m n = 0 , для отрицательных дробных показателей мы степень нуля не определяем.

В выводах отметим, что можно записать любой дробный показатель как в виде смешанного числа, так и в виде десятичной дроби: 5 1 , 7 , 3 2 5 – 2 3 7 .

При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:

5 1 , 7 = 5 17 10 = 5 7 10 3 2 5 – 2 3 7 = 3 2 5 – 17 7 = 3 2 5 – 17 7

Что такое степени с иррациональным и действительным показателем

Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.

Допустим, что у нас есть иррациональное число a и последовательность его десятичных приближений a 0 , a 1 , a 2 , . . . . Например, возьмем значение a = 1 , 67175331 . . . , тогда

a 0 = 1 , 6 , a 1 = 1 , 67 , a 2 = 1 , 671 , . . . , a 0 = 1 , 67 , a 1 = 1 , 6717 , a 2 = 1 , 671753 , . . .

и так далее (при этом сами приближения являются рациональными числами).

Последовательности приближений мы можем поставить в соответствие последовательность степеней a a 0 , a a 1 , a a 2 , . . . . Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней.

Возьмем для примера a = 3 , тогда a a 0 = 3 1 , 67 , a a 1 = 3 1 , 6717 , a a 2 = 3 1 , 671753 , . . . и т.д.

Последовательность степеней можно свести к числу, которое и будет значением степени c основанием a и иррациональным показателем a . В итоге : степень с иррациональным показателем вида 3 1 , 67175331 . . можно свести к числу 6 , 27 .

Степень положительного числа a с иррациональным показателем a записывается как a a . Его значение – это предел последовательности a a 0 , a a 1 , a a 2 , . . . , где a 0 , a 1 , a 2 , . . . являются последовательными десятичными приближениями иррационального числа a . Степень с нулевым основанием можно определить и для положительных иррациональных показателей, при этом 0 a = 0 Так, 0 6 = 0 , 0 21 3 3 = 0 . А для отрицательных этого сделать нельзя, поскольку, например, значение 0 – 5 , 0 – 2 π не определено. Единица, возведенная в любую иррациональную степень, остается единицей, например, и 1 2 , 1 5 в 2 и 1 – 5 будут равны 1 .