Обыкновенные дроби
О чем эта статья:
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2.
- Треть — одна третья доля предмета или 1/3.
- Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Виды дробей:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 – 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x – y). Значение дроби зависит от данных значений букв.
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
где a, b, k — натуральные числа.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
- В обеих дробях знаменатель равен 5.
- В первой дроби числитель равен 1, во второй дроби равен 4.
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
- Приведем дроби к общему знаменателю:
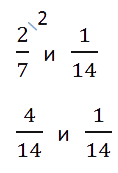
- Сравним дроби с одинаковыми знаменателями:
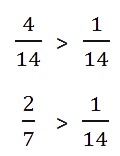
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к наименьшему общему знаменателю (НОЗ);
- сравнить полученные дроби.
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
- Найти наименьшее общее кратное (НОК) знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
- Найдем наименьшее общее кратное для определения единого делителя.
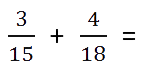
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
Полученные числа запишем справа сверху над числителем.
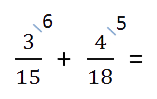
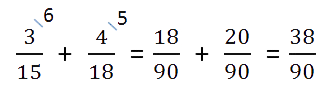
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
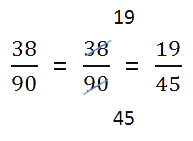
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.
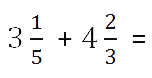
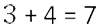
- Сложить дробные части.
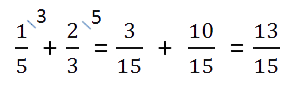
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
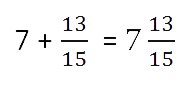
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- если получилась неправильная дробь, преобразовать в смешанную.
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
- знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
- представить числа в виде неправильных дробей;
- разделить то, что получилось друг на друга.
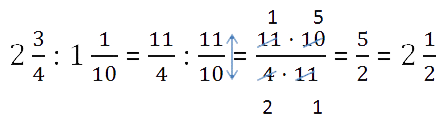
ОБЫКНОВЕННАЯ ДРОБЬ
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.
Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.
Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
- Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к наименьшему общему знаменателю;
- сравнить полученные дроби.
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
- найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
- разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.
Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!
Общий случай сложения (вычитания) дробей.
Умножение дробей
- Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
- При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.
Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.
При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.
Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Десятичная дробь
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Обыкновенная (простая) дробь. Числитель и знаменатель дроби.
Правильная и неправильная дробь. Смешанное число.
Неполное частное. Целая и дробная часть. Обратные дроби.
Часть единицы или несколько её частей называются обыкновенной или простой дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей – числителем. Дробь записывается в виде:
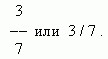
Здесь 3 – числитель, 7 – знаменатель.
Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью. Если числитель равен знаменателю, то дробь равна 1. Если числитель больше знаменателя, то дробь больше 1. В обоих последних случаях дробь называется неправильной. Если числитель делится на знаменатель, то эта дробь равна частному от деления: 63 / 7 = 9. Если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом:
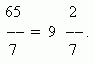
Здесь 9 – неполное частное (целая часть смешанного числа), 2 – остаток (числитель дробной части), 7 – знаменатель.
Часто бывает необходимо решать обратную задачу – обратить смешанное число в дробь . Для этого умножаем целую часть смешанного числа на знаменатель и прибавляем числитель дробной части. Это будет числитель обыкновенной дроби, а знаменатель остаётся прежним.
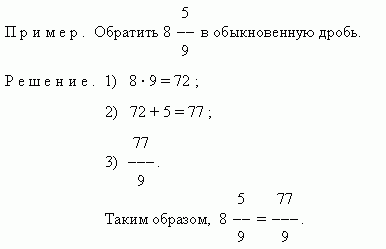
Обратные дроби – это две дроби, произведение которых равно 1. Например, 3 / 7 и 7 / 3 ; 15 / 1 и 1 / 15 и т.д.
Действия с обыкновенными дробями
Расширение дроби. Сокращение дроби. Сравнение дробей.
Приведение к общему знаменателю. Сложение и вычитание дробей.
Умножение дробей. Деление дробей.
Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется расширением дроби. Например,
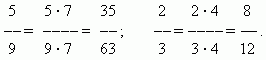
Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется сокращением дроби. Например,
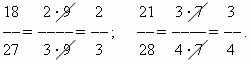
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:
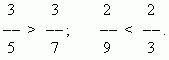
Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:
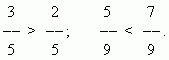
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.
П р и м е р . Сравнить две дроби:
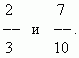
Использованное здесь преобразование называется приведением дробей к общему знаменателю.
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
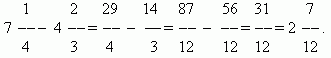
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.
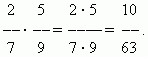
Деление дробей. Для того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь . Это правило вытекает из определения деления (см. раздел “Арифметические операции”).
П р и м е р .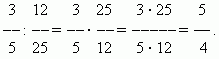 
Доли, обыкновенные дроби: определения, обозначения, примеры, действия с дробями
Рассмотрение данной темы мы начнем с изучения понятия доли в целом, которое даст нам более полное понимание смысла обыкновенной дроби. Дадим основные термины и их определение, изучим тему в геометрическом толковании, т.е. на координатной прямой, а также определим список основных действий с дробями.
Доли целого
Представим некий предмет, состоящий из нескольких, совершенно равных частей. Например, это может быть апельсин, состоящий из нескольких одинаковых долек.
Доля целого или доля – это каждая из равных частей, составляющих целый предмет.
Очевидно, что доли могут быть разные. Чтобы наглядно пояснить это утверждение, представим два яблока, одно из которых разрезано на две равные части, а второе – на четыре. Ясно, что размеры получившихся долей у разных яблок будут различаться.
Доли имеют свои названия, которые зависят от количества долей, составляющих целый предмет. Если предмет имеет две доли, то каждая из них будет определяться как одна вторая доля этого предмета; когда предмет состоит из трех долей, то каждая из них – одна третья и так далее.
Половина – одна вторая доля предмета.
Треть – одна третья доля предмета.
Четверть – одна четвертая доля предмета.
Чтобы сократить запись, ввели следующие обозначения долей: половина – 1 2 или 1 / 2 ; треть – 1 3 или 1 / 3 ; одна четвертая доля – 1 4 или 1 / 4 и так далее. Записи с горизонтальной чертой используются чаще.
Понятие доли естественно расширяется с предметов на величины. Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.
Обыкновенные дроби, определение и примеры
Обыкновенные дробиприменяются для описания количества долей. Рассмотрим простой пример, который приблизит нас к определению обыкновенной дроби.
Представим апельсин, состоящий из 12 долек. Каждая доля тогда будет – одна двенадцатая или 1 / 12 . Две доли – 2 / 12 ; три доли – 3 / 12 и т.д. Все 12 долей или целое число будет выглядеть так: 12 / 12 . Каждая из используемых в примере записей является примером обыкновенной дроби.
Обыкновенная дробь – это запись вида m n или m / n , где m и n являются любыми натуральными числами.
Согласно данному определению, примерами обыкновенных дробей могут быть записи: 4 / 9 , 11 34 , 917 54 . А такие записи: 11 5 , 1 , 9 4 , 3 не являются обыкновенными дробями.
Числитель и знаменатель
Числителем обыкновенной дроби m n или m / n является натуральное число m .
Знаменателем обыкновенной дроби m n или m / n является натуральное число n .
Т.е. числитель – число, расположенное сверху над чертой обыкновенной дроби (или слева от наклонной черты), а знаменатель – число, расположенное под чертой (справа от наклонной черты).
Какой же смысл несут в себе числитель и знаменатель? Знаменатель обыкновенной дроби указывает на то, из скольких долей состоит один предмет, а числитель дает нам информацию о том, каково рассматриваемое количество таких долей. К примеру, обыкновенная дробь 7 54 указывает нам на то, что некий предмет состоит из 54 долей, и для рассмотрения мы взяли 7 таких долей.
Натуральное число как дробь со знаменателем 1
Знаменатель обыкновенной дроби может быть равен единице. В таком случае возможно говорить, что рассматриваемый предмет (величина) неделим, являет собой нечто целое. Числитель в подобной дроби укажет, какое количество таких предметов взято, т.е. обыкновенная дробь вида m 1 имеет смысл натурального числа m . Это утверждение служит обоснованием равенства m 1 = m .
Запишем последнее равенство так: m = m 1 . Оно даст нам возможность любое натуральное число использовать в виде обыкновенной дроби. К примеру, число 74 – это обыкновенная дробь вида 74 1 .
Любое натуральное число m возможно записать в виде обыкновенной дроби, где знаменатель – единица: m 1 .
В свою очередь, любая обыкновенная дробь вида m 1 может быть представлена натуральным числом m .
Черта дроби как знак деления
Использованное выше представление данного предмета как n долей является не чем иным, как делением на n равных частей. Когда предмет разделен на n частей, мы имеем возможность разделить его поровну между n людьми – каждый получит свою долю.
В случае, когда мы изначально имеем m одинаковых предметов (каждый разделен на n частей), то и эти m предметов возможно поровну разделить между n людьми, дав каждому из них по одной доле от каждого из m предметов. При этом у каждого человека будет m долей 1 n , а m долей 1 n даст обыкновенную дробь m n . Следовательно, обыкновенную дробь m n можно использовать, чтобы обозначать деление m предметов между n людьми.
Полученное утверждение устанавливает связь между обыкновенными дробями и делением. И эту связь можно выразить следующим образом: черту дроби возможно иметь в виду в качестве знака деления, т.е. m / n = m : n .
При помощи обыкновенной дроби мы можем записать итог деления двух натуральных чисел. К примеру, деление 7 яблок на 10 человек запишем как 7 10 : каждому человеку достанется семь десятых долей.
Равные и неравные обыкновенные дроби
Логичным действием является сравнение обыкновенных дробей, ведь очевидно, что, к примеру, 1 8 яблока отлична от 7 8 .
Результатом сравнения обыкновенных дробей может быть: равны или неравны.
Равные обыкновенные дроби – обыкновенные дроби a b и c d , для которых справедливо равенство: a · d = b · c .
Неравные обыкновенные дроби – обыкновенные дроби a b и c d , для которых равенство: a · d = b · c не является верным.
Пример равных дробей: 1 3 и 4 12 – поскольку выполняется равенство 1 · 12 = 3 · 4 .
В случае, когда выясняется, что дроби не являются равными, обычно необходимо также узнать, какая из данных дробей меньше, а какая – больше. Чтобы дать ответ на эти вопросы, обыкновенные дроби сравнивают, приводя их к общему знаменателю и затем сравнив числители.
Дробные числа
Каждая дробь – это запись дробного числа, что по сути – просто «оболочка», визуализация смысловой нагрузки. Но все же для удобства мы объединяем понятия дроби и дробного числа, говоря просто – дробь.
Дроби на координатном луче
Все дробные числа, как и любое другое число, имеют свое уникальное месторасположение на координатном луче: существует однозначное соответствие между дробями и точками координатного луча.
Чтобы на координатном луче найти точку, обозначающую дробь m n , необходимо от начала координат отложить в положительном направлении m отрезков, длина каждого из которых составит 1 n долю единичного отрезка. Отрезки можно получить, разделив единичный отрезок на n одинаковых частей.
Как пример, обозначим на координатном луче точку М , которая соответствует дроби 14 10 . Длина отрезка, концами которого является точка О и ближайшая точка, отмеченная маленьким штрихом, равна 1 10 доле единичного отрезка. Точка, соответствующая дроби 14 10 , расположена в удалении от начала координат на расстояние 14 таких отрезков.
Если дроби равны, т.е. им соответствует одно и то же дробное число, тогда эти дроби служат координатами одной и той же точки на координатном луче. К примеру, координатам в виде равных дробей 1 3 , 2 6 , 3 9 , 5 15 , 11 33 соответствует одна и та же точка на координатном луче, располагающаяся на расстоянии трети единичного отрезка, отложенного от начала отсчета в положительном направлении.
Здесь работает тот же принцип, что и с целыми числами: на горизонтальном, направленном вправо координатном луче точка, которой соответствует большая дробь, разместится правее точки, которой соответствует меньшая дробь. И наоборот: точка, координата которой – меньшая дробь, будет располагаться левее точки, которой соответствует бОльшая координата.
Правильные и неправильные дроби, определения, примеры
В основе разделения дробей на правильные и неправильные лежит сравнение числителя и знаменателя в пределах одной дроби.
Правильная дробь – это обыкновенная дробь, в которой числитель меньше, чем знаменатель. Т.е., если выполняется неравенство m n , то обыкновенная дробь m n является правильной.
Неправильная дробь – это обыкновенная дробь, числитель которой больше или равен знаменателю. Т.е., если выполняется неравенство undefined , то обыкновенная дробь m n является неправильной.
Обыкновенные дроби. Конспект
Из этой статьи вы узнаете:
1 Что такое обыкновенные дроби. Виды дробей.
Дробь всегда означает какую то часть целого. Дело в том, что не всегда количество можно передать натуральными числами, то есть пересчитать: 1,2,3 и т.д. Как, например, обозначить половину арбуза или четверть часа? Вот для этого и появились дробные числа, или дроби.
Для начала нужно сказать, что вообще дробей бывает два вида: обыкновенные дроби и десятичные дроби. Обыкновенные дроби записываются так:
Десятичные дроби записываются по другому:
Обыкновенные дроби состоят из двух частей: вверху — числитель, внизу — знаменатель. Числитель и знаменатель разделяет дробная черта. Итак, запомните:
Любая дробь — это часть целого. За целое обычно принимают 1 (единицу). Знаменатель дроби показывает, на сколько частей разделили целое (1), а числитель — сколько частей взяли. Если мы разрезали торт на 6 одинаковых частей ( в математике говорят долей ), то каждая часть торта будет равна 1/6. Если Вася съел 4 куска, то значит, он съел 4/6 .
С другой стороны, дробная черта — это не что иное, как знак деления. Поэтому дробь — это частное двух чисел — числителя и знаменателя. В тексте задач или в рецептах блюд дроби записываются обычно так: 2/3, 1/2 и т.д. Некоторые дроби получили собственное название, например, 1/2 — «половина», 1/3 — «треть», 1/4 — «четверть»
А теперь разберемся, какие бывают виды обыкновенных дробей.
2 Виды обыкновенных дробей
Обыкновенные дроби бывают трех видов: правильные, неправильные и смешанные:
Правильная дробь
Если числитель меньше, чем знаменатель, то такую дробь называют правильной, например: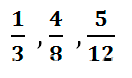 
Правильная дробь всегда меньше 1.
Неправильная дробь
Если числитель больше, чем знаменатель или равен знаменателю, такая дробь называется неправильной, например:
Неправильная дробь больше единицы(если числитель больше знаменателя) или равна единице (если числитель равен знаменателю)
Смешанная дробь
Если дробь состоит из целого числа (целая часть) и правильной дроби (дробная часть), то такая дробь называется смешанной, например: 
Смешанная дробь всегда больше единицы.
3 Преобразования дробей
В математике обыкновенные дроби часто приходится преобразовывать, то есть смешанную дробь превращать в неправильную и наоборот. Это необходимо для выполнения некоторых действий, например, умножения и деления.
Итак, любую смешанную дробь можно перевести в неправильную. Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:
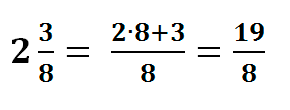
Любую неправильную дробь можно превратить в смешанную. Для этого делят числитель на знаменатель (с остатком).Полученное число будет целой частью, а остаток — числителем дробной части, например:
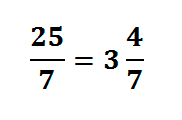
При этом говорят: «Мы выделили целую часть из неправильной дроби».
Необходимо запомнить еще одно правило: Любое целое число можно представить в виде обыкновенной дроби со знаменателем 1, например:
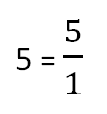
Поговорим о том, как сравнивать дроби.
4 Сравнение дробей
При сравнении дробей может быть несколько вариантов: Легко сравнивать дроби с одинаковыми знаменателями, гораздо сложнее — если знаменатели разные. А есть еще и сравнение смешанных дробей. Но не волнуйтесь, сейчас мы подробно рассмотрим каждый вариант и научимся сравнивать дроби.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями, но разными числителями больше та дробь, у которой числитель больше, например:
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями, но разными знаменателями больше та дробь, у которой знаменатель меньше, например:
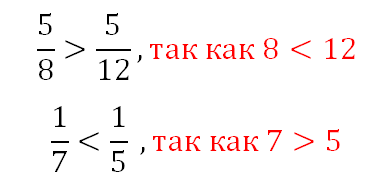
Сравнение смешанных и неправильных дробей с правильными дробями
Неправильная или смешанная дробь всегда больше правильной дроби, например:
Сравнение двух смешанных дробей
При сравнении двух смешанных дробей больше та дробь, у которой целая часть больше, например:
Если целые части у смешанных дробей одинаковые, больше та дробь, у которой дробная часть больше, например:
Сравнение дробей с разными числителями и знаменателями
Сравнивать дроби с разными числителями и знаменателями без их преобразования нельзя. Сначала дроби нужно привести к одному знаменателю, а затем сравнить их числители. Больше та дробь, у которой числитель будет больше. А вот как приводить дроби к одинаковому знаменателю, мы рассмотрим в следующих двух разделах статьи статьи. Сначала мы рассмотрим основное свойство дроби и сокращение дробей, а затем непосредственно приведение дробей к одному знаменателю.
5 Основное свойство дроби. Сокращение дробей. Понятие о НОД.
Запомните: складывать и вычитать, а также сравнивать можно только дроби, у которых одинаковые знаменатели. Если знаменатели разные, то сначала нужно привести дроби к одному знаменателю, то есть так преобразовать одну из дробей, чтобы ее знаменатель стал таким же, как у второй дроби.
У дробей есть одно важное свойство, называемое также основным свойством дроби:
Если и числитель, и знаменатель дроби умножить или разделить на одно и то же число, то величина дроби при этом не изменится:
Благодаря этому свойству мы можем сокращать дроби:
Сократить дробь — значит разделить и числитель, и знаменатель на одно и то же число(смотрите пример чуть выше). Когда мы сокращаем дробь, то можно расписать наши действия так:
Чаще же в тетради сокращают дробь так:
Но запомните: сокращать можно только множители. Если в числителе или знаменателе сумма или разность, сокращать слагаемые нельзя. Пример:
Нужно сначала преобразовать сумму в множитель:
Иногда, при работе с большими числами, для того, чтобы сократить дробь, удобно найти наибольший общий делитель числителя и знаменателя (НОД)
Наибольший общий делитель (НОД) нескольких чисел — это наибольшее натуральное число, на которое эти числа делятся без остатка.
Для того, чтобы найти НОД двух чисел (например, числителя и знаменателя дроби), нужно разложить оба числа на простые множители, отметить одинаковые множители в обоих разложениях, и перемножить эти множители. Полученное произведение и будет НОД. Например, нам нужно сократить дробь:
Найдем НОД чисел 96 и 36:
НОД нам показывает, что и в числителе, и в знаменателе есть множитель12, и мы легко сокращаем дробь.
Иногда, чтобы привести дроби к одному знаменателю, достаточно сократить одну из дробей. Но чаще бывает необходимо подбирать дополнительные множители для обеих дробей .Сейчас мы рассмотрим, как это делается. Итак:
6 Как приводить дроби к одному знаменателю. Наименьшее общее кратное (НОК).
Когда мы приводим дроби к одинаковому знаменателю, мы подбираем для знаменателя такое число, которое бы делилось и на первый, и на второй знаменатель (то есть было бы кратным обоим знаменателям, выражаясь математическим языком). И желательно, чтобы число это было как можно меньшим, так удобнее считать. Таким образом, мы должны найти НОК обоих знаменателей.
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
Однако вернемся к нашим дробям. После того, как мы подобрали или письменно вычислили НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители. Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом мы привели наши дроби к одному знаменателю — 15.
7 Сложение и вычитание дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Сложение и вычитание смешанных дробей с одинаковыми знаменателями
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью:
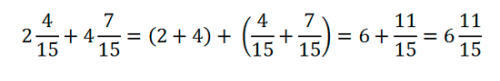
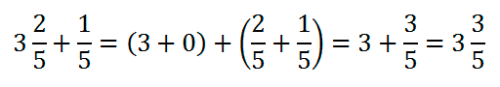
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
Вычитание проводится аналогично: целая часть вычитается из целой, а дробная — из дробной части: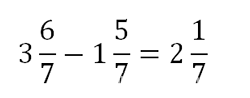
Если дробная часть вычитаемого больше, чем дробная часть уменьшаемого, «занимаем» единицу из целой части, превращая уменьшаемое в неправильную дробь, а дальше действуем как обычно: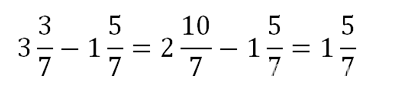
Аналогично вычитаем из целого числа дробь:
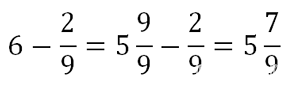
Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:
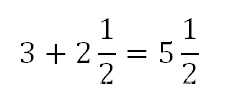
Сложение и вычитание дробей с разными знаменателями.
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как при сложении дробей с одинаковыми знаменателями (сложить числители):
При вычитании действуем аналогично:
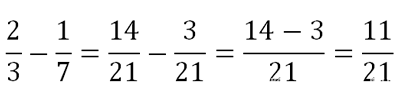
Если работаем со смешанными дробями, приводим к одинаковому знаменателю их дробные части и далее вычитаем как обычно: целую часть из целой, а дробную — из дробной части:
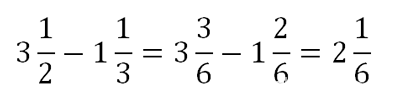
8 Умножение и деление дробей.
Умножать и делить обыкновенные дроби гораздо проще, чем складывать и вычитать, так как не нужно приводить их к одному знаменателю. Запомните простые правила умножения и деления дробей:
Чтобы умножить дробь на натуральное число, нужно числитель умножить на это число, а знаменатель оставить без изменений 
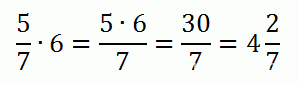
Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель — на знаменатель:
При умножении смешанных дробей нужно сначала записать эти дроби в виде неправильных дробей, а затем умножать как обычно: числитель умножить на числитель, а знаменатель на знаменатель:
Перед тем, как перемножать числа в числителе и знаменателе желательно сократить дробь, то есть избавиться от одинаковых множителей в числителе и знаменателе, как в нашем примере.
Чтобы разделить дробь на натуральное число, нужно знаменатель умножить на это число, а числитель оставить без изменений:
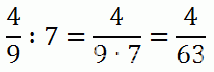
Деление дроби на дробь
Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное делителю (обратную дробь).Что же это за обратная дробь?
Взаимно обратные числа и дроби.
Если мы перевернем дробь, то есть поменяем местами числитель и знаменатель, то получим обратную дробь. Произведение дроби и обратной ей дроби дает единицу. В математике такие числа называют взаимно обратными числами:
Например, числа 
— взаимно обратные, так как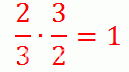 
Таким образом, вернемся к делению дроби на дробь:
Чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю:
При делении смешанных дробей нужно так же, как и при умножении, сначала перевести их в неправильные дроби:
При умножении и делении дробей на целые натуральные числа, можно представлять эти числа так же в виде дробей со знаменателем 1 .
И при делении целого числа на дробь представляем это число в виде дроби со знаменателем 1:
Если у вас не открываются игры или тренажёры, читайте здесь .
Математика. 5 класс
Конспект урока
Понятие дроби
Перечень рассматриваемых вопросов:
- обыкновенная дробь;
- числитель и знаменатель обыкновенной дроби;
- правильная, неправильная дробь.
Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.
Обязательная литература:
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Очень часто в жизни мы слышим такие выражения: «Прошел половину пути», «Купил четвертинку хлеба», «Сделал третью часть от работы». Все эти выражения связаны с новым понятием «дробь». О ней сегодня и пойдёт речь.
Чтобы ввести понятие дроби, выполним следующее задание.
Две части будут весить две третьих килограмма.
Если на отрезке АС укладывается ровно 3 раза отрезок длиной одна пятая сантиметра, то говорят, что длина отрезка равна три пятых сантиметра.
Такие записи называются обыкновенными дробями или просто дробями.
Дробь показывает какую-то часть от целого или единицы. Например, дробь семь восьмых показывает семь восьмых части от единицы.
Обозначенное таким образом число называют рациональным числом. При этом p называется числителем дроби (он всегда находится над чертой), а q – знаменателем дроби (он всегда находится под чертой).
Рассмотрим виды обыкновенных дробей. Обыкновенные дроби можно разделить на следующие виды – правильные, когда числитель меньше знаменателя, и неправильные, когда числитель равен или больше знаменателя.
Сколько часов содержится в четверти суток?
Так как в сутках 24 часа, то нам по условию надо найти четвёртую часть, т. е. разделить двадцать четыре часа на четыре части.
Решим задачу, используя понятие обыкновенной дроби.
В коробке находилось два вида конфет: 5 шоколадных и 6 карамелек. Какую часть всех конфет занимают карамель и шоколад?
Решение: для начала найдём общее количество конфет в коробке, для этого сложим все виды конфет.
5 + 6 = 11 – конфет в коробке.
Теперь можно найти, какую часть от общего количества конфет занимает карамель, а какую шоколадные конфеты. Для этого запишем результат в виде обыкновенной дроби, где в знаменателе укажем общее число конфет. Пять одиннадцатых – часть шоколадных конфет, а шесть одиннадцатых – часть карамели.
Тренировочные задания
№ 1. Сколько минут содержится в одной трети часа?
Решение: для решения этой задачи достаточно вспомнить, что 1 ч = 60 мин.
Найдём третью часть от 60 минут, для этого:
60 мин : 3 = 20 мин
№ 2. Длина отрезка АВ равна 10 см. Чему равен отрезок, длина которого составляет две пятых от длины отрезка АВ?
Решение: сначала найдём, чему равна одна часть из 5 отрезков.
10 см : 5 = 2 см – одна часть.
По условию задачи нужно найти 2 части из пяти, поэтому: 2 см · 2 = 4 см
Обыкновенные дроби
теория по математике числа и вычисления
Обыкновенная дробь – это запись числа в виде:
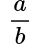
где число a называют числителем, а число b – знаменателем дроби.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.
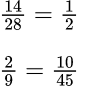Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.
- Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
- Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.
Сокращение дробей
Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.
Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:
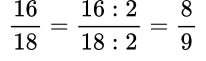
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.
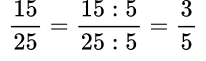Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.
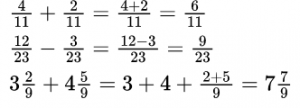
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.
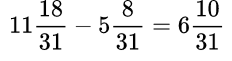
Вычитание обыкновенной дроби из целого числа
Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.
Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).
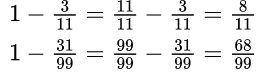Вычитание обыкновенной дроби из бóльшего числа
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.
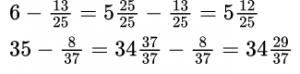
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.
Нахождение общего знаменателя
Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:
2. Затем найти одинаковые множители (подчеркиваем):
В данном случае это только множитель 3.
3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:
12 домножаем на 5: 12×5=60, или
15 домножаем на 2 и 2: 15×2×2=60
Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.
Перемножение знаменателей. Приём №2.
Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.
Пример №8.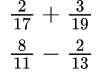 
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.
Последовательный подбор. Приём №3.
Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.
Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.
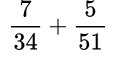
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.
Алгоритм сложения (вычитания)
- Находим общий знаменатель данных дробей.
- Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
- Умножаем каждый числитель на дополнительный множитель.
- Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.
Пример №10.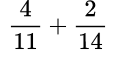
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:
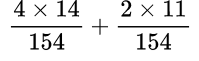Выполняем умножение в числителе: 
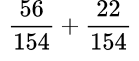Выполняем сложение дробей с одинаковыми знаменателями: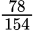 
Умножение обыкновенных дробей
При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).
Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.
Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.
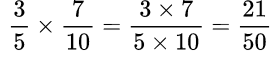
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.
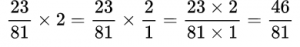
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.
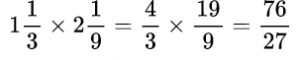
Деление обыкновенных дробей
При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.
Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.
Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.
Пример №14. Делимое умножаем на число, обратное делителю.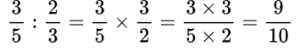 
Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.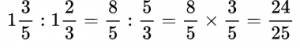 
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.
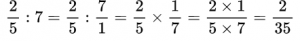
Найдите значение выражения:
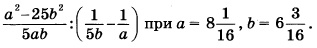
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению: 
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
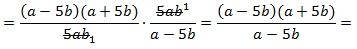сокращаем выражение на (a–5b): 
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): 
Подставим полученные значения в выражение и найдем конечный результат: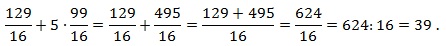 
Ответ: 39
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
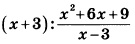
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
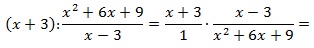
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
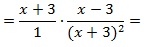
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
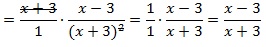
Подставляем числовое значение для х в полученное выражение и находим результат:
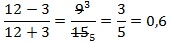Ответ: 0,6
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
при x = √45 , y = 0,5
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
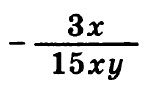
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Подставляем значение a = 13:
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
Суммарно наши действия выглядят так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
pазбирался: Даниил Романович | обсудить разбор | оценить
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
pазбирался: Даниил Романович | обсудить разбор | оценить
Загрузка...