Коллинеарные векторы – условия, признаки и примеры

Коллинеарность векторов, условия коллинеарности векторов.

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).

рис. 1

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = < a_x ; a_y ; a_z > и b = < na_x ; na_y ; na_z >. Найдем их векторное произведение

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

ax	=	ay	.
bx		by

Вектора a и b коллинеарны т.к.	1	=	2	.
	4		8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
	5		9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
	4		8

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	by	=	6	= 2
	ay		3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

ax	=	ay	.
bx		by

3	=	2	.
9		n

Решим это уравнение:

n =	2 · 9	= 6
	3

Ответ: вектора a и b коллинеарны при n = 6.

Примеры задач на коллинеарность векторов в пространстве

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:

ax	=	ay	=	az	.
bx		by		bz

Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12

Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12

Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	by	=	6	= 2
	ay		3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

ax	=	ay	=	az	.
bx		by		bz

3	=	2	=	m
9		n		12

Из этого соотношения получим два уравнения:

3	=	2
9		n

3	=	m
9		12

Решим эти уравнения:

n =	2 · 9	= 6
	3

m =	3 · 12	= 4
	9

Ответ: вектора a и b коллинеарны при n = 6 и m = 4.

Условие коллинеарности векторов

В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.

Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.

Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.

Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.

Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R

Координатная форма условия коллинеарности векторов

Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .

По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.

1. ​​​Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
2. Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z

Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.

Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ – произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Рассмотрим применение условия коллинеарности на конкретных примерах.

Исходные данные: векторы a → = ( 3 – 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.

Решение

Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 – 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 – 2 2 ) = 1 3 2 – 4 + 3 – 2 2 = 1 2 – 1 b y = λ · a y ⇔ 2 + 1 = 1 2 – 1 · 1 ⇔ ( 2 + 1 ) · ( 2 – 1 ) = 1 ⇔ 1 ≡ 1

Т.е. b → = 1 2 – 1 · a → , следовательно, заданные векторы коллинеарны.

Ответ: заданные векторы коллинеарны.

Исходные данные: векторы a → = ( 1 , 0 , – 2 ) и b → = ( – 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.

Решение

Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ – 3 = – 3 · 1 0 = – 3 · 0 6 = – 3 · ( – 2 ) , то верным будет равенство: b → = – 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.

Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 – 2 – 3 0 6 = i → · 0 · 6 + j → · ( – 2 ) · ( – 3 ) + k → · 1 · 0 – k → · 0 · ( – 3 ) – j → · 1 · 6 – i → · ( – 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.

Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.

Решение

Согласно выведенному выше условию, векторы коллинеарны, если

b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7

тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .

Ответ: при p = 6 7 заданные векторы коллинеарны.

Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.

Исходные данные: вектор a → = ( 2 , – 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.

Решение

Ответом может послужить, например, 1 2 · a → = ( 1 , – 3 ) или вектор 3 · a → = ( 6 , – 18 ) .

Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , – 3 ) .

Исходные данные: вектор a → = ( 3 , 4 , – 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.

Решение

Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( – 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , – 1 2 )

Коллинеарная система и примеры

коллинеарные векторы Они являются одним из трех типов существующих векторов. Речь идет о тех векторах, которые находятся в одном направлении или направлении действия. Это означает следующее: два или более векторов будут коллинеарными, если они расположены в виде прямых линий, параллельных друг другу.

Вектор определяется как величина, применяемая к телу, и характеризуется как имеющий направление, смысл и масштаб. Векторы могут быть найдены в плоскости или в пространстве и могут быть разных типов: коллинеарные векторы, параллельные векторы и параллельные векторы.

• 1 колинеальный вектор
• 2 Характеристики
  • 2.1 Пример 1
  • 2.2 Пример 2
  • 2.3 Пример 1
• 3 Коллинеарная векторная система
  • 3.1 Коллинеарные векторы с противоположными значениями
  • 3.2 Коллинеарные векторы с одинаковым смыслом
  • 3.3 Коллинеарные векторы с равными величинами и противоположными значениями
• 4 Разница между коллинеарными и параллельными векторами
• 5 ссылок

Коллинеарные векторы

Векторы коллинеарны, если линия действия одного является точно такой же линией действия всех других векторов, независимо от размера и смысла каждого из векторов..

Векторы используются в качестве представлений в различных областях, таких как математика, физика, алгебра, а также в геометрии, где векторы коллинеарны только тогда, когда их направление одинаково, независимо от того, имеет ли их значение значение.

черты

– Два или более вектора коллинеарны, если соотношение между координатами равно.

Пример 1

У нас есть векторы m = m_x; m_y и n = n_x; n_y. Они коллинеарны, если:

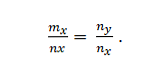
Пример 2

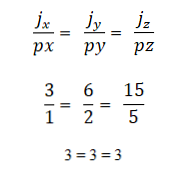
– Два или более векторов коллинеарны, если произведение или вектор умножения равен нулю (0). Это связано с тем, что в системе координат каждый вектор характеризуется своими соответствующими координатами, и если они пропорциональны друг другу, векторы будут коллинеарными. Это выражается следующим образом:

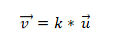
Пример 1

У нас есть векторы a = (10, 5) и b = (6, 3). Чтобы определить, являются ли они коллинеарными, применяется теория детерминантов, которая устанавливает равенство перекрестных произведений. Таким образом, вы должны:

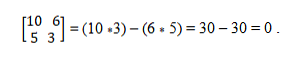
Коллинеарная векторная система

Коллинеарные векторы представлены графически с использованием направления и смысла их, учитывая, что они должны проходить через точку приложения и модуль, который имеет определенный масштаб или длину.

Система коллинеарных векторов формируется, когда два или более векторов воздействуют на объект или тело, представляя силу и действуя в одном направлении..

Например, если к телу приложены две коллинеарные силы, их результат будет зависеть только от направления, в котором они действуют. Есть три случая, которые:

Коллинеарные векторы с противоположными чувствами

Результирующий из двух коллинеарных векторов равен сумме этих:

пример

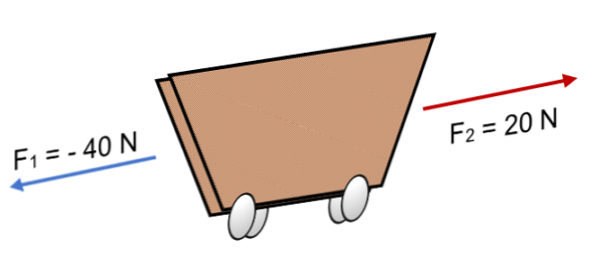
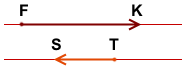
Если на тележку F действуют две силы₁ = 40 Н и F₂ = 20 Н в обратном направлении (как показано на рисунке), результат:

R = Σ F = (- 40 Н) + 20 Н.

Коллинеарные векторы с одинаковым смыслом

Величина результирующей силы будет равна сумме коллинеарных векторов:

пример

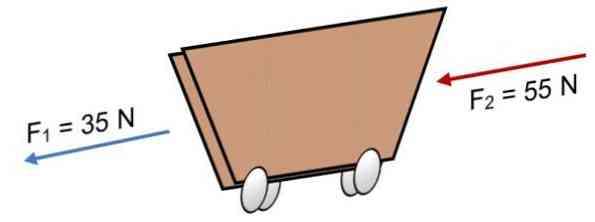
Если на тележку F действуют две силы₁ = 35 Н и F₂ = 55 Н в том же направлении (как показано на рисунке), результат:

R = Σ F = 35 Н + 55 Н.

Положительный результат показывает, что коллинеарные векторы действуют влево.

Коллинеарные векторы с одинаковыми величинами и противоположными значениями

Результирующий из двух коллинеарных векторов будет равен сумме коллинеарных векторов:

Поскольку силы имеют одинаковую величину, но в противоположном направлении, то есть одно будет положительным, а другое отрицательным, при сложении двух сил результирующее значение будет равно нулю.

пример

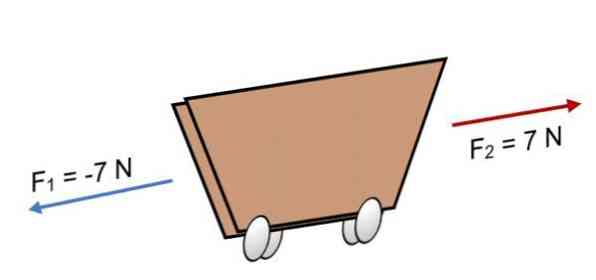
Если на тележку F действуют две силы₁ = -7 N и F₂ = 7 Н, которые имеют ту же величину, но в противоположном направлении (как показано на рисунке), результат:

R = Σ F = (-7 Н) + 7Н.

Поскольку результат равен 0, это означает, что векторы сбалансированы друг с другом и, следовательно, тело находится в равновесии или в состоянии покоя (оно не будет двигаться).

Разница между коллинеарным и параллельным векторами

Коллинеарные векторы характеризуются наличием одинакового направления на одной линии или потому, что они параллельны линии; то есть они являются векторами прямых параллельных линий.

С другой стороны, параллельные векторы определены, потому что они находятся в разных направлениях действия, которые перехвачены в одной точке.

Другими словами, они имеют одну и ту же точку отправления или прибытия – независимо от их модуля, направления или направления – образуя угол между ними.

Системы параллельных векторов решаются математическими методами или графами, которые являются методом параллелограмма сил и методом многоугольника сил. По ним будет определяться значение результирующего вектора, который указывает направление, в котором будет двигаться тело..

По сути, основное различие между коллинеарными векторами и параллельными векторами заключается в линии действия, в которой они действуют: коллинеарные действуют в одной линии, тогда как параллельные в разных.

То есть коллинеарные векторы действуют в одной плоскости: «X» или «Y»; и одновременный акт в обеих плоскостях, начиная с одной и той же точки.

Коллинеарные векторы не находятся в одной точке, как параллельные, потому что они параллельны друг другу.

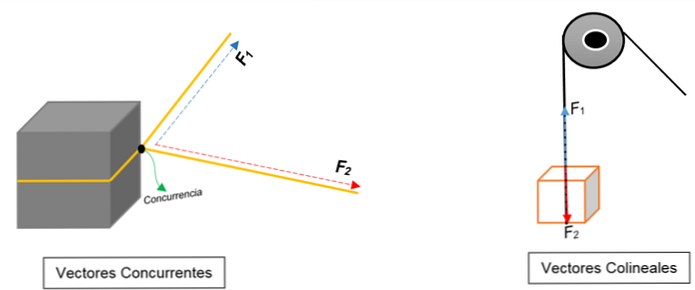
На левом изображении вы можете увидеть блок. Он связан веревкой, а узел делит его на две части; когда тянуть в разные стороны и с разными силами, блок будет двигаться в том же направлении.

Представлены два вектора, которые совпадают в точке (блоке), независимо от их модуля, смысла или направления.

Вместо этого на правом изображении появляется шкив, который поднимает коробку. Веревка представляет собой линию действий; когда его тянут, на него действуют две силы (векторы): одна сила натяжения (при подъеме на блок) и другая сила, та, которая воздействует на вес блока. Оба имеют одинаковое направление, но в противоположных направлениях; не соглашайтесь в точке.

Коллинеарные векторы

Какие векторы называются коллинеарными?

Какими свойствами обладают коллинеарные векторы?

Векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.

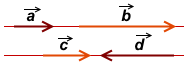Например, все векторы

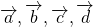
коллинеарны между собой.

Нулевой вектор считают коллинеарным любому вектору.

Коллинеарные векторы делятся на сонаправленные и противоположно направленные.

Векторы

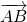
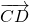
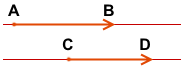
называются сонаправленными (или одинаково направленными), если лучи AB и CD сонаправлены.

(Сонаправленность векторов записывают с помощью знака ↑↑).

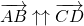
Векторы

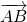
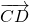
называются противоположно направленными, если лучи AB и CD противоположно направлены.

(Противоположное направление векторов обозначают знаком ↑↓).

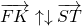
(Свойство коллинеарных векторов)

У коллинеарных векторов соответствующие координаты пропорциональны

То есть если векторы

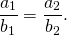
(Признак коллинеарных векторов)

Если соответствующие координаты векторов пропорциональны, то эти векторы коллинеарны.

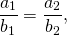
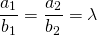
при λ>0 векторы сонаправлены

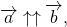
при λ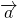

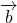
неколлинеарны, то любой вектор

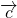
можно разложить как

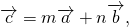
где m и n — некоторые числа.

Такое разложение единственно.

Векторы: третий уровень сложности

Знакомимся с коллинеарностью.

Для большинства людей искусственный интеллект — это нечто сложное и таинственное. А для математиков это синоним фразы «перемножение матриц». С точки зрения человека, который владеет линейной алгеброй, в искусственном интеллекте нет ничего загадочного.

Мы хотим, чтобы вы тоже смогли понять искусственный интеллект на уровне математики. Для этого у нас идёт цикл статей про линейную алгебру:

• Что это такое
• Базовые операции с векторами
• И вот теперь — коллинеарность

Сама тема несложная, но конкретно этот шаг вам ничего не даст в практическом смысле. Но если вам хватит терпения, на базе этих знаний мы уже перейдём к матрицам.

Что за коллинеарность

Представьте два вектора, которые находятся в одной плоскости и располагаются параллельно друг другу. При этом у них может быть разная длина. Такое расположение делает связку векторов коллинеарными, или, по-простому, линейно зависимыми.

И наоборот: если вектора находятся в одной плоскости и располагаются не параллельно друг относительно друга, то их считают линейно независимыми — неколлинеарными. Пока что ничего сложного.

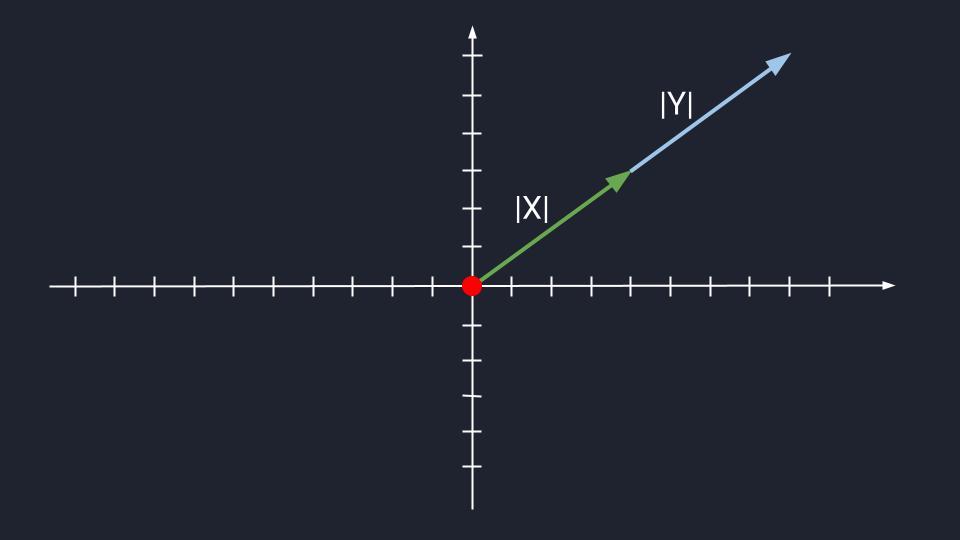Коллинеарные векторы 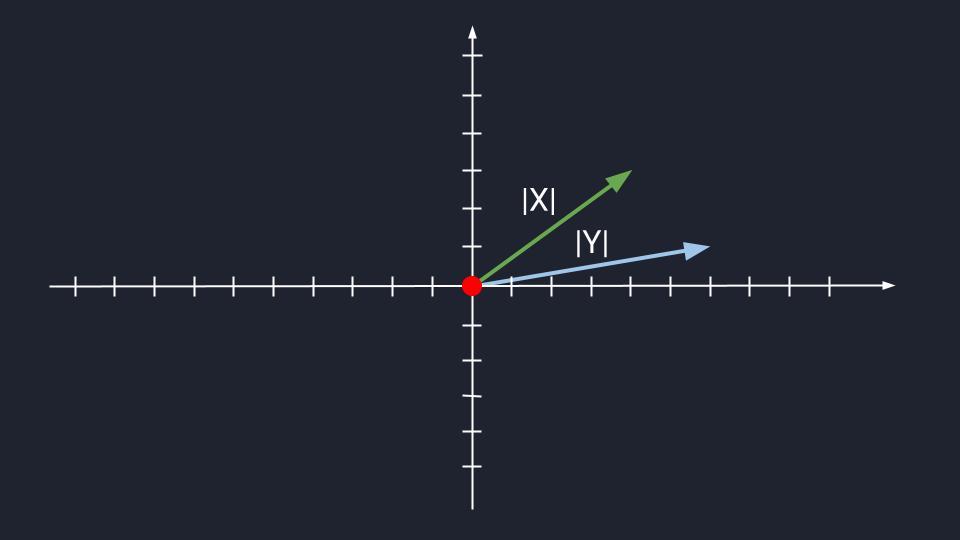Неколлинеарные векторы

Сложение коллинеарных и неколлинеарных векторов

Очевидно, что сложить два коллинеарных вектора очень легко: откладываем второй вектор от начала первого, получится новый вектор. Он будет коллинеарным своим слагаемым, они все будут лежать, грубо говоря, на одной линии.

Можно представить, что вы идёте прямо: каждый ваш шаг — это вектор. Каждый новый шаг — новый вектор. Но если все их сложить, получится один большой прямой вектор длиной как все ваши шаги.

Теперь попробуем сложить пару неколлинеарных векторов. Это как если бы мы сначала сделали шаг немного правее, а потом сделали бы шаг влево. Шага два, но если соединить начало и конец пути, он не будет совпадать с траекториями наших шагов. Появится какой-то новый вектор, с новым направлением, и он будет неколлинеарным по отношению к своим слагаемым.

Также пару неколлинеарных векторов из одной плоскости можно растянуть и развернуть в пространстве. Если их сложить, также появится новый вектор.

У математиков такой вектор называют базисом. Когда базис находится на плоскости или в пространстве, то он может единственным образом превращаться обратно в пару неколлинеарных векторов, которые его сформировали.

Правило работает, когда мы масштабируем и меняем расположение векторов в пространстве. Если мы изменим направление исходных векторов, то получим новый базис.

Базис — понятие из высшей математики, поэтому, если сейчас сложно, не отчаивайтесь. Студенты-математики когда-то тоже отчаивались.

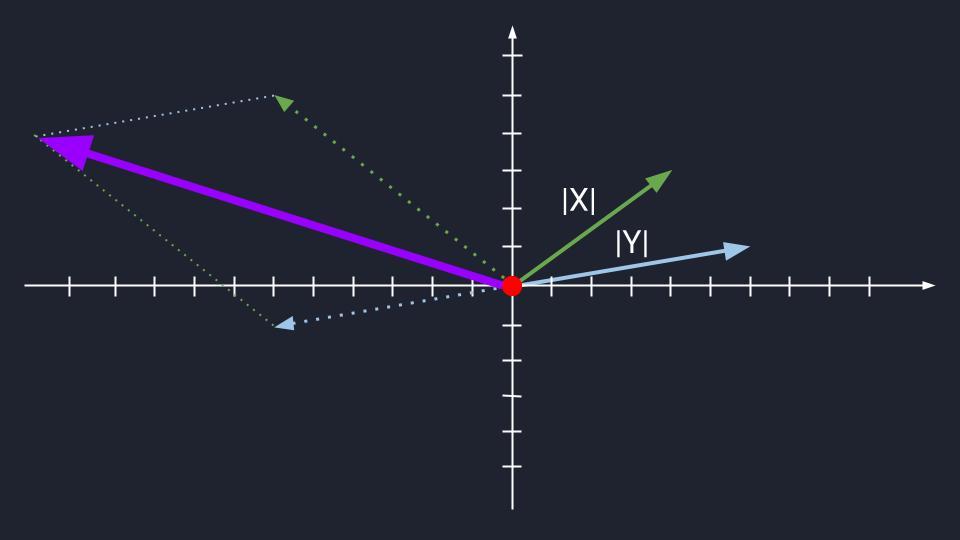Мы изменили пару неколлинеарных векторов и сформировали из них базис — получили новый фиолетовый вектор с собственной системой координат 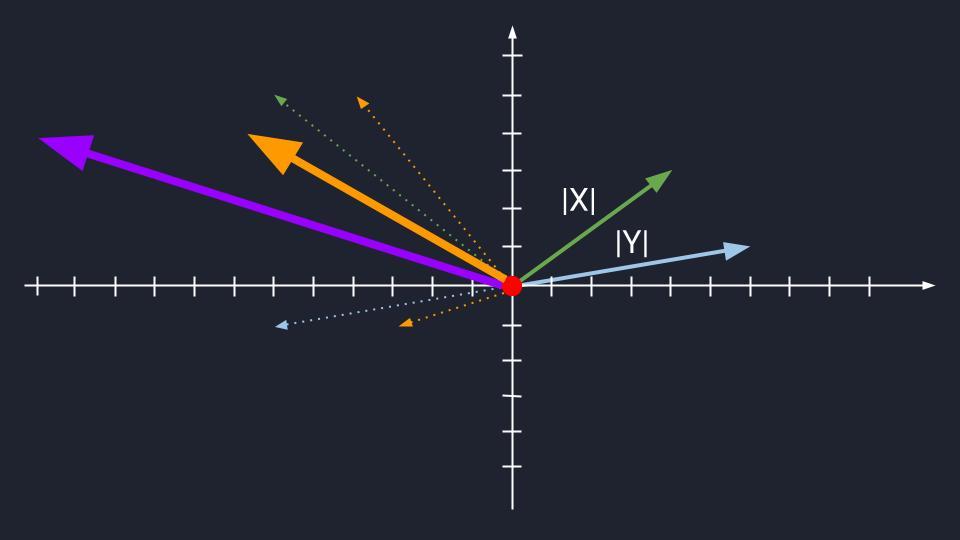Теперь мы изменили исходные неколлинеарные векторы и получили новый базис — это оранжевый вектор

Как определять неколлинеарность

Когда мы работаем с короткими векторами, всё очевидно: нарисовали систему координат, отложили на ней векторы, они либо совпали, либо не совпали. Если совпали — коллинеарные, если нет — неколлинеарные.

А теперь представьте, что вектора настолько огромные, что мы физически не можем их нарисовать и сопоставить. Например,

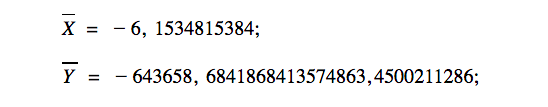
Как такое нарисовать? Как проверить коллинеарность? Вот тут начинается магия алгебры.

Есть три способа проверки линейной зависимости векторов. Для простоты вычислений проверим эти три способа на вот этих всё ещё простых векторах:

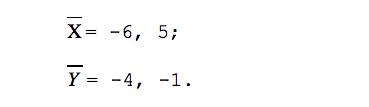
По этим координатам ответим на два вопроса: являются ли предложенные вектора линейно зависимыми (то есть коллинеарными) и можно ли их раскладывать по базису.

Первый способ. Запишем простую систему уравнений: возьмём первую координату каждого вектора и приравняем её ко второй координате каждого вектора, умноженной на неизвестное число λ. Вычислим λ и сравним результаты.

Знак λ здесь по традиции и для удобства. На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».

Составляем систему уравнений:

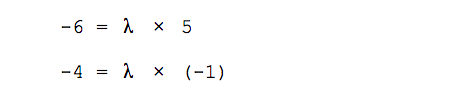
Вычисляем значение λ:

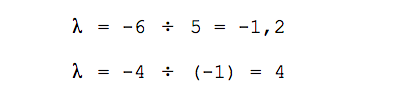
Сравниваем результат и делаем вывод:

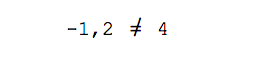
Мы получили разное значение для неизвестного числа λ и поэтому наши векторы будут считаться линейно независимыми. Из них можно получить базис.

Если бы значение λ совпало, то мы бы имели дело с линейно зависимыми векторами.

Второй способ. Проверяем координаты векторов на пропорциональность: берём первую координату первого вектора, делим её на первую координату второго вектора. Повторяем это же действие со вторыми координатами: берём вторую координату первого вектора и делим её на вторую координату второго вектора.

Получаем такую пропорцию:

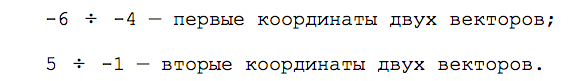
Считаем значение и сравниваем результат:

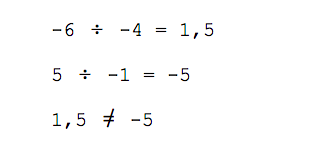
Равенство не выполняется, и поэтому между векторами нет зависимости.

Третий способ. Используем четыре элемента наших координат для поиска определителя — скалярной величины, с которой мы подробно познакомимся в следующих статьях во время решения матричных уравнений. Сейчас нам не нужны подробности, и для проверки линейной зависимости достаточно формулы.

Записываем в две строки координаты наших векторов:

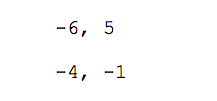
Переводим координаты векторов в определитель — добавляем с двух сторон вертикальную черту и получаем простую квадратную матрицу размером 2 на 2:

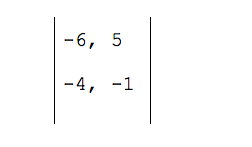
В полученной матрице две диагонали. Числа −6 и −1 образуют главную диагональ; числа −4 и 5 — вторую диагональ. Чтобы найти определитель, нам нужно умножить числа главной и второй диагонали, а затем вычесть их разницу.

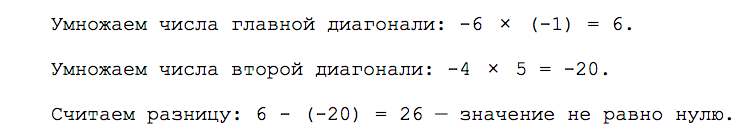
Если из координат вектора мы получили определитель и он не равен нулю, то векторы считаются линейно независимыми и подходят для разложения по базису.

И наоборот: нулевой определитель указывает на линейную зависимость векторов.

Что из этого нужно запомнить

• С точки зрения векторов важно, они сонаправленные или нет. По-другому — они коллинеарны или нет.
• Коллинеарность влияет на то, что можно делать с этими векторами. Например, неколлинеарные векторы можно разложить по базису.
• Базис — это вектор, который можно разложить на те самые неколлинеарные векторы.
• Коллинеарность легко проверяется через уравнения. Строить векторы на координатной плоскости необязательно.

Что дальше

Следующий шаг — матрицы. Это те самые, которые лежат в основе всех нейронок и искусственного интеллекта. Матрица — это таблица чисел, с которыми можно проводить различные вычисления.

Коллинеарные векторы: система и примеры

Содержание:

• Коллинеарные векторы
• характеристики
• Пример 1
• Пример 2
• Пример 1
• Коллинеарная векторная система
• Коллинеарные векторы с противоположными направлениями
• пример
• Коллинеарные векторы с одинаковым смыслом
• пример
• Коллинеарные векторы с равными величинами и противоположными направлениями
• пример
• Разница между коллинеарными и параллельными векторами
• Ссылки

В коллинеарные векторы они являются одним из трех типов существующих векторов. Это те векторы, которые находятся в одном направлении или линии действия. Это означает следующее: два или более вектора будут коллинеарными, если они расположены на линиях, параллельных друг другу.

Вектор определяется как величина, приложенная к телу, и характеризуется направлением, смыслом и масштабом. Векторы могут находиться на плоскости или в пространстве и могут быть разных типов: коллинеарные векторы, параллельные векторы и параллельные векторы.

Коллинеарные векторы

Векторы коллинеарны, если линия действия одного в точности совпадает с линией действия всех других векторов, независимо от размера и направления каждого из векторов.

Векторы используются в качестве представлений в различных областях, таких как математика, физика, алгебра, а также в геометрии, где векторы коллинеарны только тогда, когда их направление одинаково, независимо от того, является ли их смысл другим.

характеристики

– Два или более вектора коллинеарны, если соотношение между координатами одинаковое.

Пример 1

У нас есть векторы m = и n = . Они коллинеарны, если:

Пример 2

– Два или более вектора коллинеарны, если векторное произведение или умножение равно нулю (0). Это связано с тем, что в системе координат каждый вектор характеризуется соответствующими координатами, и если они пропорциональны друг другу, векторы будут коллинеарными. Это выражается следующим образом:

Пример 1

Имеем векторы a = (10, 5) и b = (6, 3). Чтобы определить, являются ли они коллинеарными, применяется теория детерминантов, которая устанавливает равенство перекрестных произведений. Таким образом, вам необходимо:

Коллинеарная векторная система

Коллинеарные векторы графически представлены с использованием их направления и направления – с учетом того, что они должны проходить через точку приложения – и модуля, который имеет определенный масштаб или длину.

Система коллинеарных векторов образуется, когда два или более вектора действуют на объект или тело, представляя силу и действуя в одном направлении.

Например, если к телу приложены две коллинеарные силы, их результирующая будет зависеть только от направления, в котором они действуют. Есть три случая, а именно:

Коллинеарные векторы с противоположными направлениями

Результирующая двух коллинеарных векторов равна их сумме:

пример

Если на тележку действуют две силы F₁ = 40 N и F₂ = 20 Н в обратном направлении (как показано на рисунке), результат:

R = ∑ F = (- 40 Н) + 20 Н.

Коллинеарные векторы с одинаковым смыслом

Величина результирующей силы будет равна сумме коллинеарных векторов:

пример

Если на тележку действуют две силы F₁ = 35 N и F₂ = 55 N в том же направлении (как показано на изображении), результат:

R = ∑ F = 35 N + 55N.

Положительный результат указывает на то, что коллинеарные векторы действуют слева.

Коллинеарные векторы с равными величинами и противоположными направлениями

Результат двух коллинеарных векторов будет равен сумме коллинеарных векторов:

Поскольку силы имеют одинаковую величину, но в противоположном направлении, то есть одна будет положительной, а другая отрицательной, при сложении двух сил результирующая будет равна нулю.

пример

Если на тележку действуют две силы F₁ = -7 N и F₂ = 7 Н, которые имеют ту же величину, но в противоположном направлении (как показано на изображении), результат:

R = ∑ F = (-7 Н) + 7 Н.

Поскольку результат равен 0, это означает, что векторы уравновешивают друг друга и, следовательно, тело находится в равновесии или в состоянии покоя (оно не будет двигаться).

Разница между коллинеарными и параллельными векторами

Коллинеарные векторы характеризуются тем, что они имеют одинаковое направление на одной и той же линии или потому, что они параллельны прямой; то есть они являются направляющими векторами параллельных линий.

Со своей стороны, параллельные векторы определены, потому что они находятся в разных направлениях действия, которые пересекаются в одной точке.

Другими словами, они имеют одну и ту же точку происхождения или прибытия – независимо от их модуля, направления или направления – образующие между ними угол.

Параллельные векторные системы решаются математическими или графическими методами, которые представляют собой метод параллелограмма сил и метод многоугольника сил. Через них будет определено значение результирующего вектора, который указывает направление, в котором будет двигаться тело.

По сути, основное различие между коллинеарными и параллельными векторами – это линия действия, в которой они действуют: коллинеарные векторы действуют на одной линии, а параллельные – на разных линиях.

То есть коллинеарные векторы действуют в одной плоскости, «X» или «Y»; а параллельные действуют в обеих плоскостях, начиная с одной и той же точки.

Коллинеарные векторы не пересекаются в одной точке, в отличие от параллельных векторов, поскольку они параллельны друг другу.

На левом изображении вы можете увидеть блок. Он связан веревкой, а узел делит его пополам; Если тянуть в разные стороны и с разными усилиями, блок будет двигаться в одном направлении.

Представлены два вектора, которые совпадают в точке (блоке), независимо от их модуля, направления или направления.

Вместо этого на правом изображении есть шкив, который поднимает коробку. Веревка представляет собой линию действия; когда его тянут, на него действуют две силы (вектора): сила натяжения (при подъеме блока) и другая сила, которая оказывает влияние на вес блока. Оба имеют одинаковое направление, но в противоположных направлениях; они не согласны в одном пункте.

Ссылки

1. Эсталелья, Дж. Дж. (1988). Векторный анализ. Том 1.
2. Гупта, А. (s.f.). Тата Макгроу-Хилл Образование.
3. Джин Хо Квак, С. Х. (2015). Линейная алгебра. Springer Science & Business Media.
4. Монтьель, Х. П. (2000). Физика 1 для технологического бакалавриата. Grupo Editor Patria.
5. Сантьяго Бурбано де Эрсилья, К. Г. (2003). Общая физика. Редакция Тебар.
6. Синха, К. (s.f.). Учебник математики XII Том 2. Публикации Растоги.

ДМТ (наркотик): действие и механизм действия этого токсичного вещества

Простые машины: история, характеристики, виды, примеры

Как найти вектор, коллинеарный вектору

Вы будете перенаправлены на Автор24

Понятие коллинеарности векторов

Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Обозначение: $overline$ – вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline$ (рис. 1).

Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Далее рассмотрим, какие векторы называются коллинеарными.

Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).

Готовые работы на аналогичную тему

Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ

Также введем определение векторного произведения, которое будет нам необходимо далее.

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.

Чтобы найти векторное произведение, будем пользоваться формулой

$overline<α>хoverline<β>=beginoverline&overline&overline\α_1&α_2&α_3\β_1&β_2&β_3end$

Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам

Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.

Доказательство.

Необходимость: Пусть нам даны векторы $overline<α>$ и $overline<β>$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Так как векторы $overline<α>$ и $overline<β>$ коллинеарны, то они будут либо сонаправленными, либо противоположно направленными. Без ограничения общности, будем считать, что они будут сонаправлены, то есть $overline<α>↑↑overline<β>$. Умножим один из этих векторов на действительное, большее нуля, число $r$, так, чтобы длины векторов $roverline<α>$ и $overline<β>$ были равны между собой. По определению умножения векторов на число, получим, что $roverline<α>↑↑overline<β>$. Но тогда, по определению равенства векторов, получим, что $roverline<α>=overline<β>$. Из этого равенства получим, что

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $overline<α>$ и $overline<β>$ будут коллинеарными.

Из данных равенств следует, что $roverline<α>=overline<β>$.

Имеются два случая:

В этом случае, по определению умножения вектора на число, получим, что $roverline<α>↑↓overline<β>$.

В этом случае получим, что $roverline<α>↑↑overline<β>$.

Тогда, в обоих случаях получаем доказательство коллинеарности векторов $overline<α>$ и $overline<β>$.

Ответ: теорема доказана.

Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.

Доказательство.

Разложим второй вектор:

Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.

Признаки и свойства коллинеарности векторов через их произведение

Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.

Доказательство.

Необходимость: Пусть нам даны векторы $overline<α>$ и $overline<β>$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать, что $overline<α>хoverline<β>=overline<0>$.

Так как векторы коллинеарны, то, по теореме 1, верны равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Найдем $overline<α>хoverline<β>$ по формуле

$overline<α>хoverline<β>=beginoverline&overline&overline\α_1&α_2&α_3\β_1&β_2&β_3end=beginoverline&overline&overline\rβ_1&rβ_2&rβ_3\β_1&β_2&β_3end=rbeginoverline&overline&overline\β_1&β_2&β_3\β_1&β_2&β_3end=rcdot overline<0>=overline<0>$

Достаточность: Пусть верно равенство $overline<α>хoverline<β>=overline<0>$, докажем, что векторы $overline<α>$ и $overline<β>$ коллинеарны. Так как векторное произведение равняется $overline<0>$, то его длина также равняется нулю. Следовательно, угол между $overline<α>$ и $overline<β>$ равняется $180^circ$ или $0^circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.