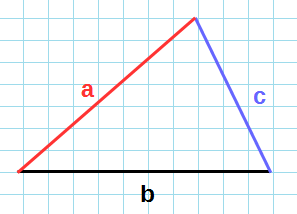
Теорема косинусов и синусов

О чем эта статья:
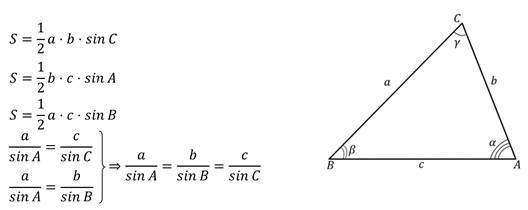
Формулировка и доказательство теоремы косинусов
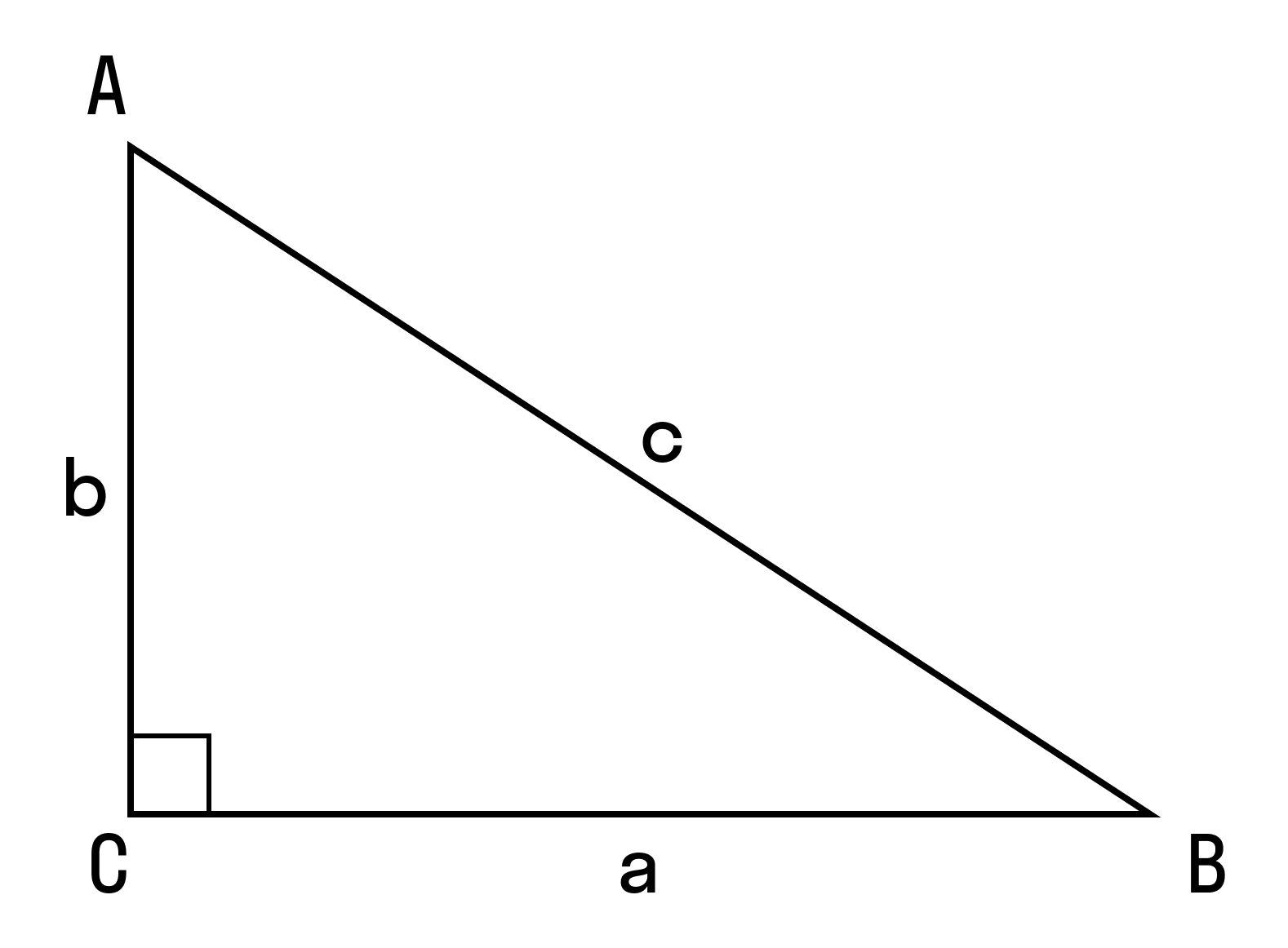
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Из формулы следует: a 2 = c 2 – b 2
К полученному выражению прибавим и отнимем квадрат второго катета:
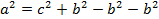
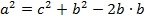
Но так как b = c * cos α, то
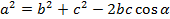
Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.
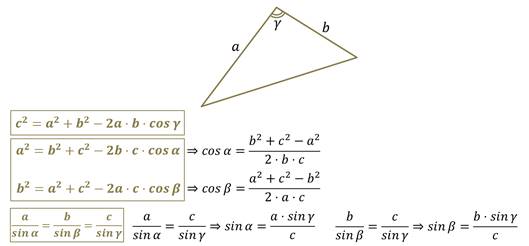
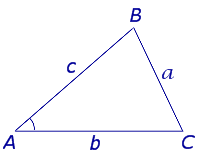
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 – 2bc cos α
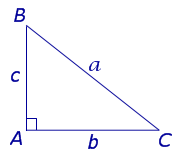
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC 2 = a 2 = (b cos α – c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α – 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) – 2bc cos α + c 2
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
b 2 (cos 2 α + sin 2 α) – 2bc cos α + c 2 = b 2 + c 2 – 2bc cos α
Что и требовалось доказать.
Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:

- Когда b 2 + c 2 – a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 – a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 – a 2
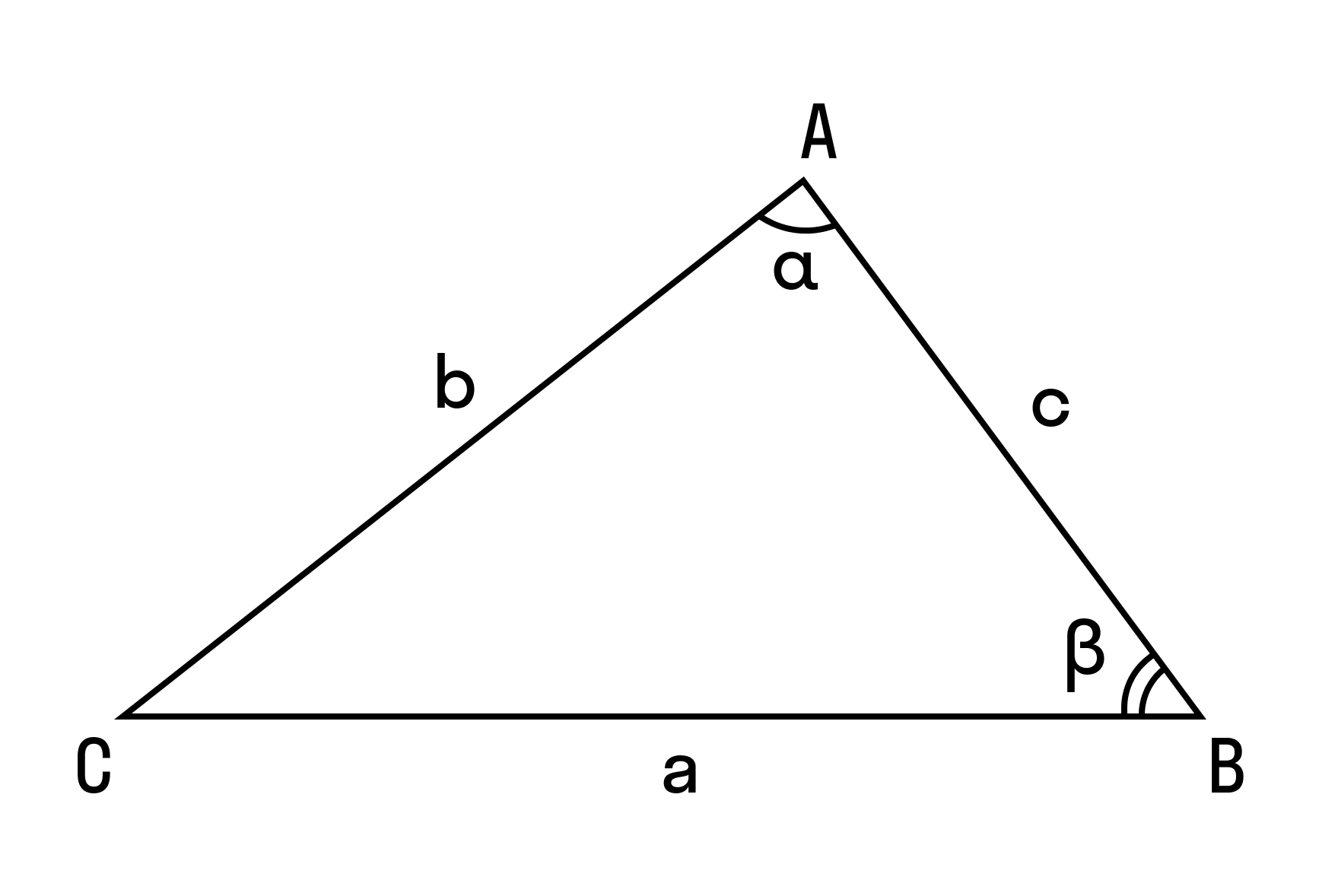
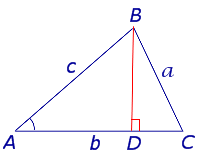
Сформулируем еще одно доказательство теоремы косинусов.
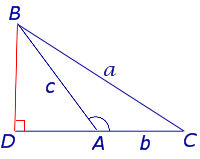
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b * cos α,
- DB = c – b * cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 – (b * cos α) 2
- h 2 = a 2 – (c – b * cos α) 2
Приравниваем правые части уравнений:
- b 2 – (b * cos α) 2 = a 2 – (c – b * cos α) 2
- a 2 = b 2 + c 2 – 2bc * cos α
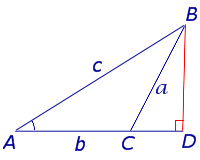
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 – 2ac * cos β;
- c 2 = a 2 + b 2 – 2ab * cos γ.
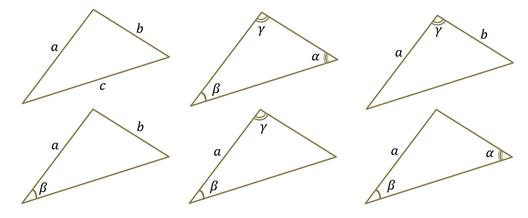
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 – 2bc cos α
b 2 = c 2 + a 2 – 2ca cos β
c 2 = a 2 + b 2 – 2ab cos γ

Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.
Описание формулы косинуса угла из теоремы косинусов
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:





Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
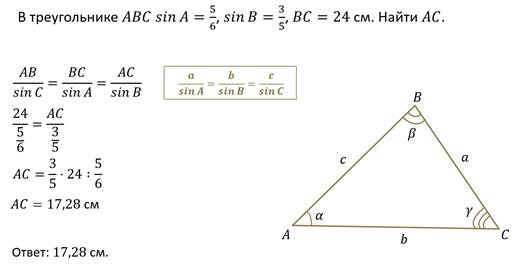
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
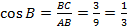
Из треугольника СМВ по теореме косинусов найдём СМ: 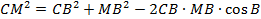

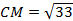
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
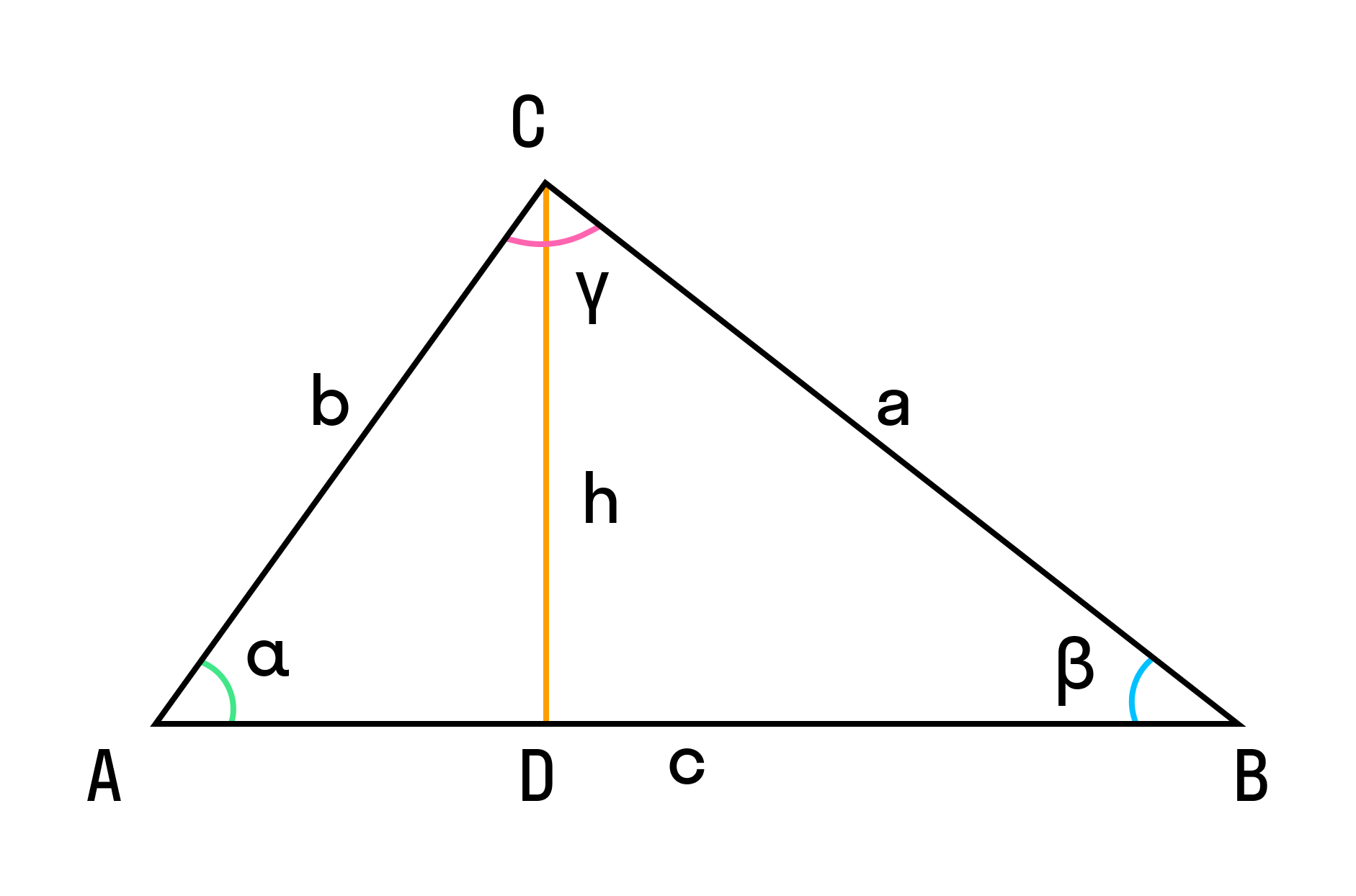
Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение: Полезные формулы теоремы косинусов: Как видно из указанного выше, с помощью теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов. Теорема Пифагора . В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы . Доказательство . Докажем, что длины сторон произвольного прямоугольного треугольника ABC (рис.1) С этой целью рассмотрим квадрат квадрат со стороной, равной c , изображённый на рисунке 2. Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC (рис.3, рис.4), и площади квадрата со стороной, равной a – b (рис.5). Поэтому справедливо равенство что и требовалось доказать. Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами Тогда имеет теорема косинусов для этого треугольника может быть записана в виде: На рисунке для удобства дальнейших рассуждений угол С обозначен углом Понятно, что если бы вы выражали другую сторону треугольника, например, сторону Пусть есть треугольник ABC. Из вершины C на сторону AB опустили высоту CD. Значит: Записываем теорему Пифагора для 2-х прямоугольных треугольников ADC и BDC: h 2 = b 2 – (b cos α) 2 (1) h 2 = a 2 – (c – b cos α) 2 (2) Приравниваем правые части уравнений (1) и (2): b 2 – (b cos α) 2 = a 2 – (c – b cos α) 2 a 2 = b 2 + c 2 – 2bc cos α. Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше. Определить стороны b и c: b 2 = a 2 + c 2 – 2ac cos β c 2 = a 2 + b 2 – 2ab cos γ. В плоском треугольнике квадрат стороны равняется сумме квадратов двух других сторон минус удвоенное произведение данных сторон, умноженное на косинус угла между ними. a 2 = b 2 + c 2 – 2bc cos α Если угол острый, то справедлива формула: a 2 = b 2 + c 2 −2bx Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей. Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне всё же пересиливает. Тем более, что доказательство в результате получается удивительно простым и запоминающимся. Сейчас вы в этом убедитесь. Заменим стороны нашего треугольника следующими векторами: Теперь возьмём скалярный квадрат обеих частей полученного выражения. В результате чего получим: Я напоминаю, что по определению скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Из этого определения также следует, что скалярный квадрат вектора равен квадрату его длины. Действительно, ведь угол между вектором и им же самим равен нулю, то есть соответствующих косинус равен 1. То есть остаётся только квадрат длины вектора. Исходя из этого мы сразу получаем выражение для теоремы косинусов: Что и требовалось доказать. Причём данное доказательство хорошо ещё тем, что позволяет лучше запомнить саму формулу. Ведь теперь становится понятным, откуда берётся этот хвост Кстати, в случае, когда угол Теорема косинусов . Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними. Доказательство . Рассмотрим сначала треугольник ABC , у которого углы A и С – острые (рис.6). Докажем, что длины сторон этого треугольника удовлетворяют равенству С этой целью проведём высоту BD из вершины B (рис.7). В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства BD = c sin A, AD = c cos A, DC = b – AD = b – c cos A. Из теоремы Пифагора , применённой к прямоугольному треугольнику BDC , получим Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана. Замечание 1 . Для того, чтобы получить полное доказательство теоремы косинусов, необходимо рассмотреть также и следующие случаи:
Угол A – прямой (рис. 9).
Угол A – тупой (рис.10). Во всех перечисленных случаях доказательства теоремы косинусов проводятся совершенно аналогично тому, как это было сделано для случая острых углов A и C , и мы рекомендуем читателю провести эти доказательства в качестве полезного и несложного упражнения. Замечание 2 . В случае, когда угол A является прямым углом, формула (1) принимает вид откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов. Замечание 3 . Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например, Задание 1 Решение: Задание 2 Решение: Следовательно, угол α = arccos (-1/6) ≈ 99,59°. Теорема косинусов для прямоугольного треугольника. Рассмотрим прямоугольный треугольник ABC: По теореме косинусов сторона «а» равна: но угол А прямой, косинус прямого угла равен нулю, отсюда получаем: Таким образом мы получили формулу теоремы Пифагора: Треугольник является самой простой фигурой на плоскости, которая подробно рассматривается в классах общеобразовательных школ на уроках геометрии. Знание ее характеристик важно для понимания методов решения многих практических задач. Формулы для треугольника и теорема косинусов в частности являются математическим инструментом, позволяющим вычислять любые свойства фигуры. Прежде чем рассматривать теорему косинусов для треугольника и формулу, которая математически ее выражает, следует познакомиться с самим геометрическим объектом подробнее. Треугольник представляет собой плоскую фигуру, которая состоит из двух типов элементов: Если две стороны треугольника равны между собой и отличаются от третьей, его называют равнобедренным. Если все имеют одинаковую длину, речь идет о равностороннем объекте. Важным свойством любого треугольника является равенство суммы его трех углов 180°. Этот факт справедлив для всех типов фигуры на плоскости. Для описания характеристик объекта в геометрии используют специальные линии. Основными из них являются: Для равносторонней фигуры все 3 типа линий совпадают друг с другом, для равнобедренного треугольника только для угла, образованного равными сторонами, они являются одинаковыми. О треугольнике человечеству известно все, поскольку это самая простая геометрическая фигура. Кроме того, до настоящего времени дошли некоторые работы греческих мыслителей и даже древних египтян, которые были посвящены рассмотрению ее свойств. В общем случае можно назвать 3 основные теоремы, которые в полной мере описывают главные характеристики треугольника. К ним относятся: Эти 3 теоремы и соответствующие им математические выражения являются независимыми и применяются для решения многих практических проблем. Она также звучит как закон косинусов для треугольника и представляет собой обобщение теоремы Пифагора на фигуру произвольного типа. Ее формулировка связывает 3 стороны и угол в единое равенство. Закон косинусов заключается в следующем: квадрат произвольной стороны треугольника равен сумме квадратов двух оставшихся его сторон за вычетом удвоенного произведения их длин, которые умножены на косинус угла между ними. Чтобы записать соответствующее математическое выражение, следует ввести некоторые обозначения. Пусть в фигуре ABC сторона, которая лежит напротив угла C, то есть AB = c, по аналогии, BC = a и AC=b. Углы при вершинах A, B и C удобно обозначать малыми греческими буквами α, β и γ, соответственно. Тогда формула теоремы косинусов запишется в следующем математическом виде: c 2 = a 2 + b 2 — 2*a*b*cos (γ). Зная 3 любых элемента фигуры, можно вычислить все остальные ее характеристики. При этом хотя бы одна из известных величин должна быть линейным параметром. Это утверждение доказать несложно, если представить 2 подобных треугольника, которые имеют попарно равные углы, но разную длину сторон (одна фигура является миниатюрной копией другой). Иными словами, знание трех углов не является достаточным условием для определения свойств треугольника. Практически во всех языках мира теорема носит название закона косинусов и не имеет конкретного автора. Однако, во французском языке она носит имя персидского математика Аль-Каши, жившего в конце XIV — начале XV веков. Согласно историческому анализу, именно с теориями этого философа связана современная формулировка теоремы. Взаимоотношением между сторонами треугольника человечество интересовалось с давних времен. В труде греческого философа Евклида, который называется «Элементы» и датируется III веком до н. э., появляется впервые некое подобие рассматриваемого закона. Однако Евклиду не были известны тригонометрические функции, поэтому в своем труде он отдельно рассматривал тупоугольные и остроугольные фигуры и приводил для их сторон соответствующие равенства через известные длины, например, высоту. В начале X века, когда в мире правили Средние века, арабский математик и астроном Аль-Баттани использовал работы Евклида для сферической геометрии. Его достижения сделали возможным проведения некоторых космических расчетов, например, вычисление расстояния от Земли до Солнца. Первые таблицы тригонометрических функций синуса и косинуса появились приблизительно в XV веке. Эти достижения в математике позволили Аль-Каши, математику из школы Самарканда, переформулировать закон косинусов в удобном для использования виде. Впоследствии француз Франсуа Виет независимо от Аль-Каши получил то же самое математическое выражение для сторон треугольника с использованием тригонометрических функций. Начиная с конца XVII столетия, когда швейцарец Леонард Эйлер ввел в математику новую нотацию, теорема Аль-Каши приобрела современную форму. Кратко следует отметить, что существуют несколько способов доказательства теоремы. Среди них можно перечислить следующие: Последний способ доказательства теоремы косинусов является самым простым и носит общий характер. Его может реализовать каждый школьник, который умеет вычитать вектора друг из друга и знает, как рассчитывается их скалярное произведение. Закон косинусов служит для определения неизвестных длин сторон либо углов в треугольнике. Однако общая математическая формулировка имеет ряд частных случаев в зависимости от типа фигуры, к которой ее применяют. Для равнобедренного треугольника, у которого стороны a и b равны, нахождение c сведется к вычислению следующего равенства: В случае равностороннего треугольника все стороны равны a = b = c. Все углы также являются одинаковыми и соответствуют 60°(180°/3). Для такой фигуры нет смысла в использовании теоремы, поскольку в ней всегда существует лишь одна неизвестная — сторона a. Прямоугольный треугольник по отношению к теореме косинусов является специальным случаем. Благодаря этой фигуре появились понятия синуса, косинуса, тангенса и котангенса как функций, отражающих взаимоотношения между катетами и гипотенузой. Каждый школьник знает, что возведенная длина гипотенузы в квадрат эквивалентна сумме квадратов длин двух других сторон, называемых катетами. Однако, мало кто понимает, что это математическое равенство является не чем иным, как частным случаем закона косинусов. Показать это несложно, если записать изучаемую теорему для гипотенузы c. Тогда получается следующее равенство: c 2 = a 2 + b 2 — 2*a*b*cos (90 °). Если обратится к таблице тригонометрических функций, в ней видно, что косинус прямого угла равен нулю. В результате вычитаемое в правой части равенства обращается в ноль, и равенство сводится к типичной теореме Пифагора. Известно, что стороны треугольника равны 6 см, 8 см и 10 см. Необходимо найти площадь этой фигуры. Для решения задачи можно воспользоваться ресурсами интернета, которые предлагают множество сайтов, где с использованием онлайн-калькуляторов можно по известным данным найти нужную величину. Тем не менее представляет интерес решить эту задачу с использованием теоремы косинусов. Площадь любого треугольника может быть вычислена так: Здесь h — высота, проведенная к a. Известные стороны a = 6 см, b = 8 см, c = 10 см. Чтобы найти высоту h следует сначала рассчитать угол между a и c. Для этого можно применить закон косинусов: β = arccos ((a 2 + c 2 — b 2 )/(2*a*c)) = arccos ((6 2 + 10 2 — 8 2 )/(2*6*10)) = 53,13 °. Теперь, если рассмотреть треугольник, образованный высотой h, стороной c и частью стороны a, можно увидеть, что он является прямоугольным (c — гипотенуза). В нем h может быть найдена через синус угла β: h = c*sin (β) = 10* sin (53,13 °) = 8 см. Длина высоты h равна таковой для стороны b. Это означает, что исходный треугольник являлся прямоугольным (можно проверить через теорему Пифагора). Его площадь составляет: S = ½*a*h = ½*a*b = ½*6*8 = 24 см 2 . Таким образом, теорема косинусов является универсальным инструментом для решения геометрических задач с треугольниками. С помощью нее по трем известным параметрам можно найти все остальные характеристики фигуры, включая ее площадь. Что же такое теорема косинусов? Представь себе, это такая… теорема Пифагора для произвольного треугольника. Она однажды тебя спасёт! Дальше смотри рисунки и ты все поймешь. Один рисунок лучше тысячи слов Разберёшься в ней – будь уверен, что любая задача с треугольником окажется тебе под силу! Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: И причем тут теорема Пифагора? Сейчас поясню. Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов. А что будет, если угол ( displaystyle angle C), скажем, острый? Вроде ясно, что величина ( displaystyle < А если угол ( displaystyle angle C) – тупой? Ну, тогда величина ( displaystyle < Но, опять же, на сколько? И как это связано с величиной ( displaystyle angle C)? Обрати внимание на вот эту добавку к теорему Пифагора: ( displaystyle «-2abcos gamma »). Вот она и «адаптирует» теорему Пифагора под острые и тупые углы треугольника. Сейчас мы докажем теорему косинусов и ты увидишь в теореме косинусов теорему Пифагора своими глазами. Итак, для всякого (и остроугольного, и тупоугольного и даже прямоугольного!) треугольника верна теорема косинусов. Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними. Рассмотрим три случая: И убедимся, что для всех трех случаев теорема косинусов работает! ( displaystyle angle C Он прямоугольный, можно пользоваться теоремой Пифагора: Что такое ( displaystyle AH) и ( displaystyle HB) ? ( displaystyle AH) можно выразить из треугольника (прямоугольного!) ( displaystyle AHC). ( displaystyle AH=bsin gamma ) А вот ( displaystyle BH=a-CH=a-bcos gamma ) (снова из ( displaystyle Delta AHC) ). Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Начинаем точно также: опускаем высоту из точки ( displaystyle A). А теперь, внимание, отличие! ( displaystyle AH=bsin left( <<180>^ ( displaystyle BH=a+bcos left( <<180>^ Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Но тогда ( displaystyle cos gamma =0) и теорема косинусов просто превращается в теорему Пифагора: Ну, например, если у тебя даны две стороны треугольника и угол между ними, то ты прямо сразу можешь найти третью сторону. Или, если тебе даны все три стороны, то ты тут же найдешь косинус любого угла по формуле: И даже, если тебе даны две стороны и угол НЕ между ними, то третью сторону тоже можно найти, решая квадратное уравнение. Правда, в этом случае получается иногда два ответа и нужно соображать, какой же из них выбрать, или оставить оба. Попробуй применять и не бояться – теорема косинусов почти также легка в обращении, как и теорема Пифагора. И приходи к нам на бесплатные вебинары и занятия ( о них ниже). Теорема косинусов (и синусов) — универсальный инструмент при решении треугольников — это теоремы косинусов и синусов. А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам. Этот вебинар из нашего курса подготовки к ЕГЭ по математике (о нем ниже). Вы выучите сами теоремы и научитесь применять их при решении задач первой части. Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком. Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге. · вспомнить формулировки и доказательства теорем синуса и косинуса; · повторить, что значит «решить треугольник» И начнём мы с вами с того, что вспомним формулировку теоремы синусов. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Доказательство. Расширенная теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Доказательство. Что и требовалось доказать. Теперь давайте вспомним теорему косинусов. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними. Доказательство. Частным случаем теоремы косинусов является теорема Пифагора. Давайте рассмотрим прямоугольный треугольник и запишем для него теорему косинусов. Именно поэтому теорему косинусов называют обобщённой теоремой Пифагора. Рассмотрим несколько примеров. Рассмотрим ещё один пример. Рассмотрим ещё один пример. Теперь давайте вспомним, что значит решить треугольник. Определение. Решить треугольник – это значит найти все его элементы (три стороны и три угла) по каким-нибудь известным трём элементам, определяющим треугольник. К задачам такого плана относятся следующие задачи: решение треугольника по трём сторонам; решение треугольника по трём углам; решение треугольника по двум сторонам и углу между ними; решение треугольника по двум сторонам и углу, не лежащего между ними; решение треугольника по стороне и прилежащим к ней углам; решение треугольников по стороне и произвольным двум углам. Рассмотрим каждый вид таких задач отдельно. Начнём с решения треугольника по трём углам. Запишем теорему синусов и косинусов и подумаем, с помощью какой из них можно решить треугольник. Обе эти теоремы содержат длины сторон, поэтому зная только углы треугольника нельзя найти длины сторон треугольника. То есть зная только три угла, решить треугольник нельзя. Попробуем теперь решить треугольник по трём сторонам. Зная длины всех сторон треугольника, по теореме косинусов можно найти косинусы всех углов треугольника. А, зная косинус угла, сам угол найти несложно. Для этого можно воспользоваться либо калькулятором либо таблицами Брадиса. Значит в этом случае решить треугольник можно с помощью теоремы косинусов. Следующим мы рассмотрим решение треугольника по стороне и прилежащим к ней углам. Сразу замечаем, что третий угол найти нетрудно, он равен разности 180 градусов и известных углов. Запишем теорему синусов. Из каждого равенства, мы можем найти сторону треугольника. Таким образом, зная длину одной стороны и величину двух прилежащих к ней углов, можно найти все остальные элементы треугольника, используя теорему синусов. Нетрудно увидеть, что условие: углы прилежащие к стороне здесь не существенно. Поскольку даже если нам известны два любых угла треугольника, то мы всегда можем найти третий угол этого треугольника. Тогда можно сказать, что, зная одну сторону и два любых угла можно решить треугольник с помощью теоремы синусов. Теперь давайте рассмотрим способ решения треугольника по двум сторонам и углу между ними. Третью сторону можно найти с помощью теоремы косинусов. А углы отыскать или с помощью теоремы косинусов, как мы это делали, когда решали треугольник по трём сторонам. Или с помощью теоремы синусов. То есть в таком случае можно решить треугольник используя или теорему синусов или теорему косинусов. Теперь давайте посмотрим, а можно ли решить треугольник, если мы знаем две стороны и угол, который не лежит между ними. Да, можно. Для этого по теореме синусов надо найти второй угол треугольника, а затем и третий угол и по теореме косинусов найти третью сторону треугольника. То есть и в этом случае треугольник можно решить с помощью теоремы синусов и теоремы косинусов. Итак, давайте обобщим. Сегодня на уроке мы с вами вспомнили формулировки и доказательства теорем синуса и косинуса. Повторили, что значит решить треугольник. Теорема Пифагора . В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы. Доказательство . Докажем, что длины сторон произвольного прямоугольного треугольника ABC (рис.1) С этой целью рассмотрим квадрат квадрат со стороной, равной c , изображённый на рисунке 2. Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC (рис.3, рис.4), и площади квадрата со стороной, равной a – b (рис.5). Поэтому справедливо равенство что и требовалось доказать. Теорема косинусов . Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними. Доказательство . Рассмотрим сначала треугольник ABC , у которого углы A и С – острые (рис.6). Докажем, что длины сторон этого треугольника удовлетворяют равенству С этой целью проведём высоту BD из вершины B (рис.7). В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства BD = c sin A, AD = c cos A, DC = b – AD = b – c cos A. Из теоремы Пифагора, применённой к прямоугольному треугольнику BDC , получим Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана. Замечание 1 . Для того, чтобы получить полное доказательство теоремы косинусов, необходимо рассмотреть также и следующие случаи:
Угол A – прямой (рис. 9).
Угол A – тупой (рис.10). Во всех перечисленных случаях доказательства теоремы косинусов проводятся совершенно аналогично тому, как это было сделано для случая острых углов A и C , и мы рекомендуем читателю провести эти доказательства в качестве полезного и несложного упражнения. Замечание 2 . В случае, когда угол A является прямым углом, формула (1) принимает вид откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов. Замечание 3 . Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например, Для произвольного треугольника ABC и его сторон a,b и с (противолежащих к соответствующим вершинам) это равенство можно записать и для двух других сторон: Теорема косинусов используется для решения треугольников в двух главных ситуациях: 1) Когда даны две стороны и угол между ними, а требуется найти последнюю сторону: Иногда репетитор по математике рекомендует использовать теорему косинусов в задаче с двумя данными сторонами и углом, не лежащим между ними. В этом случае а) придется решать квадратное уравнение и отбирать среди полученных корней длину реальной стороны. б) такая ситуация не характерна для задач с ЕГЭ по математике, так как не всегда однозначно задает треугольник. Если угол не лежит между сторонами, то циркулем и линейкой можно построить двух разных треугольника с такими элементами. Теорема косинусов иногда называют расширенной теоремой Пифагора или обобщением теоремы Пифагора, ибо при угле 90 градусов из указанных выше равенств получается Все известные мне доказательства связаны с векторами и координатами. В учебнике Атанасяна оно проводится через координаты точек, а в учебнике Погорелове используется понятие «скалярное произведение векторов». Проведем доказательство по Атанасяну. Оно, как мне кажется больше всего подходит репетитору по математике для работы, так как имеет меньшую зависимость от соседних тем. Даленейшее доказательство строится на алгебраических и тригонометрических выкладках. К ним необходимо добавить знание формулы расстояния между двумя точками. Применяем формулу сокращенного усножения к квадрату суммы: Выносим Любознательному ученику репетитор по математике может показать редкое доказательство теоермы косинусов. Торема косинусов позволяет объяснить весьма полезное на практике свойство диагоналей параллелограмма: Примеры задач, в которых так или иначе можно (или нужно) использовать теорему косинусов: 1) В треугольнике со сторонами 2,3 и 4 найдите длину медианы, проведенную к большей стороне. Полноценная подготовка к ЕГЭ по математике невозможна без решения задач на теорему косинусов. В варианте ЕГЭ она может встретится или в номере B4 или в C4. Постепенно я буду переносить на страницу интересные задачи С4 из моей дидактической базы и с пробных экзаменов. Репетиторы, не забудьте, что в ГИА, как на ЕГЭ, теорема косинусов может проявиться и в первой и во второй части варианта. Колпаков Александр Николаевич, Любознательному ученику репетитор по математике может показать редкое доказательство теорермы косинусов. Проведем в треугольнике ABC высоту СH и запишем АВ=АН+НВ или с=bCosA+aCosB. Если угол B — тупой, то АВ=АН-НВ и с учетом того, что косинусы смежных углов противоположны, снова получим равенство с=bCosA+aCosB. Поэтому оно не зависит от вида треугольника. запишем аналогичные формулы для а и b: Мне этот вариант больше всего нравится. Примерно так я и вывел. Теорема Пифагора — частный случай теоремы косинусов . Здравствуйте! Вы сами такое доказательство нашли? Честь Вам и хвала. Самое интересно, что доказательство не требует координатной и векторной привязки, что позволяет репетитору по математике отрезать часть материала для отстающего ученика, дабы как можно скорее поравняться со школьной программой. Возьму на вооружение. Интересно, Вы репетитор, школьный преподаватель или самородок — любитель математики? Вам от меня личный респект и уважение.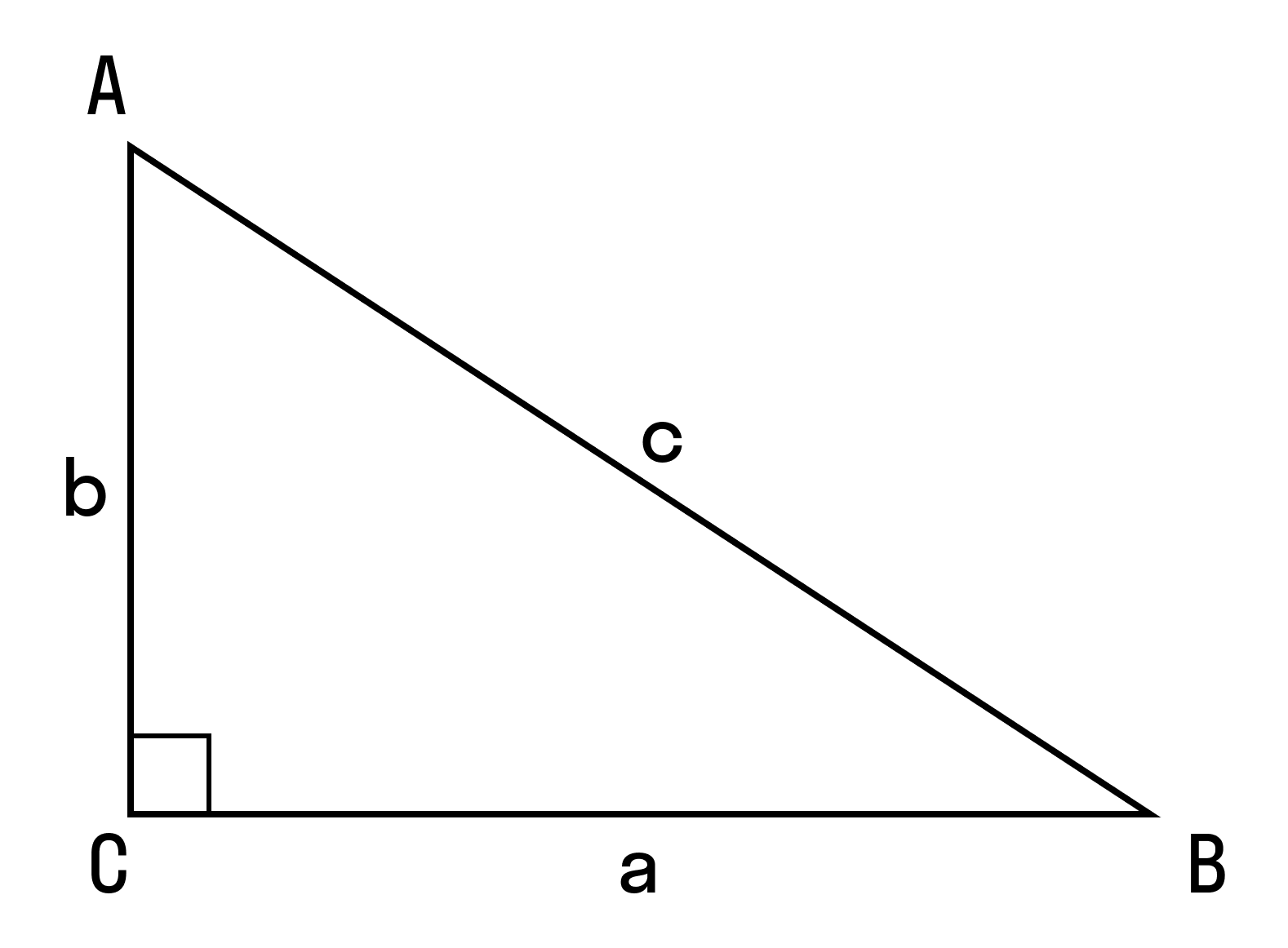
Теорема косинусов
Формулировка теоремы косинусов

Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними
Теорема Пифагора



Рис.3

Рис.4

Рис.5


Формулировка теоремы косинусов для треугольника
 ,
,  , и
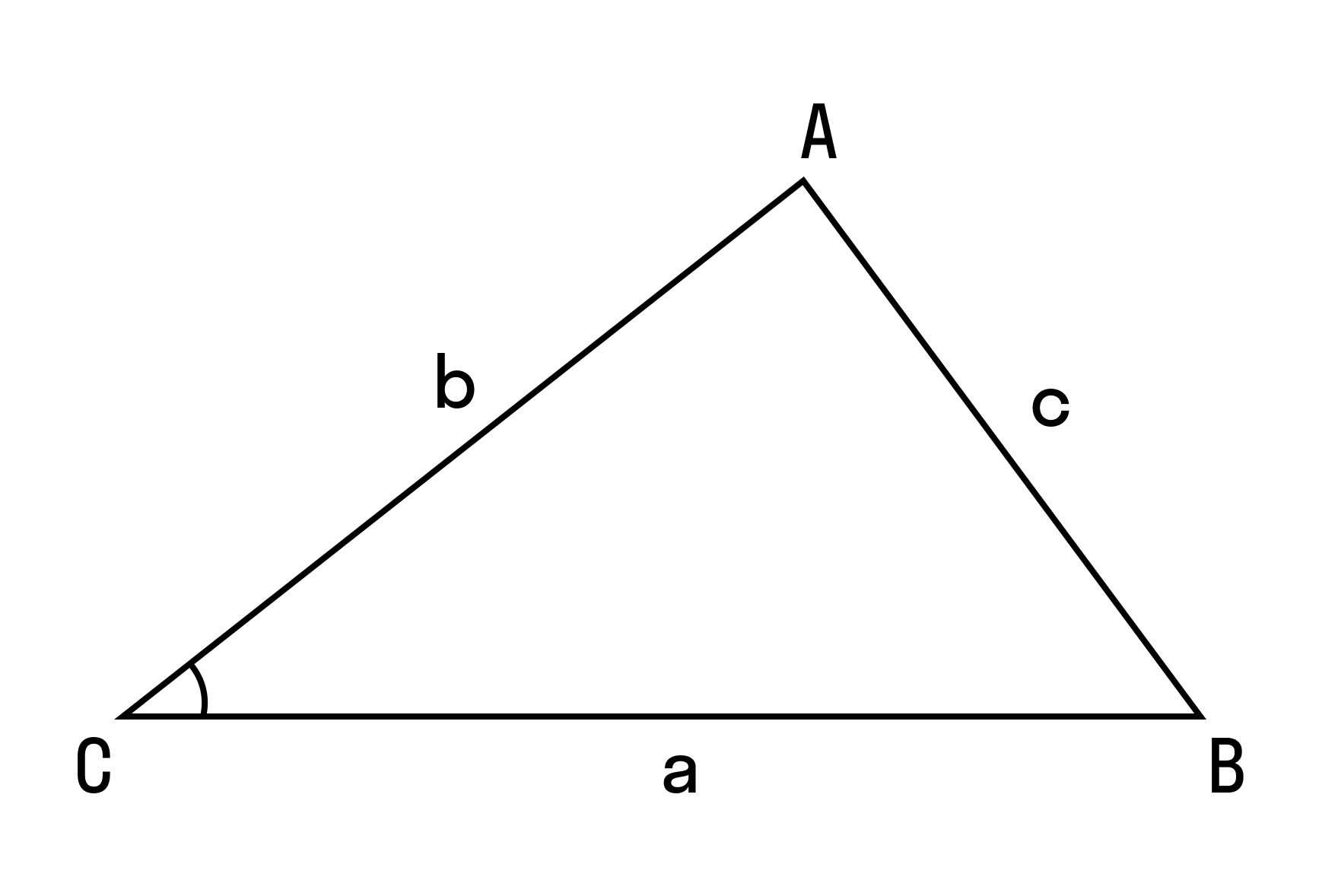
, и  длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.
длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.

 . Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»
. Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.» , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны
, то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны  , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны и
, то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны и  . Выражение для квадрата стороны
. Выражение для квадрата стороны  . Выражение для квадрата стороны получается аналогично:
. Выражение для квадрата стороны получается аналогично:

Классическое доказательство теоремы косинусов.

Формулировка и формула теоремы

Теорема косинусов для остроугольного треугольника.

Доказательство теоремы косинусов для треугольника

Согласно правилам сложения векторов имеем:  . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим
. Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим  . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение:
. Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение:  .
.

 . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол
. Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол  . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.
. Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать. прямой, мы получаем
прямой, мы получаем  прямой, мы получаем , и выражение принимает следующий вид:
прямой, мы получаем , и выражение принимает следующий вид:  . Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.
. Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.Теорема косинусов

a 2 = b 2 + c 2 –
– 2bc cos A (1)





Примеры задач
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.
Применим формулу теоремы, приняв известные стороны за b и c, а неизвестную за a:
a 2 = 5 2 + 9 2 – 2 * 5 * 9 * cos 60° = 25 + 81 – 45 = 61 см 2 . Следовательно, сторона a = √ 61 см ≈ 7,81 см.
Самая большая сторона треугольника равна 26 см, а две другие – 16 и 18 см. Найдите угол между меньшими сторонами.
Примем бОльшую сторону за a. Чтобы найти угол между сторонами b и c, воспользуемся следствием из теоремы:
Теорема косинусов для прямоугольного треугольника
Теорема косинусов для треугольника — формулы, доказательство и решение задач

Геометрическая фигура

Важные линии

Основные законы
Теорема косинусов

Историческая справка

Способы доказательства
Применение для разных видов треугольников

Пример решения задачи

Теорема косинусов (ЕГЭ 2022)
Теорема косинусов — коротко о главном
![]()
Почему теорема косинусов это… теорема Пифагора
![]()
![]()
![]()
Доказательство теоремы косинусов
![]()
Угол С острый
![]()
Читать далее…
Угол С тупой
![]()
Читать далее…
Угол С прямой
![]()
В каких же задачах бывает полезна теорема косинусов?
Бонус: Вебинар на решение задач по теореме косинусов и синусов
Теорема синуса, косинуса. Решение треугольников
Урок 57. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Получите невероятные возможности



Конспект урока “Теорема синуса, косинуса. Решение треугольников”













Теорема Пифагора. Теорема косинусов
 Теорема Пифагорав
Теорема Пифагорав
 Теорема косинусов
Теорема косинусов
Теорема Пифагора
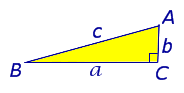
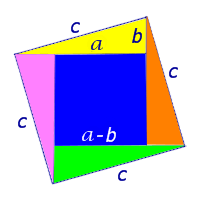
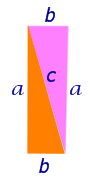
Рис.3
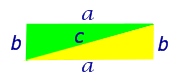
Рис.4
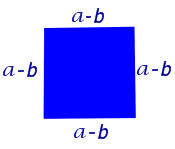
Рис.5
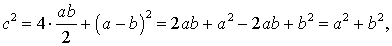
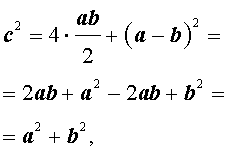
Теорема косинусов
a 2 = b 2 + c 2 –
– 2bc cos A(1)
Теорема косинусов

 Формулировка: Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формулировка: Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.


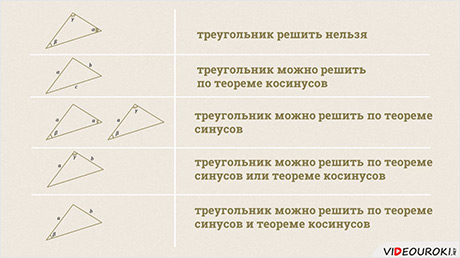
2) Когда даны все три стороны треугольника, а требуется найти его углы: 
 . Как любое обобщение она намного универсальнее и эффективнее частного случая и применяется к большему числу реальных ситуаций (в отличае от искусственных задач ГИА и ЕГЭ по математике, расчитанных на программу 8 класса).
. Как любое обобщение она намного универсальнее и эффективнее частного случая и применяется к большему числу реальных ситуаций (в отличае от искусственных задач ГИА и ЕГЭ по математике, расчитанных на программу 8 класса).Доказательство теоремы косинусов

Докажем равенство для стороны а и угла А. Для этого введем систему координат как показано на рисунке (ось Ох направляется вдоль стороны АС). Точка B при этом получит координаты B (cCosA;cSinA). Это единственный сложный для слабого или среднего ученика факт, который репетитор по математике, работающий по учебнику Атанасяна, должен отдельно рассмотреть. Cложным он является часто по причине того, что не подкреплен в программе достаточным количеством задач и после изучения теоремы косинусов не используется. В случае с данным расположеним точек (когда  — острый) репетитору по математике достаточно обратиться к определению косинуса и синуса острого угла в прямоугольных треугольниках с пунктирными сторонами.
— острый) репетитору по математике достаточно обратиться к определению косинуса и синуса острого угла в прямоугольных треугольниках с пунктирными сторонами.

 за скобку:
за скобку:  . Используем основное тригонометрическое тождество и получаем
. Используем основное тригонометрическое тождество и получаем 

 Проведем в треугольнике ABC высоту BH и запишем АВ=АН+НВ или с=bCosA+aCosB. Если угол B — тупой, то АВ=АН-НВ и с учетом того, что косинусы смежных углов противоположны, снова получим равенство с=bCosA+aCosB. Поэтому оно не зависит от вида треугольника. запишем аналогичные формулы для а и b:
Проведем в треугольнике ABC высоту BH и запишем АВ=АН+НВ или с=bCosA+aCosB. Если угол B — тупой, то АВ=АН-НВ и с учетом того, что косинусы смежных углов противоположны, снова получим равенство с=bCosA+aCosB. Поэтому оно не зависит от вида треугольника. запишем аналогичные формулы для а и b:
a=cCosB+bCosC и b=aCosC+cCosA. Умножая их соответственно на а и b и вычитая из их суммы равнство с=bCosA+aCosB получим равенсто 
 сумма квадратов диагоналей параллелограмма равна сумме квадратов длин его сторон. Для того, чтобы в этом убедиться достаточно записать теорему косинусов для каждой диагонали и сложить полученные равенства.
сумма квадратов диагоналей параллелограмма равна сумме квадратов длин его сторон. Для того, чтобы в этом убедиться достаточно записать теорему косинусов для каждой диагонали и сложить полученные равенства.
2) В том же треугольнике найдите длину биссектрисы, проведенной к большей стороне.
3) В треугольнике АВС отрезок, соединяющий середины АВ и ВС, равен 3 дм, а сторона АВ равна 7дм, угол С равен  . Найдите ВС.
. Найдите ВС.
4) Центр окружности, вписанной в прямоугольный треугольник АВС с прямым углом С находится на расстоянии  и
и  от вершин А и В. Надите катеты треугольника.
от вершин А и В. Надите катеты треугольника.
репетитор по математике в Москве. Подготовка к ЕГЭ
a=cCosB+bCosC и b=aCosC+cCosA. Умножая их соответственно на а и b и вычитая из их суммы равенство с=bCosA+aCosB, умноженное на с, получим классический вид теоремы косинусов.