Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №18. Компланарные векторы. Векторный метод решения задач
Перечень вопросов, рассматриваемых в теме:
– какие векторы называются компланарными и их изображение на чертежах
-определение компланарных векторов.
– признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.
– основы векторного метода решения задач.
Основная литература:
Атанасян Л.С. и др. Геометрия. Учебник для 10-11классов – М.: Просвещение, 2017. C. 77-85.
Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь-конспект по геометрии для 10 класса. 2016. С.88-93.
Теоретический материал для самостоятельного изучения:
Давайте вспомним основные определения по теме «Векторы». В этом поможет следующее задание: установите соответствие между понятием и его определением.
Противоположно направлены и их длины равны.
Сонаправлены и их длины равны.
Лежат на одной или параллельных прямых
Появилось новое понятие о векторах в пространстве, которого не было на плоскости – компланарность векторов. С определения компланарных векторов и начинаются главные отличия векторов в планиметрии и стереометрии.
Компланарные векторы.
Определение2.Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Рассмотрим некоторые случаи:
1 случай. Любые два вектора всегда будут компланарными, ведь через них
можно провести прямые, а через две прямые всегда можно провести
единственную плоскость.
2 случай. Три вектора будут компланарными если среди них есть пара коллинеарных
векторов. Тогда через один из коллинеарных векторов и вектор не коллинеарный ему
можно провести плоскость. А для второго из коллинеарных векторов легко
изобразить равный в этой плоскости.
3 случай. Если хотя бы один из трёх векторов является нулевым, то эти три вектора компланарны
Из планиметрии: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
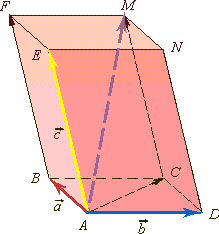
Следующая теорема выражает признак компланарности трех векторов. Теорема (признак) Если вектор  можно представить в виде
можно представить в виде  = х
= х  + у
+ у , где х и у – некоторые числа, то векторы
, где х и у – некоторые числа, то векторы  ,
,  и
и  компланарны.
компланарны.
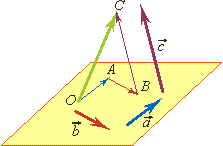
Для сложения трёх некомпланарных векторов можно пользоваться правилом параллелепипеда. Отложим от произвольной точки О векторы  =
= ,
,  =
= ,
,  =
=  и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были рёбрами.
и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были рёбрами.
Тогда ОD – диагональ этого параллелепипеда равна сумме векторов ,
,  и
и  . Если вектор можно представить в виде суммы:
. Если вектор можно представить в виде суммы:  = х
= х  + у
+ у  + z
+ z , то говорят, что вектор d разложен по векторам
, то говорят, что вектор d разложен по векторам  ,
,  и
и  . Числа х, у, z называют коэффициентами разложения.
. Числа х, у, z называют коэффициентами разложения.
Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Часть 2. Векторный метод решения задач
Векторный метод решения задач – один из наиболее общих методов решения геометрических задач. Векторное решение стереометрических задач значительно проще их решения средствами элементарной геометрии.
Рассмотрим следующую задачу: Доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.
Пусть ABCD – данная трапеция, M и N – середины оснований BC И AD, а O – точка пересечения прямых AB и CD.
Докажем, что точка О лежит на прямой МN.
Условие задачи переводится на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык.
Решением задач векторным методом занимались ученые: Уильман Гамильтон Иога́нн Берну́лли, Пьер Ферма, Рене Декарт, Леонард Эйлер.
Примеры и разбор решения заданий тренировочного модуля:
Задача. В параллелепипеде АВСDА1В1С1D1 М —точка пересечения диагоналей грани A1B1C1D1, точка K — середина ребра ВВ1. Докажите, что прямые А1В1, KМ и ВС1 параллельны некоторой плоскости.

Решение. Введем векторы: 

 . Векторы
. Векторы  некомпланарны.
некомпланарны.
Разложим векторы  и
и  по векторам
по векторам . Получим:
. Получим:


 +
+ =
=  .
.
Тогда векторы  =
= 
 +
+  компланарны. Следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А1В1, KМ и ВС1.
компланарны. Следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А1В1, KМ и ВС1.
Компланарные векторы
Вы будете перенаправлены на Автор24
Понятие компланарности векторов
Для начала рассмотрим, какие вектора называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Рассмотри, компланарны ли векторы a, b и c на следующем примере. Пусть нам даны три вектора $overrightarrow
Пары векторов $overrightarrow
Если два из этих векторов, к примеру $overrightarrow
Если $overrightarrow
Для дальнейшего рассмотрения напомним следующую теорему.
Произвольный вектор $overrightarrow
$ можно разложить по двум неколлинеарным векторам $overrightarrow
Теоремы, связанные с условием компланарности трех векторов
Если один из трех данных векторов можно разложить по двум другим векторам, то есть
Доказательство.
Здесь возможны два случая.
Теорема доказана.
Готовые работы на аналогичную тему
Доказательство.
[overrightarrow
Причем это разложение единственно.
Которое также единственно.
Теорема доказана.
Признак и критерий компланарности векторов

Рисунок 1. Условие компланарности векторов. Автор24 — интернет-биржа студенческих работ
Пример задачи
Пусть нам дан куб $ABCDA_1B_1C_1D_1$. Разложите вектор $overrightarrow

Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ
Решение.
Так как плоскости $(ABC)$ и $<(A>_1B_1C_1)$ параллельны, и векторы $overrightarrow
Используя свойства сложения двух векторов, получим
Ответ: $overrightarrow
Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.

Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Так как векторы $overrightarrow
Так как векторы $overrightarrow
Так как векторы $overrightarrow
Доказать, что векторы с координатами $left(1, 13, 2right), left(3, -5, 2right)и (5,-1,4)$ компланарны.
Решение.
Применим признак компланарности трех векторов.

Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ
Следовательно, это векторы компланарны, ч. т. д.
Компланарные векторы, исследование системы векторов на компланарность.
В этой статье мы поговорим о компланарности векторов. Сначала вспомним определение компланарности и получим необходимое и достаточное условие компланарности трех векторов в трехмерном пространстве. Далее разберемся с задачей исследования системы из n векторов на компланарность, рассмотрим решения характерных примеров.
Навигация по странице.
- Необходимое и достаточное условие компланарности трех векторов.
- Исследование системы векторов на компланарность, примеры и решения.
Необходимое и достаточное условие компланарности трех векторов.
Напомним определение компланарных векторов.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Два вектора  и
и  трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы
трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы  и
и  соответственно. Проведем через начало вектора
соответственно. Проведем через начало вектора  прямую b1 , параллельную прямой b , а через начало вектора
прямую b1 , параллельную прямой b , а через начало вектора  прямую a1 , праллельную прямой a . Плоскости, образуемые прямыми a и b1 , а так же прямыми b и a1 , параллельны по построению, а векторы
прямую a1 , праллельную прямой a . Плоскости, образуемые прямыми a и b1 , а так же прямыми b и a1 , параллельны по построению, а векторы  и
и  принадлежат им. Следовательно, векторы
принадлежат им. Следовательно, векторы  и
и  компланарны.
компланарны.
А как же определить, являются ли три вектора компланарными?
Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.
Для компланарности трех векторов  и
и  трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Пусть  , докажем что векторы
, докажем что векторы  и
и  компланарны.
компланарны.
Так как 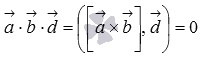 , то векторы
, то векторы  и
и  перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор
перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор  перпендикулярен и вектору
перпендикулярен и вектору  и вектору
и вектору  . Следовательно, векторы
. Следовательно, векторы  и
и  компланарны, так как перпендикулярны одному вектору
компланарны, так как перпендикулярны одному вектору  .
.
Пусть теперь векторы  и
и  компланарны, докажем равенство нулю смешанного произведения
компланарны, докажем равенство нулю смешанного произведения  .
.
Так как векторы  и
и  компланарны, то вектор
компланарны, то вектор  перпендикулярен каждому из них, следовательно, скалярное произведение вектора
перпендикулярен каждому из них, следовательно, скалярное произведение вектора  на
на  равно нулю, что означает равенство нулю смешанного произведения
равно нулю, что означает равенство нулю смешанного произведения  .
.
Итак, теорема полностью доказана.
Покажем применение доказанного условия компланарности трех векторов к решению задач.
Компланарны ли векторы  , заданные в прямоугольной системе координат.
, заданные в прямоугольной системе координат.
Вычислим их смешанное произведение по координатам:

Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.
Необходимое и достаточное условие компланарности векторов можно использовать для проверки принадлежности четырех точек пространства А, В, С и D одной плоскости. Для этого находим координаты векторов  и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.
и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.
Принадлежат ли точки 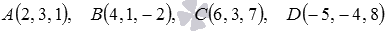 одной плоскости?
одной плоскости?
Найдем координаты векторов  (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца):
(при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца):

Теперь вычисляем смешанное произведение этих векторов

Так как смешанное произведение векторов отлично от нуля, то векторы  не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.
не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.
Исследование системы векторов на компланарность, примеры и решения.
А как же быть, если требуется установить компланарность системы векторов, число векторов которой больше трех?
Давайте ответим на этот вопрос и получим условие компланарности системы из n векторов трехмерного пространства.
В предыдущем пункте мы показали, что для компланарности трех векторов  и
и  необходимо и достаточно равенство нулю их смешанного произведения:
необходимо и достаточно равенство нулю их смешанного произведения:  . Так как смешанное произведение трех векторов в координатной форме представляет собой определитель матрицы, строками которой являются координаты векторов
. Так как смешанное произведение трех векторов в координатной форме представляет собой определитель матрицы, строками которой являются координаты векторов  и
и  , то условие компланарности можно записать в виде
, то условие компланарности можно записать в виде  . Вспомнив понятие ранга матрицы, последнее равенство можно интерпретировать следующим образом: ранг матрицы, строками которой являются координаты компланарных векторов
. Вспомнив понятие ранга матрицы, последнее равенство можно интерпретировать следующим образом: ранг матрицы, строками которой являются координаты компланарных векторов  и
и  , меньше трех.
, меньше трех.
Обобщив последнее утверждение, мы получим необходимое и достаточное условие компланарности системы из n векторов трехмерного пространства: для компланарности системы из n векторов трехмерного пространства необходимо и достаточно, чтобы ранг матрицы, строками которой являются координаты векторов системы, был меньше трех.
Компланарны ли векторы
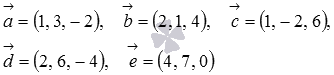
Составим матрицу, строками которой примем координаты данных векторов

Сразу легко отыскать минор второго порядка, отличный от нуля, 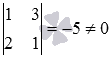 .
.
Переберем окаймляющие его миноры третьего порядка:

Все они равны нулю, следовательно, ранг матрицы равен двум, поэтому, векторы заданной системы векторов компланарны в силу выполнения необходимого и достаточного условия компланарности.
Компланарные векторы
- Что такое компланарные векторы
- Условия компланарности и линейная зависимость векторов
- Линейная зависимость
- Условия компланарности
- Теоремы, связанные с условием компланарности трех векторов
- Пример задачи на компланарность векторов
Что такое компланарные векторы
Векторы называются компланарными, если лежат в одной или параллельных плоскостях.
Это определение справедливо только для трех и более векторов, так как для двух направленных отрезков всегда можно найти плоскость, параллельную им.
Условия компланарности и линейная зависимость векторов
Среди условий компланарности векторов встречается понятие линейной зависимости, которое следует разобрать перед тем, как перейти непосредственно к условиям.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Линейная зависимость
Линейно зависимыми называются вектора (overline , которые можно составить в линейную комбинацию, равную нулю: (lambda_1cdotoverline
, которые можно составить в линейную комбинацию, равную нулю: (lambda_1cdotoverline
Линейная комбинация — вектор, составленный из суммы векторов (overline и коэффициентов разложения (lambda_<1,>;lambda_2,;dots;,;lambda_n.)
и коэффициентов разложения (lambda_<1,>;lambda_2,;dots;,;lambda_n.)
Существует пять критериев и свойств линейной зависимости векторов:
- Хотя бы один из векторов можно представить в виде линейной комбинации других.
- В n-мерном пространстве любые n+1 векторов линейно зависимы.
- Хотя бы один из векторов — нулевой.
- Если часть системы векторов линейно зависимы, то это справедливо и для остальных.
- Если одна система векторов может быть выражена через другую и содержит больше векторов, то такая система линейно зависима.
Условия компланарности
Для неограниченного числа векторов справедливо следующее: если среди них есть не более двух линейно независимых векторов, то они компланарны.
На практике чаще всего встречаются задачи с тройками векторов. Для них существуют и другие условия компланарности:
- Если три вектора линейно зависимы, то они компланарны.
- Смешанное произведение компланарных векторов равняется нулю.
Теоремы, связанные с условием компланарности трех векторов
Правило, согласно которому три вектора компланарны, если их смешанное произведение равно нулю, проистекает из теоремы. Его также называют признаком и критерием компланарности векторов. Доказать данное утверждение можно следующим образом:
Пусть смешанное произведение ((overline atimesoverline b)cdotoverline c=0) . Векторы ((overline atimesoverline b)) и (overline c) — перпендикулярны, так как их скалярное произведение равняется нулю.
В то же время, результатом векторного произведения является вектор, перпендикулярный перемножаемым. Таким образом, векторы overline a,overline b,overline c перпендикулярны одному и тому же вектору (overline atimesoverline b), то есть лежат в параллельных плоскостях. Значит, векторы компланарны.
Для проверки, к доказательству данной теоремы можно подойти с другой стороны:
Пусть векторы overline a,overline b,overline c компланарны.
Необходимо доказать, что их смешанное произведение ((overline atimesoverline b)cdotoverline c) равняется нулю. Так как данные вектора компланарны, то ((overline atimesoverline b)) перпендикулярен каждому из них.
Отсюда следует, что его скалярное произведение с вектором overline c будет равняться нулю. Это, в свою очередь, означает, что смешанное произведение ((overline atimesoverline b)cdotoverline c=0.)
Пример задачи на компланарность векторов
Задача
Даны точки A(1, 2, -1), B(0, -1, 5), C(-1, 2, 1) и D(2, 1, 3). Проверить, принадлежат ли они одной плоскости.
Решение
Сперва необходимо построить на основе имеющихся точек векторы (overline
Чтобы проверить, принадлежать ли точки одной плоскости, необходимо найти смешанное произведение полученных векторов. Если оно равняется нулю, то векторы компланарны, следовательно, точки лежат в одной плоскости. В противном случае ответ на поставленный в условии вопрос будет отрицательным.
Смешанное произведение рассчитывается по формуле нахождения определителя матрицы:
Полученное число не равно нулю, следовательно, векторы некомпланарны. Это значит, что точки не лежат в одной плоскости.
Какие векторы называют компланарными
Компланарные векторы – это векторы, которые лежат в одной плоскости, или параллельны какой-либо плоскости.
Рассмотрим три вектора в трехмерном пространстве. Любые два из них будут компланарными всегда. Поэтому, компланарность проверяют минимум для трех векторов.
Почему любые два вектора всегда компланарны
Поясним факт, что любые два вектора будут компланарными.
Для начала вспомним, какие векторы называют равными. Равны векторы, у которых совпадают три характеристики: длина, направление, соответственные координаты.
При параллельном переносе вектор не поворачивается. Этот новый вектор ( vec
[ vec = vec
Если два вектора равны, то вместо одного из них мы сможем использовать второй, когда это будет удобным для нас.
Проделаем теперь те же операции с каким-либо другим вектором ( vec ). В результате получим вектор ( vec
Любые два вектора можно параллельным переносом сдвинуть так, чтобы совместить их начальные, или конечные точки. Значит, через эти векторы можно провести пересекающиеся прямые. А такие прямые будут лежать в одной плоскости.

Таким образом, любые два вектора всегда компланарны.
Например, любые два орта Декартовой прямоугольной системы координат компланарны, а тройка ортов – некомпланарные векторы. Подробнее об ортах тут (откроется в новой вкладке).
Условие компланарности
Найдем смешанное произведение трех векторов.
Смешанное произведение обозначают так:
[ left( vec , vec , vec <с>right) ]
Если такое произведение будет равно нулю, то три вектора компланарные.
Условие компланарности векторов:
[large boxed < left( vec, vec , vec
Как вычислить смешанное произведение
- Нужно любые два вектора перемножить векторным способом, в результате получим новый вектор.
- Этот новый вектор умножаем скалярным способом на оставшийся третий вектор.
Смешанное произведение можно обозначить еще одним способом:
Результат смешанного произведения – это число. Если число равно нулю, то векторы компланарны.
Как применять смешанное произведение
Если три вектора не компланарны, то на них, как на сторонах, можно построить параллелепипед, или пирамиду.
С помощью смешанного произведения можно рассчитывать объемы параллелепипедов или треугольных пирамид, построенных на трех некомпланарных векторах.
Примечание:
Определитель может быть равен отрицательному числу. А объем может быть либо нулевым, либо положительным. Поэтому, если при вычислении объема определитель будет равен отрицательному числу, знак минус не учитываем.

Рисунок 2 поясняет, как с помощью векторов на ребрах параллелепипеда можно рассчитать его объем

Рисунок 3 поясняет, как с помощью векторов на ребрах пирамиды можно рассчитать ее объем
Смешанное произведение векторов в физике — работа вращающей силы
Пусть цилиндрическое тело вращается под действием силы. Ось вращения проходит через ось симметрии тела.
Работа вращающей силы – это смешанное произведение векторов ( vec
[ large boxed < dA = left( vec
Пояснения:
Линейная скорость – это векторное произведение радиуса окружности на угловую скорость:
Расстояние, ( vec
[ vec
Небольшая работа dA – это скалярное произведение вектора силы на вектор перемещения
[ dA = left( vec
Компланарные векторы



Определение 7. Векторы называются компланарными, если их можно отложить в одной плоскости.
Свойства компланарных векторов.
1 0 . Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.
2 0 . Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения.
3 0 . Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других.
Доказательство. Þ Пусть векторы 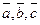 компланарны. Возможны два случая.
компланарны. Возможны два случая.
1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть  и
и  коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть
коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть 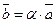 . Тогда
. Тогда 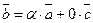 , т.е. вектор
, т.е. вектор  есть линейная комбинация векторов
есть линейная комбинация векторов  и
и 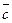 .
.
2) Данные векторы попарно не коллинеарны. Отложим их от одной точки О. Пусть 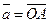 , , 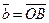 , , 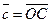 . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда 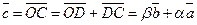 , т.е. вектор , т.е. вектор  есть линейная комбинация векторов есть линейная комбинация векторов  и и  . . |
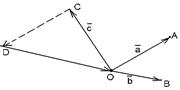 Рис. 7 Рис. 7 |
Ü Пусть 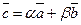 . По свойствам 1 0 и 2 0 следует, что вектор
. По свойствам 1 0 и 2 0 следует, что вектор 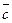 компланарен с векторами
компланарен с векторами  и
и  .
.
4 0 . Если векторы  и
и  не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
5 0 . Из свойств 1 0 и 2 0 следует, что множество всех возможных компланарных векторов относительно операций сложения векторов и умножения вектора на действительное число ведёт себя так же, как множество всех коллинеарных векторов и как множество всех геометрических векторов. Кроме того, для задания множества всех возможных компланарных векторов достаточно задать любые два не коллинеарные из них.
Компланарные векторы – определение, признаки и свойства





10 класс
Материалы к зачетной работе по теме
“Перпендикулярность прямых и плоскостей. Векторы в пространстве“
Параллельный перенос
Введём на плоскости декартовы координаты xОу. Преобразование некоторой фигуры F, при котором произвольная ее точка А (х;у) переходит в другую точку А (х+a; y+b), где а и b постоянные, называется параллельным переносом;
Параллельный перенос есть движение. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
Понятие вектора
Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.
Геометрически векторы изображаются направленными отрезками.
Направленный отрезок называется вектором.
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения);
2 )направлением;
3) длиной («модулем вектора»).
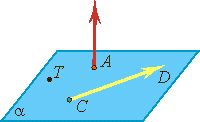
Если начало вектора — точка А, а его конец — точка В, то вектор обозначается 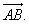 или
или 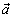 .
.
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Обозначается: 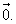 .
.
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора 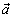 .
.
Обозначается  .
.
векторы
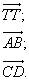


Два вектора называются равными, если они совмещаются параллельным переносом.
АВСD — параллелограмм, 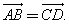

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если векторы 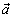 и
и 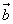 коллинеарны и их лучи сонаправлены, то векторы
коллинеарны и их лучи сонаправлены, то векторы 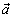 и
и 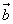 называются сонаправленными.
называются сонаправленными.
Обозначаются 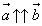 .
.
Если векторы 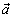 и
и 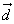 коллинеарны, а их лучи не являются сонаправленными, то векторы
коллинеарны, а их лучи не являются сонаправленными, то векторы 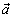 и
и 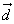 называются противоположно правленными.
называются противоположно правленными.
Обозначаются 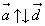 . Нулевой вектор условились считать сонаправленным с любым вектором.
. Нулевой вектор условились считать сонаправленным с любым вектором.

коллинеарные векторы: 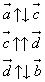
Свойство коллинеарных векторов
Правило многоугольника применяется, если нужно найти сумму трех или большего числа векторов.
Сумма нескольких векторов не зависит от того, в каком порядке они складываются.
От произвольной точки О отложен вектор 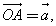 затем от точки А отложен вектор
затем от точки А отложен вектор 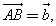 и, наконец, от точки В отложен вектор
и, наконец, от точки В отложен вектор  В результате получается вектор
В результате получается вектор 
Умножение вектора на число
Произведением ненулевого вектора 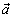 на число k называется такой вектор,
на число k называется такой вектор, 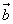 , длина которого равна,
, длина которого равна, 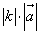 , причем векторы
, причем векторы 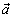 и
и 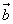 сонаправлены при
сонаправлены при 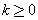 и противоположно направлены при k
и противоположно направлены при k
Признак компланарности трех векторов
Если вектор 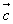 можно разложить по векторам
можно разложить по векторам 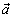 и
и 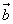 , т.е. представить в виде
, т.е. представить в виде
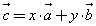 ,
,
где х и у — некоторые числа, то векторы 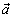 ,
, 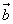 и
и 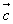 компланарны.
компланарны.
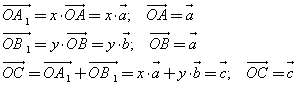

Правило параллелепипеда
Сумма трех некомпланарных векторов равна вектору, изображаемому направленной диагональю параллелепипеда, построенному на этих векторах.
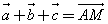
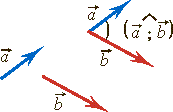
Угол между двумя векторами
Углом между двумя направлениями в пространстве называется величина наименьшего угла между любыми лучами этих направлений с общим началом.
Угол между лучами  обозначается
обозначается  . По определению угол между двумя направлениями находится в промежутке [0°; 180°].
. По определению угол между двумя направлениями находится в промежутке [0°; 180°].
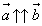
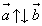
Базис вектора. Разложение вектора на плоскости по двум некомпланарным векторам
Теорема: Любой вектор 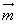 на плоскости может быть представлен, и притом единственным образом, в виде двух любых неколлинеарных векторов
на плоскости может быть представлен, и притом единственным образом, в виде двух любых неколлинеарных векторов 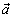 и
и 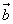 :
:

Числа x и y называются координатами вектора. Векторы 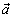 и
и 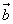 называются базисом вектора
называются базисом вектора 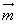 на плоскости.
на плоскости.
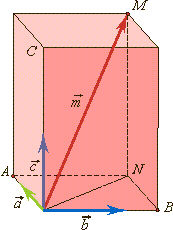
Разложение вектора по трем некомпланарным векторам
Базисом пространства называют любые три некомпланарных вектора, взятые в определенном порядке
Теорема: Любой вектор 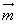 на плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых неколлинеарных векторов
на плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых неколлинеарных векторов 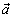 ,
, 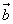 и
и 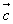 :
:
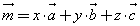
Числа x, y и z называются координатами вектора  в данном базисе. В этом случае пишут:
в данном базисе. В этом случае пишут:
Действия над векторами, заданными своими координатами
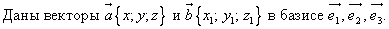
Сложение
Вычитание
Умножение
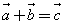
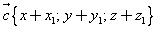
При сложении векторов их соответстветственные координаты
складываются.


При вычитании векторов их соответстветственные координаты
вычитаются.

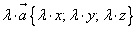
При умножении вектора на число все его координаты умножаются на это число.