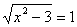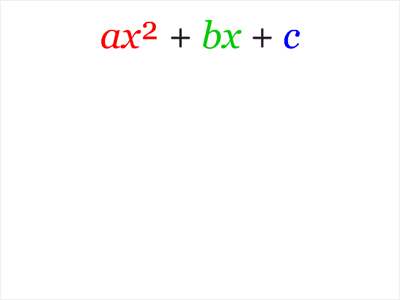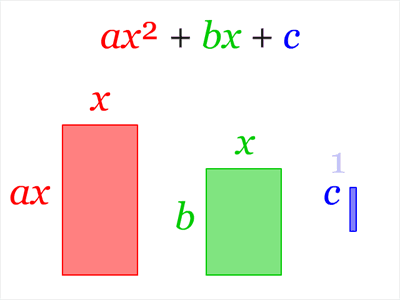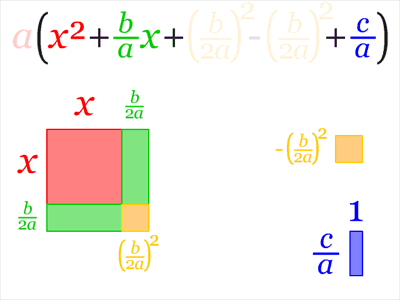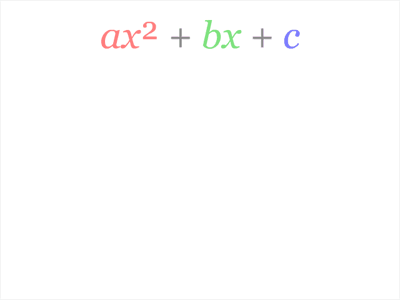Описание и решение неравенств с двумя переменными

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №42. Линейные уравнения и неравенства с двумя переменными

Перечень вопросов, рассматриваемых в теме:

• Решение уравнений, неравенств, систем уравнений и систем неравенств с двумя переменными;
• Изображение в координатной плоскости множества решений уравнений, неравенств, систем уравнений, систем неравенств;
• Нахождение площади получившейся фигуры.

Глоссарий по теме

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными, где a, b и c — некоторые числа (a ≠ 0 , b ≠0), а, х и у — переменные.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Историческая справка

Уравнения, а также системы уравнений имеют давнюю историю. Нам известно, что уже в Древнем Вавилоне и Индии повседневные задачи, связанные с земляными работами или планированием военных расходов, а также астрономическими наблюдениями решались с помощью уравнений и их систем.

В то время еще не существовало привычного нам формального языка математики. Вавилоняне, также, как и индусы не использовали в своих трактатах привычные нам «икс» и «игрек». Не обозначали степень надстрочными индексами. И т.д. Их уравнения записаны в виде текстовых задач. Также, как и решения, не похожи на современные, а скорее напоминают цепочку логических рассуждений.

Вместе с тем, если перевести в привычный нам вид те уравнения, которые умели решать в Древнем Вавилоне, то мы увидим: . И в древнем индийском манускрипте «Ариабхаттиам», датируемом 499 годом нашей эры, также встречаются задачи, решаемые с помощью квадратных уравнений. Индийские мудрецы (слово ученый тоже еще не существовало) уже не ограничивались решением конкретных житейских задач, но и работали над решением квадратного уравнения в общем виде.

Привычный нам вид уравнения обретают только в конце шестнадцатого века, благодаря трудам Франсу Виета (1540 – 1603 гг.). Именно он, помимо прочих своих научных достижений обладает и неофициальным титулом «создатель алгебры». Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».

Актуализация знаний

1.Найдите уравнения, которые являются линейными.

4х + 5у = 10; ; у = 7х +4

Ответ: 4х + 5у = 10; у = 7х +4

Сегодня на уроке мы вспомним что такое линейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое линейным уравнением и неравенством.

1. Линейные уравнения с двумя переменными.

Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.

Решением уравнения ах + by +с =0, где а,b,с – некоторые числа, называется пара значений обращающая уравнение в верное числовое равенство.

Если одновременно а и b, то уравнение ах + by +с =0 является уравнением некоторой прямой. Для построения прямой достаточно найти две точки этой прямой.

Построить график уравнения 2х+у =1

На координатной плоскости отметим точки с координатами (0;1) и (2;-3). Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1.

1. Линейные неравенства с двумя переменными.

Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с 0, где х и у – переменные, а, b, c – некоторые числа.

Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.

Является ли пара (2;1) решением неравенства 5х + 2у > 4 . Является, тк при подстановке в него вместо х числа 2, а вместо у числа 1 получается верное равенство 10 + 2 > 4.

Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.

Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.

1. Уравнение 3х – 2у +6 = 0 является уравнением прямой, проходящей через точки(- 2; 0) и (0; 3).
2. Пусть точка М₁(х_1,у₁) лежит в заштрихованной полуплоскости (ниже прямой 3х – 2у +6 = 0, а М₂(х_1,у₂)лежит на прямой 3х – 2у +6 = 0_. Тогда 2у₂ – 3х₁ – 6 = 0, а 2у₁ – 3х₁ – 6 0 штриховкой (рис. 1)

Рисунок 1 – решение неравенства 3х – 2у +6 > 0

Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение ах + by +с =0, графиком которого является прямая при условии, что и . Прямая разбивает плоскость на две полуплоскости. Одна из них является графиком неравенства ах + bу + с 0

Чтобы решить неравенство ах + bу + c 0, достаточно взять какую-нибудь точку М₁(х₁; у₁), не лежащую на прямой aх + bу + c = 0, и определить знак числа aх₁ + bу₁ + c.

Линейные неравенства с двумя переменными и их системы

Линейное неравенство с двумя переменными и его решение

Неравенство вида ax+by $ begin lt \ gt \ le \ ge end $ c , где a, b, c – данные числа, называется линейным неравенством с двумя переменными x и y.

Например: $2x+5y lt 6; -x+1, 5y ge 0; frac<1> <2>x-8y gt 7$

Решением неравенства с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это неравенство в истинное выражение.

Например: для неравенства $2x+5y lt 6$

пара (-1;-2) является решением, т.к. $2cdot(-1)+5 cdot (-2) = -12 lt 6$ – истина

пара (1;2) не является решением, т.к. $2cdot1+5cdot2=12 notlt 6$ – ложь

Графическое представление линейного неравенства с двумя переменными

Графическим представлением линейного неравенства с двумя переменными вида ax+by$ begin lt \ gt \ le \ ge end $ c является полуплоскость с границей ax+by = c .

Для строгого неравенства граница не входит в представление, для нестрогого неравенства – входит.

Графическое решение системы линейных неравенств с двумя переменными

Графическим решением системы линейных неравенств с двумя переменными является пересечение их графических представлений на плоскости.

Пересечение двух множеств – это множество, которому принадлежат только те элементы, которые одновременно входят в оба множества.

Пересечение обозначают знаком $cap$.

Найдём графическое решение системы линейных неравенств:

Решением является треугольник ABC, где A(-1;2), B(0;4), C(2;0).

Примеры

Пример 1. Найдите графическое представление линейного неравенства:

Представление – полуплоскость под границей, сама граница не входит

Представление – полуплоскость под границей, сама граница входит

Представление – полуплоскость справа от границы, сама граница входит

Представление – полуплоскость под границей, сама граница не входит

Пример 2*. Найдите графическое решение системы линейных неравенств:

Решением является квадрат ABCD, где A(-3;-1), B(0;2), C(3;1), D(0;-4)

Пример 3*. Автоперевозчику поступил заказ на перевозку 30 т груза. У него есть 5 машин грузоподъёмностью 3 т и 5 машин грузоподъёмностью 5 т.

Расход топлива для каждого типа грузовиков соответственно 20 и 24 л, общий расход не должен превышать 170 л.

Подберите состав грузовиков для выполнения заказа.

Пусть x – количество грузовиков по 3т, y – по 5т.

По условию задачи:

$$ 3x+5y ge 30 \ 20x+24y le 170 \ x le 5 \ y le 5 end right.> $$

Решением системы неравенств является заштрихованный треугольник. Единственным целочисленным решением является точка A(2;5) Таким образом, для выполнения заказа нужно 2 грузовика по 3т и 5 грузовиков по 5т.

Их суммарная грузоподъёмность: $3 cdot 2+5 cdot 5 = 31 gt 30$ достаточна

Суммарный расход топлива: $ 20 cdot 2+24 cdot 5 = 160 lt 170 $ не превышает лимит

Ответ: 2 грузовика по 3т и 5 грузовиков по 5т

Неравенства с двумя переменными

Урок 19. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Неравенства с двумя переменными”

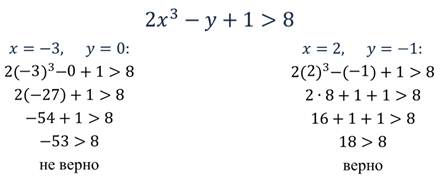
Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.

Тогда пара значений (2; -1) является решением данного неравенства, но это не единственное решение.

Проверить, является ли пара чисел (-2; 3) решением неравенств.

Подставим пару этих значений в каждое неравенство и проверим, обратятся ли они в верные числовые неравенства:

Получили, что в первом и во втором случаях – верное неравенство, а в третьем – пара чисел (-2; 3) не является решением данного неравенства.

Найти два каких-нибудь решения неравенства:

Очевидно, что х может быть любым числом.

Среди множества решений данного неравенства будут пары чисел: (5; 17) и (-3; 8).

Так как неравенство с двумя переменными имеет множество решений, то их сложно перечислить. Увидеть множество решений неравенства с двумя переменными позволяет график.

Изобразим на координатной плоскости множество точек, заданных неравенством:

Построим график уравнения:

Графиком является прямая и для её построения достаточно двух точек:

Возьмём на прямой некоторую точку М с координатами (). Если мы возьмём точку К выше прямой, видно, что её абсцисса = , а вот ордината > . Тогда получаем, что координаты точки К не удовлетворяют неравенству. Если же взять точку, расположенную ниже прямой, с абсциссой = , то видно, что её ордината будем . Тогда получаем, что координаты точки удовлетворяют неравенству. Если же взять точку N, расположенную ниже графика, с абсциссой = , то видно, что её ордината будем Оцените видеоурок

Неравенства с переменными, их частные и общее решение.

Если в школьном курсе математики и алгебры отдельно выделить тему «неравенства», то основную часть времени постигаются азы работы с неравенствами, которые содержат в своей записи переменную. В данной статье мы разберем, что такое неравенства с переменными, скажем, что называют их решением, а также разберемся, как записываются решения неравенств. Для пояснения будем приводить примеры и необходимые комментарии.

Навигация по странице.

• Что такое неравенства с переменными?
• Неравенства с одной переменной.
• Неравенства с двумя переменными.
• Неравенства с тремя и большим числом переменных.
• Решения неравенства: частное, общее и просто решение.
• Как записать общее решение неравенства?

Что такое неравенства с переменными?

Мы уже знакомы с числовыми неравенствами. Они представляют собой два числовых выражения, между которыми находится один из знаков неравенства. Если же хотя бы одно из этих числовых выражений заменить на выражение с переменными, то мы получим так называемое неравенство с переменными.

Итак, мы только что определили неравенства с переменными по виду их записи.

В зависимости от количества переменных, участвующих в записи неравенства различают неравенства с одной, двумя, тремя и большим числом переменных. Остановимся на них подробнее, а также приведем примеры неравенств с переменными.

Неравенства с одной переменной

Из названия понятно, что

Неравенством с одной переменной называют неравенство, в записи которого участвует одна переменная.

Например, x>3 – это неравенство с одной переменной x , 5≤y 3 +1 – неравенство с одной переменной y . Переменная в записи неравенства может встречаться несколько раз. Приведем примеры: (2·x−5·x 2 )·(x−1) и – это тоже неравенства с одной переменной.

Неравенства с двумя переменными

Неравенство, запись которого содержит две различные переменные, называется неравенством с двумя переменными.

В качестве примера неравенства с двумя переменными x и y приведем неравенство вида x 2 +3·y 2 >25 , а – это неравенство с двумя переменными p и q .

По виду записи на неравенства с двумя переменными похожи неравенства с параметром и одной переменной. Однако, в заданиях как правило сразу указывают, какие буквы являются параметрами, поэтому обычно не возникает вопросов о количестве переменных в неравенстве. Это же относится и к неравенствам с параметрами с тремя или большим количеством переменных.

Неравенства с тремя и большим числом переменных

Неравенства, в записи которых присутствуют три, четыре и т.д. переменные называют неравенствами с тремя, четырьмя и т.д. переменными соответственно.

Неравенства с тремя и большим числом переменных встречаются в школьном курсе математики не часто, но все же они имеют место. К примеру, шар с центром в начале координат, радиус которого равен 2 , можно задать неравенством с тремя переменными как x 2 +y 2 +z 2 ≤4 .

Решения неравенства: частное, общее и просто решение

От неравенств с переменными неотделимы их решения.

Решением неравенства с одной переменной называют такое значение переменной, которое обращает исходное неравенство в верное числовое неравенство.

Для примера рассмотрим неравенство с одной переменной вида x>7 . Возьмем x=10 . Подставив в исходное неравенство вместо переменной x ее значение 10 , получаем числовое неравенство 10>7 . Это верное числовое неравенство, поэтому 10 – это по определению решение неравенства x>7 . С другой стороны число 3 не является решением этого неравенства, так как подстановка этого значения вместо переменной x дает неверное числовое неравенство 3>7 .

Стоит обговорить вопрос о количестве решений конкретного неравенства с одной переменной. Заглядывая немного вперед, скажем, что неравенство с одной переменной может не иметь решений, иметь конечное число решений, или иметь бесконечно много решений. В этом Вы убедитесь, изучив процесс нахождения решений неравенств, который называют теми же словами, то есть, решением неравенств. Этот процесс имеет огромную практическую значимость, и с ним мы будем разбираться отдельно. А пока вернемся к теме нашей беседы.

• Неравенства могут не иметь ни одного решения, как, например, неравенство x 2 . Действительно, какое бы действительное число мы не подставили вместо переменной x , мы получим неверное неравенство, так как, изучив свойства степени, мы усвоили, что квадрат любого числа есть число неотрицательное, и оно не может быть меньше минус трех.
• Могут иметь единственное решение. Таковым, к примеру, является неравенство , имеющее решением x=1 , которое единственно.
• Могут иметь конечное число решений, к примеру, четыре или семь. В качестве примера приведем неравенство , оно имеет ровно два решения: 1 и −1 .
• А могут иметь и бесконечно много решений, как уже указанное выше неравенство x>7 . Его решением является любое действительное число, большее 7 , например, 11 , 65,32 или .

Все сказанное о количестве решений неравенств справедливо и для неравенств с двумя, тремя и большим количеством переменных.

Решением неравенства с двумя переменными называют пару значений этих переменных, при которых исходное неравенство обращается в верное числовое неравенство.

Для пояснения и примера возьмем неравенство с двумя переменными x и y вида x+1>2·y . Пара значений переменных x=1 , y=0 является решением данного неравенства, так как их подстановка дает верное числовое неравенство вида 1+1>2·0 . А вот пара x=2 , y=4 не является решением данного неравенства, так как их подстановка дает неверное числовое неравенство 2+1>2·4 .

Часто пары значений переменных записывают в скобках как координаты точек в прямоугольной декартовой системе координат на плоскости. Для предыдущего примера решение неравенства x+1>2·y , которое мы записали в виде x=1 , y=0 , можно записать как (1, 0) .

Аналогично определению решения неравенства с двумя переменными дается и определение решения неравенства с тремя и большим количеством переменных.

Решением неравенства с тремя, четырьмя и т.д. переменными называется тройка, четверка и т.д. значений этих переменных, которая обращает исходное неравенство в верное числовое неравенство.

В качестве примера решения неравенства с четырьмя переменными вида t 2 +x 2 +y 2 +z 2 ≤36 приведем четверку значений этих переменных t=1 , x=2 , y=3 , z=4 . Эта четверка чисел действительно является решением данного неравенства, так как 1 2 +2 2 +3 2 +4 2 ≤36 – верное числовое неравенство.

В заключение стоит обратить внимание на достаточно часто встречающиеся термины «частное решение неравенства» и «общее решение неравенства».

Под частным решением подразумевают какое-либо отдельно взятое решение данного неравенства.

Так 3 – это частное решение неравенства x . Другим частным решением данного неравенства является, например, число 2 . Можно указать и другие частные решения этого неравенства.

Общим решением неравенства называют множество всех частных решений этого неравенства.

Вернемся к предыдущему примеру x . Его общее решение – это множество всех действительных чисел, которые меньше пяти.

Однако намного чаще говорят просто «решение неравенства» без уточнения частное или общее. Ему обычно придают смысл общего решения. Например, если спрашивается «каково решение неравенства», то скорее всего интерес представляет все множество решений этого неравенства. А если интересует какое-то отдельно взятое решение (частное решение), то обычно и требуют указать одно из решений неравенства.

Как записать общее решение неравенства?

Умение записывать общее решение неравенств необходимо для записи ответа при решении неравенств. Поэтому не помешает детально разобраться с принятыми правилами записи. Начнем с принципов записи решений неравенств с одной переменной.

Из информации предыдущих пунктов понятно, что если неравенство с одной переменной имеет решение, то это или одно некоторое число, или некоторое множество чисел (конечное или бесконечное). То есть, общее решение неравенства с одной переменной – это некоторое числовое множество. Следовательно, и записывать его принято так же, как записываются числовые множества.

Например, если неравенство не имеет решений, то так и пишут «нет решений» или используют знак пустого множества ∅.

Когда общим решением неравенства является одно число, то его и так и записывают, к примеру, 0 , −7,2 или 7/9 , а иногда еще заключают в фигурные скобки.

Если решение неравенства представляется несколькими числами и их количество невелико, то их просто перечисляют через запятую (или через точку с запятой), или записывают через запятую в фигурных скобках. Например, если общее решение неравенства с одной переменной составляют три числа −5 , 1,5 и 47 , то записывают −5 , 1,5 , 47 или <−5, 1,5, 47>.

А для записи решений неравенств, имеющих бесконечное множество решений используют как принятые обозначения множеств натуральных, целых, рациональных, действительных чисел вида N , Z , Q и R , обозначения числовых промежутков и множеств отдельных чисел, простейшие неравенства, так и описание множества через характеристическое свойство, и все не названные способы. Но на практике наиболее часто пользуются простейшими неравенствами и числовыми промежутками. Например, если решением неравенства является число 1 , полуинтервал (3, 7] и луч [10, +∞) , то ответ можно записать как 1 , (3, 7] , [10, +∞) , или как 1∪(3, 7]∪ [10, +∞) , или как x=1 , 3 , x≥10 , или словами описать словами «единица, все числа большие трех, но меньшие или равные семи, а также все числа большие или равные десяти».

При записи общих решений неравенств с двумя, тремя и большим количеством переменных, если количество решений невелико, то их перечисляют все. Если же число частных решений велико или бесконечно, то обычно описывают множество значений, которые может принимать каждая переменная в отдельности. Например, неравенство с четырьмя переменными t , x , y и z может иметь такое решение: « t – любое целое число, x есть 0 или 1 , y=−5 , z=11 ».

Стоит заметить, что для неравенств с двумя переменными решение часто не описывают аналитически, а представляют в графическом виде, изображая множество решений неравенства на координатной плоскости. Например, решением неравенства 2·x−y≥5 является множество всех точек плоскости, лежащих на и ниже прямой, которой отвечает уравнение прямой с угловым коэффициентом y=2·x−5 . Изобразим их:

Иногда удобно графически представлять и решения неравенств с тремя переменными, в этом случае решение будет представлять собой некоторое множество точек трехмерного пространства.

Уроки математики и физики для школьников и родителей

четверг, 17 октября 2019 г.

Урок 14. Система неравенств с двумя переменными

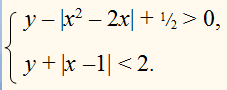
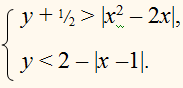
то из неравенств

у + 1 / ₂ ˃ | х 2 – 2 х | ,

следует, что

Целыми числами, удовлетворяющими этому неравенству, являются лишь 0 и 1 , поэтому система

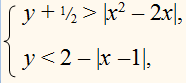
у = 0 и у = 1 .

1) Если у = 0 , то система примет следующий вид :

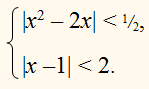
Проверка показывает, что первому неравенству удовлетворяют

лишь 0 и 2 . Следовательно, пары чисел

образуют решения исходной системы неравенств .

2) Если у = 1 , то система примет следующий вид :

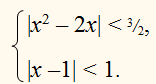
Графический метод решения систем неравенств с двумя переменными.

Суть метода решений системы неравенств с двумя переменными проста. Находим решение каждого неравенства в отдельности, изображаем решения на одной координатной плоскости и ищем пересечение этих решений.

Решить графически систему неравенство

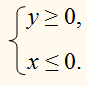
Сначала решим графически первое неравенство.

Затем второе .

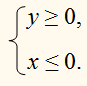
Решить графически систему неравенств :

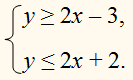
Сначала решим графически первое неравенство.

Затем второе .

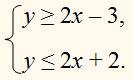
у = 2х – 3,

у = 2х + 2.

Решить систему неравенств :

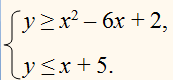
Найдём решение каждого неравенства в отдельности.

Для неравенства

множество всех точек расположено выше или “внутри” параболы.

Решения неравенства

у ≤ х + 5

расположены ниже прямой

у = х + 5 .

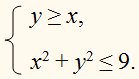
Изобразите на координатной плоскости множество решений системы неравенств :

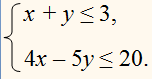
Построим прямые

4х – 5у = 20.

Множество решений первого неравенства показано горизонтальной штриховкой, а множество решений второго неравенства – вертикальной штриховкой.

Двойная штриховка – множество решений системы. Система задаёт плоский угол.

Изобразите на координатной плоскости множество решений системы неравенств :

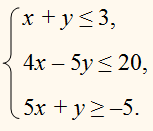
Построим прямые

4х – 5у = 20,

Этой системой задаётся треугольник.

Изобразите на координатной плоскости множество решений системы неравенств :

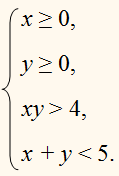
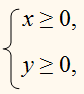
Геометрическим изображением решений неравенства

х + у или

является множество точек, лежащих ниже прямой, служащей графиком функции

у = 5 – х .

Геометрическим изображением решений неравенства ху ˃ 4, или, поскольку х ˃ 0 , неравенства

является множество точек, лежащих выше ветви гиперболы, служащей графиком функции

В итоге получаем множество точек координатной плоскости, лежащих в первом координатном углу ниже прямой, служащей графиком функции

у = 5 – х ,

и выше гиперболы, служащей графиком функции

Изобразить на координатной плоскости Оху фигуру Ф , координаты точек которой удовлетворяют системе неравенств :

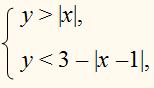
Построим графики функций

у = 3 – |х –1| ,

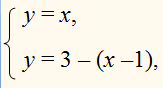
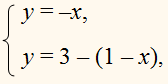
у = |х| и

у = 3 – |х –1| ,

лежащую в II квадранте.

Неравенству

удовлетворяют все точки координатной плоскости, расположенные выше графика функции

а неравенству

у |х –1|

все точки координатной плоскости, лежащие ниже графика функции

у = 3 – |х –1|.

Следовательно, исходной системе удовлетворяют все точки, лежащие внутри прямоугольника ОАСВ, полученного при пересечении графиков функций :

Алгебра

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Уравнения с двумя переменными

Порою в ур-нии содержится не одна, а две переменных. Такие ур-ния мы уже изучали в 7 классе. Приведем несколько примеров уравнений с двумя переменными:

В абсолютном большинстве таких задач для обозначения переменных используют буквы х и у. Решение указывают в виде пары чисел, причем на первом месте пишут значение х, а на втором – значение у. Например, несложно убедиться, что пара чисел (– 1; 3) является решением ур-ния

Для этого надо лишь вместо х подставить (– 1), а вместо у – число 3:

Получили верное равенство. Заметим, что пара (– 1; 3) является не единственным решением ур-ния. Например, пара (2; 0) также обращает ур-ние в верное рав-во:

У ур-ний с двумя неизвестными, как и у ур-ний с одной неизвестной, можно определить степень. Для этого надо представить их в таком виде, когда слева записан многочлен, а справа – ноль. Тогда степень ур-ния будет равна степени многочлена. Так как ур-ние содержит две переменных, то для обозначения такого многочлена используется запись Р(х; у).

Пример. Определите степень уравнения

Решение. Раскроем скобки слева, а потом перенесем все слагаемые в одну сторону:

х 3 + ху – х – 1 = 0

В левой части стоит многочлен третьей степени (подробнее об определении степени полинома можно узнать из этого урока). Поэтому и степень ур-ния равна 3.

График уравнения с двумя переменными

Очень часто ур-ние с 2 переменными имеет бесконечное число решений. Их удобно изображать в виде графика, ведь каждой паре чисел (х₁; у₁) соответствует точка на координатной плоскости с координатами х₁ и у₁.

Проще всего строить график уравнения с двумя переменными в том случае, когда удается выразить переменную у через х. Например, пусть надо построить график ур-ния

Выразим неизвестную величину у через х, то есть попытаемся получить ф-цию у = у(х):

Построим график ф-ции у = 3 – 2х. Он одновременно будет являться и графиком ур-ния 6х + 3у = 9:

Не всегда можно так преобразовать ур-ние, чтобы получилась ф-ция у = у(х). Действительно, по определению функции, каждому значению аргумента должно соответствовать только одно значение ф-ции. Однако рассмотрим пример ур-ния

Можно убедиться, что его обращают в верное рав-во пары чисел (1; 1) и (1; – 1):

Получается, что одному значению х(х = 1) соответствует сразу 2 значения у (у = 1 и у = –1). Это значит, что графиком такого ур-ния не может являться ф-ция у = у(х)

В данном случае возможно выразить х через у. Перенесем слагаемое у 2 вправо:

Получили «перевернутую ф-цию» х = х(у), где не у зависит от х, а х от у. Ф-ция является квадратичной, а потому ее графиком будет парабола:

Так как х и у в ф-ции поменялись местами, то ось параболы стала не вертикальной, а горизонтальной.

Встречаются случаи, когда из ур-ния невозможно получить ни ф-цию у(х), ни ф-цию х(у). Рассмотрим ур-ние

Его решениями являются пары чисел (0; 5) и (0; – 5). То есть значению х = 0 соответствует два значения у (5 и – 5), поэтому не получиться записать ф-цию у(х). С другой стороны, решениями ур-ния являются также пары (5; 0) и (– 5; 0), то есть значению у = 0 также соответствует два значения х (– 5 и 5), поэтому и записать ф-цию х(у) не удастся. Вообще данное ур-ние является частным случаем ур-ния

где R– некоторое постоянное число, или параметр. Оно называется уравнением окружности, потому что его графиком как раз и является окружность.

Докажем это утверждение. Пусть на координатной плоскости есть точка А с произвольными координатами (х; у):

Опустим из А перпендикуляр на ось Ох в точку В. Получили прямоугольный треугольник ОАВ. Его катет ОВ равен у, а катет АВ = х. По теореме Пифагора можно найти длину гипотенузы ОА, которая и является расстоянием от О до А:

ОА 2 = ОВ 2 + АВ 2 = х 2 + у 2

Окружность радиусом R– это множество точек, удаленных от центра на расстояние R. То есть расстояние ОА равно R, то точка А лежит на окружности радиусом R c центром в О:

х 2 + у 2 = ОА 2 = R 2

Таким образом, координаты любой точки, лежащей на расстоянии Rот центра, удовлетворяют ур-нию

В частности, графиком ур-ния

является окружность с радиусом 5 (так как 25 = 5 2 )

Система уравнений с двумя переменными

Рассмотрим задачу. Разность двух чисел равна единице, а сумма их квадратов составляет 25. Чему равны эти два числа?

В задаче неизвестны два числа. Поэтому обозначим их за неизвестные величины х и у. Первое условие задачи, «разность чисел равна 1», можно записать ур-нием:

Второе условие записывается так:

Нам надо найти такие х и у, которые удовлетворяют одновременно обоим условиям задачи. То есть необходимо решить систему уравнений с двумя переменными:

Напомним, что в 7 классе мы уже изучали сис-мы ур-ний, однако рассматривались только случаи, когда все они являлись линейными. В рассматриваемом случае второе ур-ние линейным НЕ является (потому что переменные величины стоят во второй степени).

Для каждого ур-ния построим отдельный график. Точки их пересечения и будут соответствовать решениям сис-мы. Ур-ниех 2 + у 2 = 25 задает окружность. Ур-ние х – у = 1 будет совпадать с графиком линейной ф-ции у = х – 1:

Графики пересеклись в двух точках: (4; 3) и (– 3; – 4). Подставив их в сис-му, можно убедиться, что именно эти пары чисел являются решениями этой сис-мы.

Конечно, графический метод решения сис-м не всегда точный. Однако он позволяет оценить количество корней и их примерное расположение. Также графики помогают при изучении сис-м, содержащих параметры.

Пример. Найдите с помощью графиков решение сис-мы ур-ний

Решение. Построим графики каждого ур-ния. График первого ур-ния представляет собой параболу, а второй график – это прямая у = 4 – х:

Видно, что графики пересеклись в двух точках: (– 1; 5) и (4; 0). Убедиться в точности построения можно, просто подставив эти значения в решаемую сис-му.

Пример. При каком а сис-ма ур-ний

имеет ровно 3 решения?

Решение. Преобразуем 2-ое ур-ние сис-мы:

График ур-ния х 2 + у 2 = 9 представляет собой окружность радиусом 3. График у = – х 2 + а является параболой с ветвями, смотрящими вниз. Покажем на плоскости различные варианты взаимного расположения этих графиков при различных значениях параметра а:

Видно, что 3 точки пересечения у параболы и окружности может быть только в случае, если вершина параболы касается окружности в точке (0; 3). Для этого парабола должна определяться ур-нием у = – х 2 + 3. Это значит, что только при значении а = 3 сис-ма имеет 3 решения.

Метод подстановки

Конечно, решать сис-му ур-ний графическим способом не очень удобно, так как часто можно получить лишь приближенный ответ. При изучении систем линейных уравнений с двумя переменными мы познакомились с двумя универсальными способами их решения: методы подстановки и сложения. К сожалению, для нелинейных сис-м нет универсальных методов их решения. Однако тот же способ подстановки иногда может помочь.

Его суть заключается в том, что в одном ур-нии надо выразить одну переменную через другую. В результате получится ф-ция у(х) или х(у), и ее можно будет подставить во второе ур-ние и тем самым получить ур-ние с одной неизвестной. Иногда такое действие называют исключением переменной.

Пример. Найдите решение сис-мы уравнений методом подстановки:

Решение. Сразу видно, что во втором ур-нии можно выразить у через х:

Подставим выражение у = х 2 – 6 в первое ур-ние:

2х 2 + х – 3у – 16 = 0

2х 2 + х – 3(х 2 – 6) – 16 = 0

Получилось ур-ние, в котором уже нет у! Его достаточно легко решить, ведь оно сводится к квадратному ур-нию:

2х 2 + х – 3(х 2 – 6) – 16 = 0

2х 2 + х – 3х 2 + 18 – 16 = 0

D = b 2 – 4ас = 1 2 – 4•(– 1)•2 = 1 + 8 = 9

Получили два возможных значения х. Теперь выполним обратную подстановку:

Итак, имеем две пары чисел, (– 1; – 5) и (2; – 2), которые являются решениями сис-мы ур-ний.

Ответ: (– 1; 5); (2; – 2)

Пример. При каких х и у справедлива сис-ма

Решение. Попробуем найти решение методом подстановки. Из второго ур-ния следует, что ни одна из переменных не равна нулю, ведь иначе бы произведение ху равнялось бы не 7, а нулю. Поэтому можно поделить второе ур-ние на х:

У нас получилось выразить у через х. Подставим полученное выражение в первое ур-ние:

Заменим переменную х 2 на t:

Умножим ур-ние на t. Так как х ≠ 0, то и t≠ 0,поэтому мы можем смело производить подобное умножение:

t 2 – 50t + 49 = 0

Получили квадратное ур-ние. Можно честно решить его, однако мы поступим проще. По теореме Виета, произведение корней ур-ния должно равняться 49 (свободный член ур-ния), а в сумме они должны давать 50 (второй коэффициент ур-ния с противоположным знаком). Под эти условия подходят числа 1 и 49:

На всякий случай подставим их в квадратное ур-ние и убедимся, что они действительно являются его корнями:

1 2 – 50•1 + 49 = 1 – 50 + 49 = 0

49 2 – 50•49 + 49 = 2401 – 2450 + 49 = 0

Итак, имеем два корня: t₁ = 1 и t₂ = 49.

Теперь произведем обратную замену:

х 2 = 1 или х 2 = 49

Имеем два квадратных ур-ния. Корнями первого являются числа

У ур-ния х 2 = 49 корни – это числа

Получили четыре значения х. Для каждого из них можно вычислить соответствующее значение у по формуле у = 7/х:

при х = –1; у = 7/ – 1 = – 7

при х = 1; у = 7/1 = 7

при х = – 7; у = 7/– 7 = – 1

при х = 7; у = 7/7 = 1

В итоге имеем 4 пары решений: (– 1; – 7), (1; 7), (– 7; – 1) и (7; 1).

Ответ: (– 1; – 7), (1; 7), (– 7; – 1), (7; 1).

Метод сложения

Очевидно, что не всегда в ур-нии можно выразить одну переменную через другую. Такую ситуацию можно, например, наблюдать в сис-ме

Однако здесь в каждом ур-нии есть слагаемое 6у 2 , взятое с разными знаками. За счет этого сис-му можно решить методом сложения, ведь при сложении левых частей ур-ний слагаемые 6у 2 и (– 6у 2 ) сократятся, что позволит исключить переменную у из ур-ния. Для этого надо сложить по отдельности левые и правые части ур-ний и получить новое ур-ние:

(3х 2 – 6у 2 + 3х) + (– 2х 2 + 6у 2 ) = –18 + 22

3х 2 – 6у 2 + 3х – 2х 2 + 6у 2 = 4

Получили ур-ние, не содержащее у. Его можно решить как обычное квадратное ур-ние:

D = b 2 – 4ас = 3 2 – 4•1•(– 4) = 9 + 16 = 25

Нашли два значения х. Подставляя его второе ур-ние, получим

– 2•(– 4) 2 + 6у 2 = 22

Имеем 4 решения сис-мы (– 4; 3), (– 4; – 3), (1; – 2), (1; 2).

Мы рассмотрели простейший случай использования метода сложения уравнений, когда ур-ния сис-мы можно сложить сразу. Однако порою их надо сначала умножить на какие-то числа, и лишь потом складывать.

Пример. Укажите решение для сис-мы:

Решение. Сразу складывать эти ур-ния нет смысла, потому что при этом не исчезнет ни одна переменная. Напомним, что обе части любого ур-ния можно умножить на число, не равное нулю, и в результате получится равносильное ур-ние. Поэтому второе ур-ние умножим на (– 2):– 4х 2 + 2у 2 = – 2

А вот теперь есть смысл сложить его с первым ур-нием, так как у них есть слагаемые 2у 2 с противоположными знаками:

(3х 2 – 2у 2 ) + (– 4х 2 + 2у 2 ) = 1 – 2

Полученные значения х будем подставлять в другое ур-ние, например, в 2х 2 – у 2 = 1 (на самом деле можно выбрать любое другое из ур-ний сис-мы).

Теперь подставим х = 1:

В итоге получаем 4 решения: (– 1; – 1), (– 1; 1), (1; – 1) и (1; 1)

Ответ:(– 1; – 1), (– 1; 1), (1; – 1), (1; 1).

Порою метод сложения и метод подстановки следует использовать одновременно.

Пример. Решите систему методом сложения:

Решение: постараемся избавиться от слагаемых с буквенной частью ху. Для этого умножим второе ур-ние на (– 2):

– 2х – 2у – 2ху = 12

Сложим его с первым ур-нием:

(3х + у + 2ху) + (– 2х – 2у – 2ху) = – 6 + 12

исключить переменную не удалось, однако мы получили линейное ур-ние. Выразим из него у:

Теперь можно подставить это выражение, например, во второе ур-ние системы:

х + (х – 6) + х(х – 6) = – 6

х = 0 или х – 4 = 0

Подставим полученные результаты в выражение у = х – 6

Получили два решения: (0; – 6) и (4; – 2).

Ответ: (0; – 6) и (4; – 2).

Разложение левой части уравнения на множители

Если нельзя использовать ни метод подстановки, ни способ сложения, то могут помочь другие методы. Например, иногда в одном ур-нии справа можно оставить ноль, а слева – разложить многочлен на множители.

Пример. Решите систему:

Решение. В верхнем ур-нии можно выполнить следующие преобразования:

9х 2 – у 2 = 3х – у

(3х – у)(3х + у) = (3х – у)

(3х – у)(3х + у) – (3х – у) = 0

Можно заметить, что в левой части находится разность двух выражений, содержащих множитель (3х – у). Этот множитель можно вынести за скобки, при этом вместо второго выражения останется только единица, ведь его можно переписать как (3х – у)•1 (при умножении на единицу любое выр-ние остается неизменным):

(3х – у)(3х + у) – (3х – у)•1 = 0

(3х – у)(3х + у – 1) = 0

Вспомним, что произведение равно нулю, если один из его сомножителей нулевой. Поэтому

3х – у = 0 или 3х + у – 1 = 0

у = 3х или у = 1 – 3х

Получили два возможных варианта выражения для у. Будем подставлять их во второе ур-ние:

х = 0 или – 2х + 3 = 0

Найдем значение у, учитывая, что у = 3х:

Имеем решения (0; 0) и (1,5; 4,5). Далее рассмотрим второй случай, когда у = 1 – 3х:

х 2 + (1 – 3х) = х(1 – 3х)

х 2 + 1 – 3х = х – 3х 2

Перенося слагаемые влево, получаем квадратное ур-ние:

х 2 + 1 – 3х – х + 3х 2 = 0

D = b 2 – 4ас = (– 4) 2 – 4•4•1 = 0

Получаем, что у квадратного ур-ния есть лишь один корень:

Найдем соответствующее ему значение у:

Получили третье решение: (0,5; – 0,5).

Ответ: (0; 0); (1,5; 4,5);(0,5; – 0,5).

Системы ур-ний часто используются при решении геометрических задач.

Пример. Площадь прямоугольного треугольника равна 150 см 2 . Известно, что один из его катетов больше другого на 5 см. Каков периметр треугольника?

Решение. Традиционно катеты обозначают буквами а и b. Площадь прямоугольного треугольника равна половине произведения катетов:

Отсюда следует ур-ние:

Будем считать, что катет а больше, чем b. Тогда из условия можно записать

Итак, получается система:

Очевидно, что систему можно решить подстановкой а = 5 + b

b 2 + 5b – 300 = 0

Решая это квадратное ур-ние, легко получить два значения b: 20 и (– 15). По смыслу задачи длина катета должна измеряться положительным числом, а потому b = 20. Второй катет на 5 см меньше, то есть он равен 20 – 5 = 15 см. Длину гипотенузы с можно найти по теореме Пифагора:

с 2 = а 2 + b 2 = 20 2 + 15 2 = 625

Периметр треугольника – это сумма его сторон, она равна 25 + 20 + 15 = 60 см.

Линейное неравенство с двумя переменными

Изучение неравенств с двумя переменными начнем с простейших из них – линейных неравенств. Их можно получить из линейных ур-ний, поставив вместо знака «=» один из четырех знаков сравнения.

Приведем примеры линейных неравенств с двумя переменными:

– 18,4x + 45,325y + 54,36 0

Пример. Отметьте на координатной прямой все решения неравенства с двумя переменными

Решение. Рассмотрим ур-ние

Перенеся часть слагаемых вправо, можно получить функцию

Построим ее график. Он представляет собой параболу, которая разбивает плоскость на две области:

Для определения того, выполняется ли нер-во в той или иной области, достаточно рассмотреть по одной точке в каждой из областей. Начнем с внутренней области. К ней относится начало координат, точка (0; 0). Подставив х = 0 и у = 0 в нер-во, мы увидим, что оно выполняется:

Во второй области выполняется обратное нер-во у – х 2 + 5 2 + 5 4 + 2х 2 у + у 2 > 0

Решение. Изучим ур-ние

х 4 + 2х 2 у + у 2 = 0

В левой части стоит квадрат суммы слагаемых х 2 и у:

(х 2 + у) 2 = (х 2 ) 2 + 2х 2 у + у 2 = х 4 + 2х 2 у + у 2

С учетом этого ур-ние можно переписать так:

Построим график и определим, какое нер-во выполняется в полученных областях. В области I возьмем точку (0; – 1). При ее подстановке в исходное нер-во получаем:

0 4 + 2•0 2 (– 1) + (– 1) 2 > 0

Однако и в области II выполняется то же самое нер-во. Это можно увидеть на примере точки (0; 1):

0 4 + 2•0 2 •1 + 1 2 > 0

Получается, что решениями нер-ва являются точки обеих областей. То есть надо заштриховать всю координатную плоскость, кроме самой кривой у = – х 2 , которую мы покажем из-за этого штрихпунктирной линией:

Отдельно отметим, что возможны случаи, когда график ур-ния разбивает плоскость не на две, а на большее кол-во областей. В качестве примера можно привести нер-во

Ему соответствует ур-ние ху – 5 = 0

Из него можно получить функцию у = 5/х, графиком которой является гипербола. Этот график образует 3 области. Будем действовать как и раньше – выберем из каждой области по одной точке и посмотрим, выполняется ли на нем нер-во ух – 5 > 0. Из области I возьмем точку (– 5; – 5):

ху – 5 = (– 5)•(– 5) – 5 = 25 – 5 > 0

Из II области выберем точку (5; 5):

ху – 5 = 5•5 – 5 = 20 > 0

Наконец, из III области возьмем точку (0; 0):

ху – 5 = 0•0 – 5 = 0 – 5 2 + у 2 = 9 является окружность радиусом 3, то решением первого нер-ва является круг:

Нер-во х – у > 0 является линейным. Его решением будет полуплоскость:

Теперь совместим два полученных решения. Решением системы нер-в будет пересечение заштрихованных областей. Ведь именно здесь оба нер-ва системы будут выполняться одновременно. Это пересечение представляет собой полукруг (он заштрихован квадратиками):

Пример. Постройте решение системы нер-в

Решение. Построим графики ур-ний х 2 – у = 2 и у 2 – х = 2. Первый из них будет являться параболой у = х 2 – 2. Второй же будет выглядеть, как парабола, повернутая на 90°. Это будет функция х = у 2 – 2:

В том, что мы выбрали правильную область на плоскости, можно убедиться, просто подставив одну из ее точек, в частности (0; 0), в систему:

Урок.”Неравенства с двумя переменными.”
методическая разработка по алгебре (9 класс) на тему

9 класс. Тема урока:”Неравенства с двумя переменными.” Объяснение нового материала.

Скачать:

Вложение	Размер
urok_1_neravenstva_s_dvumya_peremennymi.docx	210.89 КБ

Предварительный просмотр:

Тема: Неравенства с двумя переменными.

Учебная задача. Формирование системы фактов «неравенства с двумя переменными», «линейные неравенства».

дидактическая: ввести понятие неравенства с двумя переменными и его решения; формировать умение решать линейные неравенства с двумя переменными..

психологическая: формирование видов учебно-познавательной деятельности;

воспитательная: проверка грамотной устной и письменной математической речи учащихся.

I.Организационный момент. Сообщение темы и цели урока.

Девиз нашего урока:

«Знание собирается по капле »

II. этап. Устно- письменный опрос учащихся с целью установления содержательных связей между ведущими линиями школьного курса математики.

1. Какие из следующих чисел: –2; –1; 0; 2; 3 – являются решением неравенства х 3 – 2х ≥ 1?

2. Подберите два каких-нибудь числа разных знаков, чтобы их сумма была больше 5.

Контроль усвоения материала(самостоятельная работа).

1.Сумма двух чисел равна 30, а их произведение равно 216. Найдите эти числа.

2. Гипотенуза прямоугольного треугольника равна 20 см, а его периметр равен 48 см. Найдите катеты треугольника.

1.Сумма двух чисел равна 40, а их произведение равно 364. Найдите эти числа.

2. Гипотенуза прямоугольного треугольника равна 25 см, а его периметр равен 60 см. Найдите катеты треугольника.

III. Объяснение нового материала.

1. Понятие неравенства с двумя переменными и его решения.

2. Линейное неравенство с двумя переменными.

Рассмотрим неравенства: 0,5х 2 -2у+l 20 -неравенство с двумя переменными.

Рассмотрим неравенство 0,5х 2 -2у+l

При х=1, у=2. Получим верное неравенство 0,5 • 1 – 2 • 2 + 1

Пару чисел (1; 2), в которой на первом месте — значение х, а на втором — значение у, называют решением неравенства 0,5х 2 -2у+l

Определение. Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.

Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой. Говорят, что эта фигура задается или описывается неравенством.

Рассмотрим линейные неравенства с двумя переменными.

Определение. Линейным неравенством с двумя переменными называется неравенство вида ах + by с, где х и у — переменные, а, b и с – некоторые числа.

Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение. Графиком линейного уравнения ах + by = с, в котором а или b не равно нулю, является прямая линия. Она разбивает множество не принадлежащих ей точек координатной плоскости на две области, представляющие открытые полуплоскости.

На примерах рассмотрим, как изображается множество решений неравенства с двумя переменными на координатной плоскости.

Пример 1. Изобразим на координатной плоскости множество решений неравенства 2у+3х≤6.

Строим прямую 2у+3х=6, у=3-1,5х

Прямая разбивает множество всех точек координатной плоскости на точки, расположенные ниже ее, и точки, расположенные выше ее. Возьмем из каждой области по контрольной точке: А(1;1), В(1;3).

Координаты точки А удовлетворяют данному неравенству 2у+3х≤6, 2·1+3·1≤6, 5≤6

Координаты точки В не удовлетворяют данному неравенству 2у+3х≤6, 2·3+3·1≤6.

Данное неравенство может изменить знак на прямой 2у+3х=6, то неравенству удовлетворяет множество точек той области, где расположена точка А. Заштрихуем эту область. Мы изобразили множество решений неравенства 2у+3х≤6.

Пример 2. Покажем штриховкой на координатной плоскости график неравенства 2х + Зу

Начертим график уравнения 2х + Зу = 6 . Пара (0; 0) является решением неравенства 2х + Зу

Пример 3. Изобразим на координатной плоскости множество решений неравенства 2х – Зу ≤-6.

Начертим график уравнения 2х-Зу = -6 . Отметим в какой-нибудь полуплоскости точку, например, точку (1; 1). Пара (1; 1) не является решением неравенства 2х – Зу ≤-6. Точка с координатами (1; 1) лежит в нижней полуплоскости. Значит, графиком неравенства является верхняя полуплоскость вместе с прямой 2х – Зу = -6.

Для изображения множества решений неравенства на координатной плоскости поступают следующим образом:

1. Строим график функции y = f(x), который разбивает плоскость на две области.

2. Выбираем любую из полученных областей и рассматриваем в ней произвольную точку. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.

3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают в множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией.

Вывод: – решением неравенства f(x,y)˃0, [f(x,y)

-графиком неравенства с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х, у), где каждая пара (х,у) является решением данного неравенства.

Графики некоторых неравенств.

IV. Формирование умений и навыков.

3. Изобразите на координатной плоскости множество точек, задаваемое неравенством:

Произведение двух чисел является неотрицательным в том случае, если эти числа имеют одинаковые знаки. Значит, когда

Первой системе соответствует первая координатная четверть, а другой системе – третья координатная четверть. Множеством решений неравенства-объединение первой и третьей координатных четвертей, включая оси координат.

Сильным в учебе учащимся можно предложить дополнительно выполнить № 556.

Построим график уравнения | у | = 1 – | х |. Для этого нужно раскрыть знаки модуля.

Получим четыре случая:

1) х ≥ 0, у ≥ 0; у = 1 – х.

Объединяя все эти случаи, получим фигуру:

Данному неравенству удовлетворяет множество точек внутренней области этой фигуры.

V. 4 этап . Оценочно -рефлексивный .

Подведение итогов урока, комментарии по домашнему заданию. Обратить внимание учащихся на теоретические факты, которые вспомнили на уроке, о необходимости их выучить.

– Что называется решением неравенства с двумя переменными?

– Сколько решений может иметь неравенство с двумя переменными?

– Как найти множество решений линейного неравенства с двумя переменными?

Домашнее задание: № 483 (б, г), № 484 (б, в), № 486.

Д о п о л н и т е л ь н о: № 492 (б).

«Решение задач с помощью систем уравнений второй степени.»

1.Найдите два натуральных числа, сумма которых равна 7, а произведение 12.

2.Площадь прямоугольного участка равна 120см 2 , а периметр равен 46см. Найдите ширину и длину участка.

3.Гипотенуза прямоугольного треугольника равна65, а разность катетов треугольника равна 23. Найдите площадь треугольника.

1.Найдите два натуральных числа, сумма которых равна 9, а произведение 18.

2.Площадь прямоугольного участка равна 90см 2 , а периметр равен 46см. Найдите ширину и длину участка.

3.Гипотенуза прямоугольного треугольника равна 73, а разность катетов треугольника равна 7. Найдите площадь треугольника.

1.Найдите два натуральных числа, сумма которых равна 9, а произведение 14.

2.Площадь прямоугольного участка равна 80см 2 , а периметр равен 42см. Найдите ширину и длину участка.

3.Гипотенуза прямоугольного треугольника равна 106, а разность катетов треугольника равна 34. Найдите площадь треугольника.

1.Найдите два натуральных числа, сумма которых равна 11, а произведение 30.

2.Площадь прямоугольного участка равна 98см 2 , а периметр равен 42см. найдите ширину и длину участка.

3.Гипотенуза прямоугольного треугольника равна 89, а разность катетов треугольника равна 41. Найдите площадь треугольника.