Числовые выражения – формулы, примеры и алгоритм решения в 7 классе

Выражения и их преобразования

☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: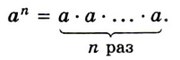
Степенью числа а с показателем 1 называют само число а: а 1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.

☑ 2. Свойства степеней с натуральными показателями:

а m • а n = а m+n

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

а m : а n = а m- n , где а ≠ 0, m ≥ n

(а m ) n = а mn

При возведении степени в степень основание оставляют прежним, а показатели перемножают.

(ab) n = а n b n

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а 2 х, –3а 2 b 3 , 4, х, у 5 — одночлены.

Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.

☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,

(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,

(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,

а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,

(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2

☑ 6. Формулы сокращённого умножения:

(а + b) 2 = а 2 + 2аb + b 2

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а – b) 2 = а 2 – 2аb + b 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(а – b)(а + b) = а 2 – b 2

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

а 3 + b 3 = (а + b)(a 2 – аb + b 2 )

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

а 3 – b 3 = (а – b)(a 2 + ab + b 2 )

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.

Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :

5х 3 – х 2 у = х 2 (5х – у) .

Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:

3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).

Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:

а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).

Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.

Алгебра 7 класс Все формулы

Уравнения

☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x + 1 = 5х – 15 , так как верно равенство 3 • 8 + 1 = 5 • 8 – 15 .

Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.

☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.

При решении уравнений с одной переменной используются следующие свойства:

если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b , где х — переменная, а и b — числа.

Если а ≠ 0 , то уравнение ах = b имеет единственный корень b/a .

Например, уравнение 7х = 2 имеет корень 2/7 .

Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.

Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.

☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = -1, у = 4 — решение уравнения 5х + 3у = 7 .

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.

☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.

☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.

☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.

При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:

если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.

При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

выражают из какого–либо уравнения системы одну переменную через другую;
подставляют в другое уравнение системы вместо этой переменной полученное выражение;
решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

Алгебра 7 класс Все формулы

Функции

☑ 16. Функциональная зависимость , или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b , где х — независимая переменная, k и b — числа.

Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.

Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b , параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.

Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.

Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.

График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.

График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.

Статистические характеристики

☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.

Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.

Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.

Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.

Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.

Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.

Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:

Числовые выражения. 7-й класс

Класс: 7

Презентация к уроку

Цели урока:

Повторить и углубить умение учащихся находить значения числовых выражений, составленных из рациональных чисел с помощью знаков сложения, вычитания, умножения и деления;
Учащиеся должны знать, что выражение, содержащее действие деление на нуль, не имеет смысла.
Развить познавательный интерес учащихся к изучению нового предмета.
Развить мышление, память, речь, совершенствовать вычислительные навыки учащихся, умение работать в оптимальном темпе.

Оборудование: ПК, мультимедийная установка; карточки с домашнем заданием (Приложение 1)

Тип урока: урок повторения и обобщения знаний полученных в курсе математики 5-6 классов.

Формы работы: фронтальная, коллективная, самостоятельная работа.

Ход урока

1. Организационный момент (2-4 минуты)

Поздравить учащихся с началом нового учебного года.

***
И снова в позолоте тополя,
А школа – как корабль у причала,
Где ждут учеников учителя,
Чтоб новой жизни положить начало.

***
Пусть счастье в дверь твою стучит,
Открой ее скорей пошире.
Путь жизни тайною покрыт,
Но так прекрасно в этом мире!
И пусть всегда – в окошке свет,
Улыбка мамина – с порога.
Пусть будет много добрых лет
И в жизни легкая дорога!

***
Осенние мотивы
Эта шикарная женщина ОСЕНЬ
Себя подарила беспутному ветру,
И что он ни скажет, и что ни попросит,
Ему отдавала, не чувствуя меры.
Листвы разноцветной большие охапки
Бросала к ногам его брачным букетом,
И буйные краски, и солнца остатки,
И слезы дождей, и туман пред рассветом.
А ветер беспутный шаталец по свету,
Любя самого лишь себя, свою прихоть,
И даже шикарную женщину эту
Старался как можно больнее обидеть,
Сорвать с нее платье нахальным порывом,
Чтоб голая так до зимы простояла…
А ОСЕНЬ прощала, лишь с тихим надрывом
Уже обреченные слезы роняла.
В зимовьих объятьях она умирает,
И проседь теперь в волосах, а не просинь.
Под снежной накидкой никто не узнает
Эту шикарную женщину – ОСЕНЬ.

2. Что изучает алгебра?

У.: Какой предмет мы изучали в прошлом году?

Ученики: Математику.

У.:

Есть о математике молва,
Что она в порядок ум приводит.
Поэтому хорошие слова
Часто говорят о ней в народе.

У.: Чем мы занимались на уроках математики?

Ученики: Проводили вычисления с целыми и дробными числами, решали уравнения, задачи, строили фигуры в координатной плоскости.

У.: Все это составляло содержание предмета «Математика». Этот предмет подразделяется на огромное число самостоятельных дисциплин: алгебра, геометрию, теорию вероятностей, математический анализ, теорию игр и т. д. Мы приступаем к изучению алгебры. Вы уже дома познакомились с учебником. Чем он отличается, например, от учебника литературы?

Ученики: В нем много цифр и букв, причем букв латинских.

У.: Мы с вами помним, что буквы нам помогают записывать свойства действий над числами в удобной для запоминания форме. Говорят: «Высказанное утверждение записано на математическом языке». Например, переместительное свойство умножения: от перестановки множителей произведение не меняется (a · b = b · a ). Вспомните, как найти расстояние, зная время и скорость.

Ученики: Чтобы найти расстояние, надо время умножить на скорость.

У.: Записываем это короче: s = v · t. То есть буквы помогают записывать в виде формул правила для нахождения значений интересующих нас величин. Чем еще алгебра отличается, например, от арифметики? В арифметических задачах по известным правилам находят неизвестное число. В алгебре неизвестную величину обозначают буквой. Эта неизвестная величина и данные в условии задачи связываются между собой уравнением, из решения которого и находится неизвестная величина. Отдельные алгебраические понятия и приемы решения задач возникли несколько тысяч лет назад в древних государствах – Вавилоне и Египте. О состоянии математических знаний в те века можно судить по древним рукописям (папирусам), найденным на местах древних городов.

Около 4000 лет назад в Вавилоне и в Египте ученые уже умели составлять линейные уравнения, с помощью которых они решали самые разнообразные задачи землемерия, строительного искусства и военного дела. Например, в Британском музее хранится задача из папируса Ринда (его называли также папирусом Ахмеса), относящегося к периоду 2000 – 1700 гг. до н. э.: «Найти число, если известно, что от прибавления к нему 2/3 его и вычитания от полученной суммы ее трети получается число 10». Решение этой задачи сводится к решению линейного уравнения:

В VII в. до н. э. греки усвоили достижения египтян в математике. В начале IX в. (830 год) хорезмийский ученый Мухаммед-бен-Муса ал-Хорезми написал книгу «Хисаб аль джабр вал-Мукабала» («Метод восстановления и противопоставления») – это была первая книга по алгебре. Она имеет особое значение в истории математики как руководство, по которому долгое время обучалась вся Европа. В ней он впервые рассмотрел методы и приемы алгебры.

Ал-джебр
(перенос слагаемых)

При решении уравненья,
Если в части одной,
Безразлично какой,
Встретится член отрицательный,
Мы к обеим частям,
С этим членом сличив.
Равный член придадим,
Только с знаком другим,—
И найдем результат, нам желательный!

Вал-мукабала
(приведение подобных)

Дальше смотрим в уравненье,
Можно ль сделать приведенье,
Если члены есть подобны,
Сопоставить их удобно.
Вычитая равный член из них,
К одному приводим их.

С момента написания этой книги алгебра становится самостоятельной наукой. Само слово «алгебра» произошло, вероятно, от слова «ал джебр», что означает «восстановление». Словом «алгебра» в арабском языке называлось искусство врача восстанавливать сломанную руку или ногу. Хирурга у арабов называли алгебраистом. Таким образом, математика позаимствовала это слово из медицины.

Дальнейшее развитие алгебры происходило в основном в Индии (до XII в.) и в Средней Азии (до XV в.). Алгебру до XVII в. условно называли риторической (словесной). Дело в том, что тогда не существовало единых условных знаков «+», «-», «а 2 » и многих других которые используем мы. Условие задачи, все действия и ответ записывали полностью словами. Для удобства запоминания иногда эта запись делалась в стихах. Математические символы вводились постепенно. Так знак равенства «=» введен английским ученым Р. Рикордом в 1557 г., знаки «:» и «*» – немецким математиком Лейбницем в конце XVII в. , скобки – XVI в. Математические символы дали возможность ученым разных стран понять друг друга. В формировании алгебры как науки большие заслуги принадлежат французским ученым Франсуа Виету и Рене Декарту. В течение XVIII-XX в. из алгебры выросли новые математические науки: алгебра многочленов, векторная алгебра. Науки эти изучаются в высшей школе.

В школьной алгебре задачи решают путем составления уравнений, изучают сами уравнения, связи между величинами (некоторые из этих связей называются функциями). При этом используются буквы, выражения с буквами подвергаются различным преобразованиям (тождественным преобразованиям). Но за всеми этими буквами чаще всего скрываются числа.

Иногда говорят: «Алгебра держится на четырех китах: на уравнении, числе, тождестве, функции».Алгебра, к изучению которой мы приступаем, дает человеку возможность не только выполнять различные вычисления, но и учит его делать это как можно быстрее, рациональнее.

3. Устные упражнения.

1. Найдите сумму чисел -3,7 и 6,7 (отв. 3); найдите произведение чисел найдите разность чисел Повторить правила выполнения арифметических действий с обыкновенными дробями и рациональными числами.

2. Я задумал три числа. Найдите первое, если известно, что число, противоположное ему, равно 6. Найдите второе, если число обратное ему равно 3. Найдите третье, если известно, что, умножив его на

4. Изучение новой темы.

При решении многих задач приходится над заданными числами производить арифметические действия: сложение, вычитание, умножение и деление. Но часто, прежде чем доводить до конца каждое из этих действий, удобно заранее указать порядок (план), следуя которому надо производить эти действия. Этот план сводится к тому, что по данным задачи с помощью чисел, знаков действий и скобок составляется числовое выражение.

Примеры:

Если в числовом выражении выполнить все указанные в нем действия, то в результате получим число, про которое говорят, что оно равно данному числовому выражению.

Так первое числовое выражение равно 2, второе равно тоже 2, третье же равно 0.

Определение 1: Запись, составленная из чисел с помощью арифметических действий (сложение, вычитание, умножение, деление, возведение в степень) называет числовым (арифметическим) выражением.

Числовое выражение может состоять из одного числа.

Определение 2: Значением числового выражения называется число, полученное в результате выполнения указанных в числовом выражении действий.

Примеры: Поезд двигался сначала 50 минут со скоростью шестьдесят километров в час, затем остановился на станции на десять минут, потом двигался еще один час со скоростью 40 км/ч. Найдите среднюю скорость движения поезда.

Решение: По определению средней скорости движения она равна отношению пройденного пути к затраченному на этот путь времени. Вычислим путь и время движения. Прежде всего учтем, что (перешли к одинаковым единицам измерения времени). В начале движения был пройден путь в конце – путь 40·1(км).

Общий пройденный путь описывается числовым выражением:

Время, затраченное на этот путь (включая время, затраченное на остановку), описывается числовым выражением: Тогда средняя скорость движения описывается выражением: Если вычислить это выражение, то получим: .

Определение 3: Два числовых выражения, соединенные знаком «=», образуют числовое равенство. Если значения левой и правой частей числового равенства совпадают, то равенство называют верным, в противном случае – неверным.

Примеры: – верное числовое равенство;

6 + 12 · 3 = (6 + 12) · 3 – неверное числовое равенство, так как 42 ≠54.

Скобки помогают установить порядок действий. При этом предполагается, что все действия возможно осуществить. Всегда возможно произвести сложение, вычитание и умножение любых чисел. А вот делить одно число на другое можно, только если делитель не равен нулю: на нуль делить нельзя. Если в данном выражении на некотором этапе вычислений требуется делить на нуль, то это выражение не имеет смысла.

Примеры: Эти выражения не имеют смысла.

Повторить порядок выполнения действий в числовом выражении. Повторить правила выполнения действий с дробями.

5. Закрепление изученного материала.

Пр. №1 Установите, какие из следующих выражений имеют смысл и какие не имеют. Для имеющих смысл найдите числа, которым они равны.

Пр. №2 Записать в виде равенства и проверить, верно ли оно:

а) 20% от числа 240 равны 62 (240 · 0,2 = 62 не верно);

б) число 18 составляет 3% от числа 600 (18 = 0,03 · 600 не верно);

в) произведение чисел и 5 составляет 11% от числа 700 верно;

г) четвертая часть числа 18 равна 5% от числа 90 верно;

д) число 111:3 равно 10% от числа 370 (111 : 3 = 0,1 · 370, верно);

е) 650% от числа 12 равны 77 (6,5 · 12 = 77 78 ≠ 77, не верно).

6. Домашнее задание: конспект, 10 (А)

7. Подведение итогов урока

Литература:

Математика № 12, 2004 год
Алгебра: 7 класс. Контрольные, самостоятельные, рейтинговые работы/ В. А. Гольдич. – М.: Эксмо, 2008. – 144 с. – (Мастер-класс для учителя).
Интернет ресурсы.

Числовые выражения — формулы, примеры и алгоритм решения в 7 классе

Основой математики являются числовые выражения. В 7 классе они изучаются подробнее, поскольку к ним применяются специальные методики, позволяющие выполнять операции упрощения. Последние используются для оптимизации вычислений при решении задач по различным дисциплинам с физико-математическим уклоном. Однако специалисты рекомендуют изучить теорию, которая поможет избежать множества ошибок при расчетах величин.

Общие сведения

Многие начинающие математики часто путают два понятия: числовые и алгебраические выражения. Между ними существует разница, которая заключается в определениях. Числовое выражение — вид математического тождества, состоящего только из чисел, скобок и знаков арифметических операций. Например, тождество «5+8/3−4*2» является числовым выражением. Оно означает последовательность математических знаков, объединенных в одну логическую цепочку.

Алгебраическим называется совокупность переменных и числовых выражений, имеющих логическое завершение. Объяснение смысла логики выражения имеет такой вид: совокупность чисел и переменных, связанных между собой арифметическими операциями умножения, деления, сложения и вычитания. Например, выражение «5t-2/3» — алгебраическое, поскольку в нем присутствует переменная «t».

Математическим выражением не является набор символов, не имеющий логического завершения. Например, 234±4678++* — обыкновенный ряд, который можно составить из цифр и знаков арифметических операций. Последние имеют следующие обозначения:

* — произведение.

/ — деление.

+ — сложение.

— — вычитание.
Произведение — вид арифметической операции, позволяющей умножить одну величину на другую. Она состоит из трех основных элементов. К ним относятся: I множитель, II множитель и произведение (результат). Математики утверждают, что для сокращения сложения применяется умножение, то есть 3+3+3+3+3+3=3*6=18. Если рассчитать оба выражения, то они будут равными между собой.
Деление — арифметическая операция, используемая для поиска сомножителей искомого числа. Она состоит из следующих обязательных компонентов: делимого, делителя и частного. Первый элемент — составное значение, второй — один из множителей первого, а частное — результат операции деления.
Сложение — простейшая арифметическая операция, составление которой осуществляется минимум из трех элементов и позволяющая увеличивать искомую величину на определенное значение. Компоненты имеют следующие названия: два слагаемых и результат, который называется суммой.
Вычитание — операция, необходимая для уменьшения искомого числа на заданную величину. Она состоит из трех компонентов: уменьшаемого, вычитаемого и разности. Первое — числовое значение, от которого отнимается вычитаемое.
Однако у каждой операции есть определенный приоритет.
Приоритет операций
При вычислении математических выражений существует определенный приоритет арифметических операций. Сначала выполняются умножение и деление. Они обладают максимальной величиной приоритета. Иногда для оптимизации вычислений можно выполнять действие над числами или переменными в любой последовательности, то есть пример «2*26/13» можно решить двумя способами:

(2*26)/13=52/13=4.

2*(26/13)=4.
В первом случае операция займет больше ресурсов: сначала требуется 2 умножить на 26, высчитать результат, а затем его поделить на 13. Это не слишком удобно. Однако для оптимизации вычислений рекомендуется применять второй способ, поскольку особого труда не составляет 26 разделить на 13, а затем результат перемножить с двойкой.
Сложение и вычитание имеют также одинаковый уровень приоритета. Можно сначала для удобства выполнить сложение, а затем вычитание или наоборот. Специалисты рекомендуют руководствоваться важным принципом: вычисления должны быть максимально упрощены. Чтобы задать приоритет какому-либо математическому действию, необходимо взять часть выражения в скобки (сгруппировать). В результате этого первой будет выполняться операция, находящаяся в скобках.
Для примера нужно найти значение выражения: 2*2−2 (3−2)*7/14−25/5. Решать его правильно по такой методике с учетом приоритета:

3−2=1.

1*2*7/14=1.

2*2=4.

25/5=5.

4−1−5=2.
Если не учитывать приоритет выполнения операций, то найти значение числового выражения можно по такой схеме:

2*2=4.

4−2=2.

2*1=2.

2*7/14=1.

1−25=24.

24/5=4,8.
Если сравнить два результата, то они не совпадают. На основании этого можно сделать вывод, что приоритет имеет значение при выполнении вычислений и нарушать его нельзя, поскольку исчезнет логика выражения. Однако не только скобки позволяют установить очередность операций. Существуют некоторые исключения.
Частные случаи или исключения
В алгебре, как и во всех дисциплинах с физико-математическим уклоном, учитывается скорость вычислений. Это существенно влияет на время выполнения какого-либо задания. В некоторых случаях выражение можно упростить, используя формулы сокращенного умножения и выполняя математические преобразования с элементами тождества. Для этих целей рекомендуется пользоваться соответствующими правилами:

Если выражение представлено в виде дробного рационального тождества, то следует вынести общий множитель, а затем сократить на него.

Необходимо применять формулы сокращенного умножения.

Раскрытие скобок и приведение подобных компонентов выполняется в том случае, когда в этом есть необходимость.

Числовое выражение необходимо вычислять, а алгебраическое — приводить к простой форме.
Следует отметить, что в первом случае обязательно требуется проверить равенство знаменателя нулевому значению. Для этого следует указать величину переменной, которая не должна превращать знаменатель в 0.
Методика вычисления
Математики разработали специальную методику нахождения значения выражения. Она сводится к разбиению числового выражения на части. Этот подход впервые использовал Пифагор. Суть его состоит в следующем:

Разбить тождество на части, обозначив каждую из них определенной литерой.

Найти величину каждого компонента.

Вычислить окончательный результат.
Для демонстрации алгоритма необходимо решить пример: 9*7−21 (74/(43+31))/7−64-(27−3*9). Практическая реализация методики имеет следующий вид:

Разбить тождество по частям: K=9*7, L=(74/(43+31))/7, M=21, N=64, O=27−3*9.

Записать в полной форме с учетом замен: K-L*M-N-O.

Вычислить первый элемент: К=63.

Найти II компонент: L=1/7.

Рассчитать III и II: 21/7=3.

Найти О: О=0.

Определить результат, подставив в выражение замен найденные величины: 63−3−64−0=-4.
Следует отметить, что этот алгоритм позволяет реализовать принцип «дробления» задания на несколько компонентов. Разбивать тождество можно в произвольном порядке.
Таким образом, для расчета значения числового выражения нужно воспользоваться специальным алгоритмом, который позволит существенно оптимизировать вычисления.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки ” + ” , ” · ” , ” – ” , ” ÷ ” , то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14 – 2 · 15 ÷ 6 – 3 .
Выполним сначала умножение и деление. Получаем:
14 – 2 · 15 ÷ 6 – 3 = 14 – 30 ÷ 6 – 3 = 14 – 5 – 3 .
Теперь проводим вычитание и получаем окончательный результат:
14 – 5 – 3 = 9 – 3 = 6 .
Вычислим: 0 , 5 – 2 · – 7 + 2 3 ÷ 2 3 4 · 11 12 .
Сначала выполняем преобразование дробей, деление и умножение:
0 , 5 – 2 · – 7 + 2 3 ÷ 2 3 4 · 11 12 = 1 2 – ( – 14 ) + 2 3 ÷ 11 4 · 11 12
1 2 – ( – 14 ) + 2 3 ÷ 11 4 · 11 12 = 1 2 – ( – 14 ) + 2 3 · 4 11 · 11 12 = 1 2 – ( – 14 ) + 2 9 .
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
1 2 – ( – 14 ) + 2 9 = 1 2 + 14 + 2 9 = 14 + 13 18 = 14 13 18 .
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0 , 5 · ( 0 , 76 – 0 , 06 ) .
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом – умножение.
0 , 5 · ( 0 , 76 – 0 , 06 ) = 0 , 5 · 0 , 7 = 0 , 35 .
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1 + 2 · 1 + 2 · 1 + 2 · 1 – 1 4 .
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1 + 2 · 1 + 2 · 1 + 2 · 1 – 1 4 = 1 + 2 · 1 + 2 · 1 + 2 · 3 4
1 + 2 · 1 + 2 · 1 + 2 · 3 4 = 1 + 2 · 1 + 2 · 2 , 5 = 1 + 2 · 6 = 13 .
В нахождении значений выражений со скобками главное – соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями – 2 · 3 – 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 .
Сначала вычисляем подкоренные выражения.
– 2 · 3 – 1 + 60 ÷ 4 3 = – 6 – 1 + 15 3 = 8 3 = 2
2 , 2 + 0 , 1 · 0 , 5 = 2 , 2 + 0 , 05 = 2 , 25 = 1 , 5 .
Теперь можно вычислить значение всего выражения.
– 2 · 3 – 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 = 2 + 3 · 1 , 5 = 6 , 5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3 + 1 3 – 1 – 1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3 + 1 3 – 1 = 3 – 1 .
3 + 1 3 – 1 – 1 = 3 – 1 – 1 = 1 .
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 2 3 · 4 – 10 + 16 1 – 1 2 3 , 5 – 2 · 1 4 .
Начинаем вычислять по порядку.
2 3 · 4 – 10 = 2 12 – 10 = 2 2 = 4
16 · 1 – 1 2 3 , 5 – 2 · 1 4 = 16 * 0 , 5 3 = 16 · 1 8 = 2 .
Осталось только провести операцию сложение и узнать значение выражения:
2 3 · 4 – 10 + 16 1 – 1 2 3 , 5 – 2 · 1 4 = 4 + 2 = 6 .
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2 – 2 5 · 4 5 – 1 + 3 1 3 6 .
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2 – 2 5 · 4 5 – 1 + 3 1 3 6 = 2 – 2 5 · 2 2 5 – 1 + 3 1 3 · 6
2 – 2 5 · 2 2 5 – 1 + 3 1 3 · 6 = 2 – 2 5 · 2 2 · 5 – 2 + 3 2 = 2 2 · 5 – 2 – 2 5 + 3 2
2 2 · 5 – 2 – 2 5 + 3 2 = 2 – 2 + 3 = 1 4 + 3 = 3 1 4
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3 , 2 2 – 3 · 7 – 2 · 3 6 ÷ 1 + 2 + 3 9 – 6 ÷ 2 .
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3 , 2 2 = 3 , 2 ÷ 2 = 1 , 6
7 – 2 · 3 6 = 7 – 6 6 = 1 6
1 + 2 + 3 9 – 6 ÷ 2 = 1 + 2 + 3 9 – 3 = 6 6 = 1 .
Перепишем наше выражение и вычислим его значение:
1 , 6 – 3 · 1 6 ÷ 1 = 1 , 6 – 0 , 5 ÷ 1 = 1 , 1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 2 5 – 1 – 2 5 – 7 4 – 3 .
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
2 5 – 1 = 2 5 + 1 5 – 1 5 + 1 = 2 5 + 1 5 – 1 = 2 5 + 2 4
Исходное выражение принимает вид:
2 5 – 1 – 2 5 – 7 4 – 3 = 2 5 + 2 4 – 2 5 – 7 4 – 3 .
Вычислим значение этого выражения:
2 5 + 2 4 – 2 5 – 7 4 – 3 = 2 5 + 2 – 2 5 + 7 4 – 3 = 9 4 – 3 = – 3 4 .
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log 2 4 + 2 · 4 можно сразу вместо log 2 4 записать значение этого логарифма, а потом выполнить все действия. Получим: log 2 4 + 2 · 4 = 2 + 2 · 4 = 2 + 8 = 10 .
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log 5 – 6 ÷ 3 5 2 + 2 + 7 . Имеем:
log 5 – 6 ÷ 3 5 2 + 2 + 7 = log 3 27 + 7 = 3 + 7 = 10 .
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 .
log 2 log 2 256 = log 2 8 = 3 .
По свойству логарифмов:
log 6 2 + log 6 3 = log 6 ( 2 · 3 ) = log 6 6 = 1 .
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log 5 729 log 0 , 2 27 = log 5 729 log 1 5 27 = log 5 729 – log 5 27 = – log 27 729 = – log 27 27 2 = – 2 .
Теперь можно переходить к вычислению значения исходного выражения.
log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 = 3 + 1 + – 2 = 2 .
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: t g 2 4 π 3 – sin – 5 π 2 + cosπ .
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
Подставляем значения в выражение и вычисляем его значение:
t g 2 4 π 3 – sin – 5 π 2 + cosπ = 3 2 – ( – 1 ) + ( – 1 ) = 3 + 1 – 1 = 3 .
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos 2 π 8 – sin 2 π 8 cos 5 π 36 cos π 9 – sin 5 π 36 sin π 9 – 1 .
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos 2 π 8 – sin 2 π 8 cos 5 π 36 cos π 9 – sin 5 π 36 sin π 9 – 1 = cos 2 π 8 cos 5 π 36 + π 9 – 1 = cos π 4 cos π 4 – 1 = 1 – 1 = 0 .
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
Корни, степени, логарифмы и т.д. заменяются их значениями.
Выполняются действия в скобках.
Оставшиеся действия выполняются по порядку слева направо. Сначала – умножение и деление, затем – сложение и вычитание.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения – 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 .
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 . Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π
Теперь можно узнать значение синуса:
sin π 6 + 2 · 2 π 5 + 3 π 5 = sin π 6 + 2 π = sin π 6 = 1 2 .
Вычисляем значение подкоренного выражения:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 4 = 2 .
Со знаменателем дроби все проще:
Теперь мы можем записать значение всей дроби:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 = 2 2 = 1 .
С учетом этого, запишем все выражение:
– 1 + 1 + 3 9 = – 1 + 1 + 3 3 = – 1 + 1 + 27 = 27 .
– 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 = 27 .
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 – sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56 + 8 – 3 , 789 ln e 2 – 56 + 8 – 3 , 789 ln e 2 также равно нулю.
Еще один прием, позволяющий ускорить процесс – использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями – сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 2 3 – 1 5 + 3 · 289 · 3 4 3 · 2 3 – 1 5 + 3 · 289 · 3 4 . Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 1 3 .
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0 , 5 x – y при заданных x = 2 , 4 и y = 5 .
Подставляем значения переменных в выражение и вычисляем:
0 , 5 x – y = 0 , 5 · 2 , 4 – 5 = 1 , 2 – 5 = – 3 , 8 .
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х + 3 – х , очевидно, имеет значение 3 , и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения x x равно единице для всех положительных иксов.
Конспект урока по алгебре в 7 классе. Тема:” Числовые выражения”.
план-конспект урока по алгебре (7 класс) на тему
Тема: ” Числовые выражения”.
Скачать:
Вложение Размер
urok_2.docx 15.99 КБ
Предварительный просмотр:
Конспект урока по алгебре в 7 классе.
Тема: « Числовые выражения».
Учебник « Алгебра 7 класс», авторы Ю. М. Колягин и др.
Учитель: Михеева Татьяна Юрьевна
Санкт- Петербург, ГБОУ Лицей 389 «ЦЭО»
– ввести понятие «числового выражения»;
– ввести понятие «значение числового выражения»;
– сформировать умение находить значение числового выражения, выполняя действия над числами и используя скобки.
– актуализация опорных знаний;
– объяснение нового материала;
– подведение итогов урока.
– Здравствуйте, ребята. Сегодня на уроке мы с вами введем понятие « числового выражения», опираясь на приобретенные ранее знания. Посмотрите, пожалуйста, на доску и устно вычислите следующие выражения:
Объяснение нового материала:
При решении этих и многих других задач приходится над заданными числами производить арифметические действия: сложение, вычитание, умножение и деление.
Определение: Числовое выражение – выражение, состоящее из чисел и знаков действий.
Но часто, прежде чем доводить до конца каждое из этих действий, удобно заранее указать порядок (план), следуя которому надо производить эти действия. Этот план сводится к тому, что по данным задачи с помощью чисел, знаков действий и скобок составляется числовое выражение.
Приведем примеры числовых выражений:
5 ; (7+3,5)×2 ; -40+31×3÷2; 25÷5-3×8+96.
Если в числовом выражении выполнить все указанные в нем действия, то в результате получим действительное число, про которое говорят, что оно равно данному числовому выражению и называется значением выражения.
Запишем определение: Найти значение числового выражения – это значит выполнить все действия в нем.
Пример: найти значение числового выражения.
Когда мы с вами начинаем вычисления, мы, конечно, предполагаем, что все действия возможно осуществить. Поясним эти слова.
Всегда возможно произвести сложение, вычитание и умножение любых чисел. А вот с делением иногда возникают вопросы. Мы можем делить одно число на другое, только если делитель не равен нулю! На нуль делить нельзя.
Если в выражении на некотором этапе вычисления требуется делить на нуль, то это требование неосуществимо. Такое выражение не имеет смысла.
Определите: имеют ли смысл выражения (устно)
(3,5+0,8)/(6,2-8+1,8)= (не имеет смысла )
2/3-2= (имеет смысл )
0,48×0= (имеет смысл )
Теперь рассмотрим несколько задач.
Вспомним, как найти дробь от числа?
Чтобы найти дробь от числа, надо это число умножить на дробь.
Найти 2/3 от числа 60.
Как найти число по его дроби?
Чтобы найти число по известной величине его дроби, надо поделить эту величину на данную дробь.
Найти число, если известно, что 1/3 от него равна 9.
Что такое процент?
Одна сотая часть любой величины или числа называются процентом.
Как найти процент от данного числа?
Чтобы найти процент от данного числа, надо записать процент в виде дроби и умножить это число на дробь.
Найти 8% от числа 400.
Как найти число по его проценту?
Чтобы найти число по его проценту, надо записать процент в виде дроби и разделить эту величину на дробь.
Найти число, если 16% этого числа равны 80.
Формирование умений и навыков:
Решаем № 1 (стр.10) – у доски
№ 5 (стр.10) – у доски
№ 8 (стр.11) – у доски
Подведем итоги урока:
– Что называется числовым выражением?
– Что называется значением числового выражения?
– Когда числовое выражение имеет смысл, а когда – нет? (примеры )
– Каков порядок выполнения действий при нахождении значения числового выражения?
Ребята, наш урок подошел к концу. Запишите, пожалуйста, домашнее задание:
Выучить теорию п.1
№ 7 (2,4), №8 (2,4,6).
По теме: методические разработки, презентации и конспекты
План – конспект урока по алгебре, 9 класс “Соотношения между тригонометрическими функциями одного и того же угла”
Основное назначение урока заключается в систематизации знаний учащихся по изучаемой теме, создания условий для осознанного повторения ранее изученного материала, возможностей для максимального развити.
Конспект урока по алгебре 8 класс “Решение квадратных уравнений графическим способом”
Конспект урока-практикума по алгебре с тестовыми заданиями.
План-конспект урока по алгебре (7 класс) .Урок по теме: “Разложение многочлена на множители с помощью формул сокращённого умножения.”
Урок обобщения и закрепления по теме:”Разложение многочлена на множители с помощью формул сокращённого умножения.” На уроке отрабатываются навыки применения формул при решении уравнений , а так .
Конспект урока по алгебре 7 класса На тему: Произведение разности двух выражений на их сумму.
Тема урока значимая в курсе математики т.к. формулы сокращенного умножения применяются на протяжении всего периода обучения математике, они используются при умножении многочленов, упрощении алгебраиче.
Открытый урок математики в 5 классе Тема: «Числовые и буквенные выражения»
урок математики в 5 классе Тема: “Числовые и буквенные выражения” Урок по адаптации учащихся 5 класса.
Алгебре 8 класс. Тема “Числовые неравенства и их свойства”. Тест.
Тест по теме с выбором ответов.
Конспект урока математики в 6 классе по теме “Выражения, содержащие сложение и вычитание”
Пробудив интерес ученика к процессу изучения материала, легче усваиваются понятия и быстрее формируются достаточно прочные знания.Выход нашелся сам собой. Что с детства читают мамы своим детям, что ба.
Числовые и буквенные выражения
О чем эта статья:
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
23 + 5 = 28
5 – 2 = 3
52 * 3 = 156
28 : 7 = 4
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
(5 * 3) – (5 * 2) = 5
6 : (7 – 4) = 2
(45 + 45) : 9 = 10
11 * (5 * 5) = 275
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
– — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Сначала выполняется действие, записанное в скобках.
Затем выполняется деление/умножение.
В последнюю очередь выполняется сложение/вычитание.
Пример 1. Найдите значение числового выражения: 3 * (2 + 8) – 4
2 + 8 = 10
3 * 10 = 30
30 – 4 = 26
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
6 + 7 = 13
13 + 2 = 15
13 * 15 = 195
(6 + 7) * (13 + 2) = 195
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
Сначала находим значение первого выражения:
6 + 8 = 14

Затем находим значение второго выражения:
2 * 2 = 4

Сравниваем получившиеся результаты:
14 больше 4
14 > 4
6 + 8 > 2 * 2
Пример 2. Сравните следующие числовые выражения:
5 * (12 – 2) – 7 и (115 + 9) – (7 – 3)
Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:
12 – 2 = 10
5 * 10 = 50
50 – 7 = 43
5 * (12 – 2) – 7 = 43

Затем находим значение:
115 + 9 = 124
7 – 3 = 4
124 – 4 = 120

Сравниваем полученные результаты:
43 меньше 120
43
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Например:
(5 + a) * 7
7 * (x – 2)
(6 – 2) + (3 + x)
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Сначала следует прочитать его полностью.
Затем оно записывается.
Третьим шагом идет подстановка значения неизвестного в выражение.
А затем производится вычисление, согласно очередности выполнения арифметических действий.
Пример 1. Найдите значение выражения: 5 + x.
Читаем: найдите сумму числа 5 и x.
Подставляем вместо неизвестного x число 4.
Вычисляем: 5 + 4 = 9.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
Подставляем вместо неизвестного a число 2.
Вычисляем 4 + 2 = 6.
Подставляем вместо неизвестного x число 5.
Вычисляем 2 + 5 = 10.
Находим произведение 6 * 10 = 60.
Записываем результат: (4 + 2) * (2 + 5) = 60.
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Например, в выражении x + a – 8
x — переменная
a — переменная
Если вместо переменных подставить числа, то буквенное выражение x + a – 8 станет числовым выражением. Вот так:
подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 – 8.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
После подстановки значения переменных находим значение x + a – 8 = 5 + 10 – 8 = 7.
Часто можно встретить буквенные выражения, записанные следующим образом:
5x – 4a
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x – 4a = 5*x – 4*a
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Сумма 6 и a.
Разность 8 и x.
Сумма x – 2 и 6
Разность 15 и x – y
Сумма 45 + 5 и 12 – 6
6 + a.
8 – x
(x – 2) + 6
15 – (x – y)
(45 + 5) + (12 – 6).
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: (b – 345) + (180 + x).
Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 – y) – (a – b).
Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Задание шесть.
Вычислите:
(500 + 300) : a – 15,
при условии, что a = 10.
Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 – 15
Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 – 15 = 65.
Ответ: (500 + 300) : 10 – 15 = 65.
Задание семь.
Вычислите:
(270 – 120) * (x – 10),
при условии, что x = 45.
Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 – 120) * (45 – 10).
Затем выполняем сначала арифметическое действие в скобках: 270 – 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 – 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250
Ответ: (270 – 120) * (45 – 10) = 5 250.
Задание восемь.
Вычислите:
(50 * x) – (3 * y)
при условии, что x = 2; y = 10
Подставляем число 2 вместо переменной x
(50 * 2) – (3 * y).
Подставляем число 10 вместо переменной y
(50 * 2) – (3 * 10).
Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 – 30 = 70
§ 1. Числовые и алгебраические выражения (продолжение)
3) Разделим с на 4:
4) В = 25 • 37 • 0,4. Опять-таки можно проводить вычисления «в лоб», т. е. вычислить 25*37, затем то, что получится, умножить на 0,4. Но думающий человек (а таким всегда является культурный человек) воспользуется переместительным и сочетательным законами умножения и будет вычислять так:
25 • 37 0,4 = (25 • 0,4) • 37 = 10 • 37 = 370.
5) Осталось разделить числитель а на знаменатель b. Получим (разделили числитель и знаменатель дроби на 5, т. е. сократили дробь).
О т в е т:
А теперь вместе проанализируем, какие сведения из математики нам пришлось вспомнить в процессе решения примера (причём не просто вспомнить, но и использовать).
1. Порядок арифметических действий.
2. Переместительный закон сложения: а + b = b + а.
3. Переместительный закон умножения: аb = bа.
4. Сочетательный закон сложения:
а + b + с = (а + b) + с = а + (b + с).
5. Сочетательный закон умножения: аbс = (ab)c = а(bс).
6. Понятия обыкновенной дроби, десятичной дроби, отрицательного числа.
7. Арифметические операции с десятичными дробями.
8. Арифметические операции с обыкновенными дробями.
9. Основное свойство обыкновенной дроби: (значение дроби не изменится, если её числитель и знаменатель одновременно умножить на одно и то же число или разделить на одно и то же число, отличное от нуля). Это свойство позволило нам преобразовать дробь к виду (числитель и знаменатель дроби одновременно умножили на одно и то же число 3). Оно же позволило нам сократить дробь (числитель и знаменатель дроби одновременно разделили на одно и то же число 5).
10. Правила действий с положительными и отрицательными числами.
Всё это вы знаете, но ведь всё это — алгебраические факты. Таким образом, некоторое знакомство с алгеброй у вас уже состоялось в младших классах. Основная трудность, как видно уже из примера 1, заключается в том, что таких фактов довольно много, причём их надо не только знать, но и уметь использовать, как говорят, «в нужное время и в нужном месте». Вот этому и будем учиться.

И последнее, чтобы закончить обсуждение примера 1. То число, которое получается в результате упрощений числового выражения (в данном примере это было число называют значением числового выражения.
Если дано алгебраическое выражение, то можно говорить о значении алгебраического выражения, но только при конкретных значениях входящих в него букв. Например, алгебраическое выражение а + b при а = 5, b = 7 имеет значение 12 (поскольку а + b = 5 + 7 = 12); при а = -16, b = -14 оно имеет значение -30 (так как а + b = -16 + (-14) = -16 – 14 = -30). Алгебраическое выражение а 2 – 3b (что такое а 2 , помните? — это а • а) при а = -2, b = 0,4 принимает вид числового выражения (-2) 2 – 3 • 0,4; упрощая, получаем 4 – 1,2 = 2,8 — это и есть значение алгебраического выражения а 2 – 3b при а = -2, b = 0,4.
Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т.е. можно менять значения букв), эти буквы называют переменными.