Шестнадцатеричный код – алгоритмы перевода и примеры преобразований чисел
Правила перевода целых чисел
Результатом является целое число.
1. Из десятичной системы счисления – в двоичную и шестнадцатеричную:
- исходное целое число делится на основание системы счисления, в которую переводится (2 или 16); получается частное и остаток;
- если полученное частное не делится на основание системы счисления так, чтобы образовалась целая часть, отличная от нуля, процесс умножения прекращается, переходят к шагу в). Иначе над частным выполняют действия, описанные в шаге а);
- все полученные остатки и последнее частное преобразуются в соответствии с таблицей в цифры той системы счисления, в которую выполняется перевод;
- формируется результирующее число: его старший разряд – полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа – первый остаток от деления, а старший – последнее частное.
Пример 3.1. Выполнить перевод числа 19 в двоичную систему счисления: 
Пример 3.2. Выполнить перевод числа 19 в шестнадцатеричную систему счисления: 
Пример 3.3. Выполнить перевод числа 123 в шестнадцатеричную систему счисления: 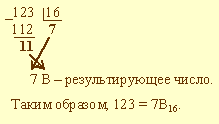
2. Из двоичной и шестнадцатеричной систем счисления – в десятичную. В этом случае рассчитывается полное значение числа по формуле.
Пример 3.4. Выполнить перевод числа 1316 в десятичную систему счисления. Имеем:
1316 = 1*16 1 + 3*16 0 = 16 + 3 = 19.
Таким образом, 1316 = 19.
Пример 3.5. Выполнить перевод числа 100112 в десятичную систему счисления. Имеем:
100112 = 1*2 4 + 0*2 3 + 0*2 2 + 1*2 1 + 1*2 0 = 16+0+0+2+1 = 19.
Таким образом, 100112 = 19.
3. Из двоичной системы счисления в шестнадцатеричную:
- исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4;
- каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицей
Пример 3.6. Выполнить перевод числа 100112 в шестнадцатеричную систему счисления.
Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем:

4. Из шестнадцатеричной системы счисления в двоичную:
- каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады;
- незначащие нули в результирующем числе отбрасываются.
Пример 3.7. Выполнить перевод числа 1316 в двоичную систему счисления.
По таблице имеем: 116 = 12 и после дополнения незначащими нулями 12 = 00012; 316 = 112 и после дополнения незначащими нулями 112 = 00112. Тогда 1316 = 000100112. После удаления незначащих нулей имеем 1316 = 100112.
- исходная дробь умножается на основание системы счисления, в которую переводится (2 или 16);
- в полученном произведении целая часть преобразуется в соответствии с таблицей в цифру нужной системы счисления и отбрасывается – она является старшей цифрой получаемой дроби;
- оставшаяся дробная часть вновь умножается на нужное основание системы счисления с последующей обработкой полученного произведения в соответствии с шагами а) и б).
- процедура умножения продолжается до тех пор, пока ни будет получен нулевой результат в дробной части произведения или ни будет достигнуто требуемое количество цифр в результате;
- формируется результат: последовательно отброшенные в шаге б) цифры составляют дробную часть результата, причем в порядке уменьшения старшинства.
Пример 3.8. Выполнить перевод числа 0,847 в двоичную систему счисления. Перевод выполнить до четырех значащих цифр после запятой.
Имеем:
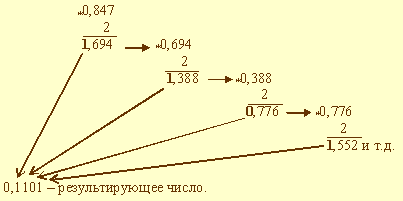
В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата. Очевидно, это привело к потере ряда цифр.
Таким образом, 0,847 = 0,11012.
Пример 3.9. Выполнить перевод числа 0,847 в шестнадцатеричную систему счисления. Перевод выполнить до трех значащих цифр.
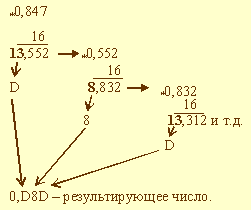
В данном примере также процедура перевода прервана. Таким образом, 0,847 = 0,D8D2.
2. Из двоичной и шестнадцатеричной систем счисления – в десятичную. В этом случае рассчитывается полное значение числа по формуле, причем коэффициенты ai принимают десятичное значение в соответствии с таблицей.
Пример 3.10. Выполнить перевод из двоичной системы счисления в десятичную числа 0,11012. Имеем:
0,11012 = 1*2 -1 + 1*2 -2 + 0*2 -3 +1*2 -4 = 0,5 + 0,25 + 0 + 0,0625 = 0,8125.
Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в двоичную дробь была прервана.
Таким образом, 0,11012 = 0,8125.
Пример 3.11. Выполнить перевод из шестнадцатеричной системы счисления в десятичную числа 0,D8D16. Имеем:
0,D8D16 = 13*16 -1 + 8*16 -2 + 13*16 -3 = 13*0,0625 + 8*0,003906 + 13* 0,000244 = 0,84692.
Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в шестнадцатеричную дробь была прервана.
Таким образом, 0,D8D16 = 0,84692.
3. Из двоичной системы счисления в шестнадцатеричную:
- исходная дробь делится на тетрады, начиная с позиции десятичной точки вправо. Если количество цифр дробной части исходного двоичного числа не кратно 4, оно дополняется справа незначащими нулями до достижения кратности 4;
- каждая тетрада заменяется шестнадцатеричной цифрой в соответствии с таблицей.
Пример 3.12. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,11012. Имеем:
0,11012 = 0,11012 В соответствии с таблицей 11012 = D16. Тогда имеем 0,11012 = 0,D16.
Пример 3.13. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,00101012.
Поскольку количество цифр дробной части не кратно 4, добавим справа незначащий ноль: 0,00101012 = 0,001010102. В соответствии с таблицей 00102 = 102 = 216 и 10102 = A16. Тогда имеем 0,00101012 = 0,2A16.
4. Из шестнадцатеричной системы счисления в двоичную:
- каждая цифра исходной дроби заменяется тетрадой двоичных цифр в соответствии с таблицей;
- незначащие нули отбрасываются.
Пример 3.14. Выполнить перевод из шестнадцатеричной системы счисления в двоичную числа 0,2А16.
По таблице имеем 216 = 00102 и А16 = 10102. Тогда 0,2А16 = 0,001010102.
Отбросим в результате незначащий ноль и получим окончательный результат: 0,2А16 = 0,00101012.
Правило перевода дробных чисел
Отдельно переводится целая часть числа, отдельно – дробная. Результаты складываются.
Пример 3.15. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847. Перевод выполнять до трех значащих цифр после запятой.
Представим исходное число как сумму целого числа и правильной дроби:
19,847 = 19 + 0,847.
Как следует из примера 3.2, 19 = 1316; а в соответствии с примером 3.9 0,847 = 0,D8D16. Тогда имеем:
19 + 0,847 = 1316 + 0,D8D16 = 13,D8D16.
Таким образом, 19,847 = 13,D8D16.
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode
Шестнадцатеричная система счисления
Системы счисления – одна из самых главных основ информатики. Практически ни в одной школе и ни в одном университете не пропускают данную тему, но зачастую именно с переводом шестнадцатеричной системы у многих возникают проблемы, хотя это не такая уж сложная задача, и её перевод практически не отличается от других систем счисления.
Давайте рассмотрим эту систему поподробнее.
Для чего нужна шестнадцатеричная система
Итак, шестнадцатеричная система счисления, как следует из названия, имеет в своём основании число 16. Почему так? Дело в том, что единица информации в информатике – это бит. Восемь бит образуют байт. Также информационной среде существует такое понятие, как машинное слово – это минимальная единица данных, представляющая собой шестнадцать бит, то есть два байта. Считается, что машинное слово – это минимальная величина разрядности регистров процессора, при которой можно работать с ЭВМ.
Так вот, как мы знаем, компьютер работает на двоичном коде. Однако, если Вы когда-нибудь переводили числа из двоичной системы в десятичную, то замечали, что в ней бывает довольно много разрядов, особенно при переводе больших чисел, например, перевод числа 5132 в двоичной системе будет записано так:

Как можно увидеть, при переводе в двоичную систему этого числа у нас получилось аж 13 разрядов (с 0 до 12). Довольно муторно, а главное, занимает много места на письме и отнимает много времени для перевода.
Именно для этого придумали восьмеричную и шестнадцатеричную системы счисления, для этого придумали и байты. Эти системы помогают сократить затраты на перевод чисел и привести их к более приятному визуальному виду.
Если перевести то же число 5132 в восьмеричную систему счисления, то получится «более сокращённая версия» двоичного кода:

Как мы видим, количество символов сократилось, так как разрядность уменьшилась до 5 (с 0 до 4).
Как можно уже понять, шестнадцатеричная система ещё сильнее сокращает разрядность (с 0 до 3) и ещё сильнее сжимает на письме переведённое число:

Человеку такой вид записи в любом случае удобнее, чем бесконечные нули и единицы.
Таким образом, шестнадцатеричная система используется довольно широко в современных информационных системах. Например, при помощи неё указываются коды цветовых схем, данная система используется для записи кодов ошибок, а также для программирования на языках низкого уровня типа Ассемблера, шестнадцатеричную систему зачастую используют для предоставления данных и адресов в малоразрядных ЭВМ.
Как перевести из десятичной системы в шестнадцатеричную
Выше мы уже немного затронули процесс перевода чисел. Теперь мы рассмотрим его подробнее и на примерах.
Но прежде чем начать, надо узнать одну очень важную особенность шестнадцатеричной системы.
Так как система имеет своим основанием число 16, то, следовательно, всего в этой системе имеется 16 цифр, но если первые десять цифр (0-9) вполне привычные для нас, то остальные имеют вид не совсем цифровой, но, тем не менее, являются цифрами, а именно значения A, B, C, D, E, F, которые соответствуют нашим привычным числам с 10 до 15. Все цифры шестнадцатеричной системы и их «аналоги» в десятичной записаны в таблице ниже.

Итак, допустим, у нас есть число 40 563 в десятичной системе счисления. Переведём его в шестнадцатеричную.
- Сначала мы просто делим наше исходное число 40 563 на 16 в столбик. В частном у нас получилось 2 535, если умножить это число на 16, то получится 40 560, а в остатке 3. Эту тройку мы выделяем.

- Теперь мы делим 2 535, и тоже на 16, и тоже абсолютно таким же образом. Частное – 158, 16*158 = 2 528, а в остатке 7. Остаток так же, как и в тот раз, выделяем.

- Делим полученные частные до тех пор, пока они не станут меньше 16 , тогда деление заканчивается. Делим 158 на 16, и находим остаток от этого деления.

Остаток от деления – 14, а частное, полученное при делении 158 на 16 равно 9. Так как 9 меньше 16, то процесс вычислений закончен, а 9 также выделяется.
- Процесс преобразования десятичного числа в шестнадцатеричное почти окончен. Для того, чтобы получить его, надо всего лишь выписать выделенные числа справа налево (т.е. в данном случае от девятки к тройке), НО, как мы писали выше, у шестнадцатеричной системы свой особый «алфавит» с 10 по 15. И как раз один из наших «остатков» (число 14) вписывается в этот диапазон, поэтому надо посмотреть в таблице, либо просто самостоятельно посчитать, что в шестнадцатеричной системе 14 будет буквой Е.
Итого весь процесс преобразования приведён на следующем изображении:

Таким образом мы научились переводить числа из десятичной системы в шестнадцатеричную. Теперь давайте попробуем сделать обратное преобразование, но уже с другим числом.
Как перевести из шестнадцатеричной системы в десятичную
Перевести шестнадцатеричное число в привычное нам десятичное также совсем не сложно, более того, мы уже делали это в самом начале статьи, когда сравнивали двоичную, восьмеричную и шестнадцатеричную системы счислений, теперь же разберём этот процесс более подробно.
Давайте сразу приступим к примеру и переведём шестнадцатеричное число 1C3B3 в десятичную систему.
По сути, процесс перевода можно разделить на 2 этапа:
- Мы справа налево отделяем от числа все цифры и умножаем каждую из них на 16, и всё это складываем:

Также обязательно необходимо перевести буквенные обозначения шестнадцатеричной системы в числовые, чтобы можно было посчитать их в десятичном виде, то есть, для данного случая, перевести B в 11 и C в 12.
- После того, как мы сделали этот шаг, нам необходимо пронумеровать разряды чисел. Делается это просто – мы приписываем ко всем числам 16, на которые мы умножали наши исходные цифры, степени, начиная с нулевой:

Теперь нам остаётся только перемножить и сложить всё это:

Таким образом, мы превратили шестнадцатеричное число 1C3B3 в десятичное число 115 635.
Как видите, ничего сложного. Также у нас на сайте имеется статья, описывающая процесс перевода чисел из шестнадцатеричной системы в двоичную.
Спасибо за прочтение!
Шестнадцатеричный код — алгоритмы перевода и примеры преобразований чисел
Для перевода команд пользователя на машинный язык применяются специальные системы представления данных. С их помощью осуществляется работа с регистрами оперативной памяти, внешними и внутренними накопителями, а также другими логическими устройствами. В первом и во втором случаях применяется шестнадцатеричный код. Его конвертация осуществляется по определенным алгоритмам. Для их использования следует немного разобраться в теоретических аспектах.

Общие сведения
Система счисления — метод символьного типа для записи чисел с помощью определенных знаков. Последние записываются посредством чисел и цифр. Однако не все понимают логического смысла последних терминов. Числом называется некоторая абстрактное значение, характеризующее количественные характеристики какой-либо величины, явления или процесса. Цифра является знаком, который необходим для записи числа.
Цифры бывают 2 видов: арабскими и римскими. Первые являются самыми распространенными. Они представлены знаковым интервалом от 0 до 9. Чисел больше, и поэтому используется набор цифр. Для этого и были придуманы системы исчисления. Они делятся на четыре группы:

К первой группе относятся все разрядные системы, в которых положение и порядок знака играет важную роль. От этого зависит значение величины. Если изменить положение цифр, то число изменится.
Во втором случае простым примером является массив данных с параметром «ключ — значение». Например, массив ассоциативного типа состоит из 3 элементов: ‘login’ -> ‘Ivan10’, ‘pass’ -> ‘12345’ и ‘name’ -> ‘Иван’. В этом случае данные можно менять местами, поскольку логика сохранится.
Смешанной является система, в которой присутствуют данные позиционной и непозиционной групп.Простой пример — деньги. Существуют два типа денежных знаков: монеты и купюры. Например, техника стоит 5250 рублей 50 копеек.
Для получения данной суммы следует использовать некоторое количество купюр и монет: 5250,50 = (5000 + 200 + 50) рублей + 50 копеек.
Унарной называется единичная система с одной цифрой. Последняя может быть представлена в виде 1, черты, креста и любого целого значения. Иными словами, каждый знак соответствует 1. Например, запись «1111111» эквивалентна «|||||||». Если расшифровать ее, то получится число 7. В книге Даниэля Дефо «Робинзон Крузо» герой применял данную систему для подсчета дней, проведенных на острове. Детей обучают математике на начальном уровне с помощью счетных палочек. Если вспомнить историю, то древние люди тоже пользовались унарным счислением.
Позиционные системы в программировании
Наиболее востребованными в IT-сфере являются двоичный и шестнадцатеричный коды. Они применяются для перевода десятичной системы счисления, которая понятна человеку, в машинный язык. Двоичная состоит из двух переменных, которые принимают единичное (1) или нулевое (0) значения. Это очень просто реализовать в электронике и микросхемотехнике.

Микропроцессор персонального компьютера является микросхемой. Она состоит из множества транзисторов, способных кодировать 0 и 1. Схему соединения полупроводниковых приборов составляют так, чтобы они имели два состояния (открыт и закрыт). Кроме того, реализация двоичной системы может быть выполнена в любом устройстве, которое потребляет электрический ток. Наличие кодируется как 1, а отсутствие — 0.
Берутся также некоторые физические процессы: наличие света, сопротивления, намагниченности и так далее. С системой можно связать разные величины, которые имеют два состояния. Новичкам рекомендуется сначала полностью освоить перевод из десятичной системы счисления в двоичную и обратно. После этого следует приступить к изучению шестнадцатеричного кода, расшифровка которого существенно отличается.
Работа с двоичным кодом
Выполнять манипуляции с двоичным кодом достаточно просто. Для этого следует знать основные правила и методы конвертации десятичной системы в двоичную.
Для преобразования IT-специалисты предлагают 3 метода:
- деление с отсечением остатка;
- представление в виде степеней двойки;
- автоматизированный.
Первый и второй способы используются на первоначальных этапах знакомства с системами. Они считаются ресурсоемкими, поскольку отнимают время. Последний реализуется с помощью специальных программ, поддерживающих конвертацию из одной системы в другую. Этим методом пользуются все программисты. В различных операционных системах есть приложения, работающие в таком режиме (например, калькулятор Windows).
Однако нужно подробнее разобрать первые два метода, поскольку задачи на конвертацию могут быть на экзаменах или контрольных.
Деление с отсечением остатка
Начинающему программисту необходимо обязательно знать алгоритм преобразования, и уметь применять его на практике. К

роме того, на экзаменах по дисциплинам с IT-уклоном может быть задача, в которой следует выполнить конвертацию из одной системы счисления в другую.
Перевод числа из десятичной в двоичную осуществляется по такому алгоритму:
Для наглядного примера стоит применить алгоритм на практике.
Для перевода числа 13 нужно выполнить следующие шаги:

Нужно обратить внимание на форму записи в 6 пункте.
Таким способом правильно записывается число в системах счисления.
Можно применять также вместо <2>нижний индекс, указывающий искомую систему.
Последний пункт нужно выполнять постоянно, поскольку это поможет избежать проблем при расчетах.
Если ничего нет под рукой, то можно произвести возведение в степень. Это делается следующим образом: [1011] <2>= 2 3 + 0 + 2 1 + 2 0 = 8 + 0 + 2 + 1 = [13]<10>.
Степенной метод
Для реализации этого метода необходимо воспользоваться таблицей степеней двойки (табл. 1). Ее можно составить самостоятельно или скачать из интернета. Суть метода сводится также к вычислениям и подборам значений.
| Показатель степени, n | Результат возведения |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
Таблица 1. Степень двойки до 6 и ее значения.
Специалисты рекомендуют воспользоваться обыкновенным калькулятором, который разрешен на экзаменах или тестах. Кроме того, следует составить таблицу, поскольку это оптимизирует процесс вычислений. Для конвертации есть специальный алгоритм:

Для проверки рекомендуется воспользоваться специальным калькулятором или выполнить сложение всех значений степеней. Для примера можно рассмотреть конвертацию числа 118 в двоичный код. Операция выполняется таким образом:
Чтобы проверить в ручном режиме, нужно произвести обратные вычисления: 2 6 + 2 5 + 2 4 + 0 + 2 2 + 2 1 + 0 = [118]<10>.
Шестнадцатеричный формат
Осуществить конвертацию из десятичного в шестнадцатеричный код (HEX — hexadecimal) можно только с использованием программ. Ручной метод основан на двойной конвертации. Для его реализации нужно перевести число, записанное в десятичной системе, в двоичный код, а затем в шестнадцатеричный.

Основанием является целочисленное значение, равное 16. Система состоит из арабских цифр от 0 до 9, а также букв, обозначающих конкретные значения: А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15. В автоматизированном режиме можно воспользоваться переводчиком шестнадцатеричного кода.
Необходимо отметить, что HEX применяется также в низкоуровневом программировании. Выбор этой системы счисления основан на решении в компьютерной технике применять такую единицу информации, как байт (состоит из 8 битов). Его удобно записывать двумя HEX-цифрами (от 0 до 255, т. е. #00 до #FF). Кроме того, шестнадцатеричный код в текст также конвертируется. Примером этому является кодировка Юникод, в которой для записи символа применяются четыре HEX-цифры. Цвет RGB-формата графического изображения также записывается с его помощью.
Способы записи
Существует несколько форм записи числа, представленного в HEX. Математическая форма выглядит таким образом: [DF5]<16>. Можно также найти запись, в которой вместо <16>стоит нижний индекс. Она применяется в информатике.
Запись отличается в языках программирования, поскольку у каждого из них различный синтаксис и правила написания кода. Основные формы представления HEX следующие:

- В С, С++ и похожих применяется префикс «0х».
- В Ассемблере после числа ставится латинская буква «h».
- В Pascal, Delfi, Basic используется символ «$».
- В HTML и CSS — «#».
- В Python — «0х».
Распространенная ошибка новичков заключается в том, что они неверно указывают HEX-числа. В результате компилятор языка выдает ошибку. Программисты рекомендуют основательно изучить синтаксис языка перед написанием приложений.
Алгоритм конвертации
Перевод в шестнадцатеричный код рекомендуется осуществлять с помощью специальных приложений (конвертеров кода). Если же их нет под рукой, то специалисты рекомендуют использовать специальный алгоритм:

Операции умножения, сложения, вычитания и деления сложны.
Они осуществляются только с помощью специальных программ или онлайн-сервисов.
Не следует путать четверичные с троичными группами, которые используются в восьмеричном коде.
Например, нужно перевести 118 в HEX-код.
Для этого следует воспользоваться описанным алгоритмом:
В некоторых случаях нужно использовать буквы. Например, для перевода числа [11110111] <2>в HEX-код нужно также воспользоваться алгоритмом, разбивая его на тетрады следующим образом: 1111 0111. Первая группа равна 2 3 + 2 2 + 2 1 + 2 0 = [15] <10>= F<16>, а вторая — 0 + 2 2 + 2 1 + 2 0 = 7. Результирующая запись имеет такой вид: [11110111] <2>= [F7]<16>.
Таким образом, HEX-код получил широкое применение в IT-сфере, поскольку он очень удобен для записи массивов информации. Однако для его конвертации в ручном режиме нужно изучить двоичную систему счисления, а также основные алгоритмы преобразования.
Шестнадцатеричный код ☑️ расшифровка системы счисления, как перевести шестнадцатеричное число в десятичное, как переводить из двоичной в шестнадцатеричную систему, примеры преобразований
Для чего нужна шестнадцатеричная система
Итак, шестнадцатеричная система счисления, как следует из названия, имеет в своём основании число 16. Почему так? Дело в том, что единица информации в информатике – это бит. Восемь бит образуют байт. Также информационной среде существует такое понятие, как машинное слово – это минимальная единица данных, представляющая собой шестнадцать бит, то есть два байта. Считается, что машинное слово – это минимальная величина разрядности регистров процессора, при которой можно работать с ЭВМ. Так вот, как мы знаем, компьютер работает на двоичном коде. Однако, если Вы когда-нибудь переводили числа из двоичной системы в десятичную, то замечали, что в ней бывает довольно много разрядов, особенно при переводе больших чисел, например, перевод числа 5132 в двоичной системе будет записано так:

Как можно увидеть, при переводе в двоичную систему этого числа у нас получилось аж 13 разрядов (с 0 до 12). Довольно муторно, а главное, занимает много места на письме и отнимает много времени для перевода. Именно для этого придумали восьмеричную и шестнадцатеричную системы счисления, для этого придумали и байты. Эти системы помогают сократить затраты на перевод чисел и привести их к более приятному визуальному виду. Если перевести то же число 5132 в восьмеричную систему счисления, то получится «более сокращённая версия» двоичного кода:

Как мы видим, количество символов сократилось, так как разрядность уменьшилась до 5 (с 0 до 4). Как можно уже понять, шестнадцатеричная система ещё сильнее сокращает разрядность (с 0 до 3) и ещё сильнее сжимает на письме переведённое число:

Человеку такой вид записи в любом случае удобнее, чем бесконечные нули и единицы.
Таким образом, шестнадцатеричная система используется довольно широко в современных информационных системах. Например, при помощи неё указываются коды цветовых схем, данная система используется для записи кодов ошибок, а также для программирования на языках низкого уровня типа Ассемблера, шестнадцатеричную систему зачастую используют для предоставления данных и адресов в малоразрядных ЭВМ.
Применение шестнадцатеричной системы счисления
Шестнадцатеричная система, как и восьмеричная активно применяется в компьютерных технологиях. При этом, запись чисел гораздо компактнее. В отличии от восьмеричной, которая за годы развития информатики — устарела, шестнадцатеричная — применяется в следующих областях:
- Низкоуровневое программирование (к примеру, ассемблер).
- Стандарт Юникод.
- Шестнадцатеричный цвет (RGB).
- Запись кодов ошибок.
- Представление данных в малоразрядных ЭВМ.
Как перевести из десятичной системы в шестнадцатеричную
Выше мы уже немного затронули процесс перевода чисел. Теперь мы рассмотрим его подробнее и на примерах.
Но прежде чем начать, надо узнать одну очень важную особенность шестнадцатеричной системы.
Так как система имеет своим основанием число 16, то, следовательно, всего в этой системе имеется 16 цифр, но если первые десять цифр (0-9) вполне привычные для нас, то остальные имеют вид не совсем цифровой, но, тем не менее, являются цифрами, а именно значения A, B, C, D, E, F, которые соответствуют нашим привычным числам с 10 до 15. Все цифры шестнадцатеричной системы и их «аналоги» в десятичной записаны в таблице ниже.

Итак, допустим, у нас есть число 40 563 в десятичной системе счисления. Переведём его в шестнадцатеричную.
- Сначала мы просто делим наше исходное число 40 563 на 16 в столбик. В частном у нас получилось 2 535, если умножить это число на 16, то получится 40 560, а в остатке 3. Эту тройку мы выделяем.

- Теперь мы делим 2 535, и тоже на 16, и тоже абсолютно таким же образом. Частное – 158, 16*158 = 2 528, а в остатке 7. Остаток так же, как и в тот раз, выделяем.

- Делим полученные частные до тех пор, пока они не станут меньше 16 , тогда деление заканчивается. Делим 158 на 16, и находим остаток от этого деления.

Остаток от деления – 14, а частное, полученное при делении 158 на 16 равно 9. Так как 9 меньше 16, то процесс вычислений закончен, а 9 также выделяется.
- Процесс преобразования десятичного числа в шестнадцатеричное почти окончен. Для того, чтобы получить его, надо всего лишь выписать выделенные числа справа налево (т.е. в данном случае от девятки к тройке), НО, как мы писали выше, у шестнадцатеричной системы свой особый «алфавит» с 10 по 15. И как раз один из наших «остатков» (число 14) вписывается в этот диапазон, поэтому надо посмотреть в таблице, либо просто самостоятельно посчитать, что в шестнадцатеричной системе 14 будет буквой Е.
Итого весь процесс преобразования приведён на следующем изображении:

Таким образом мы научились переводить числа из десятичной системы в шестнадцатеричную. Теперь давайте попробуем сделать обратное преобразование, но уже с другим числом.
Двоичная система счисления ; основа мироздания.
Вы помните Даосский символ Инь и Янь? Он состоит из двух цветов, из двух понятий: чёрного и белого, мужского и женского, единицы и нуля. Согласно Даосской философии весь мир сформирован именно с помощью двух противоположных
и вместе с тем неразделимых понятий. Просто поражает гениальность древних мудрецов. С помощью единиц и нулей человек создаёт множество цифровых миров. Год от года они становятся всё более реалистичными. Интересно, догадывается
ли герой компьютерной игры, что весь его мир состоит всего из двух цифр или это только мы такие прозорливые :)?
Позиционные системы в программировании
Наиболее востребованными в IT-сфере являются двоичный и шестнадцатеричный коды. Они применяются для перевода десятичной системы счисления, которая понятна человеку, в машинный язык. Двоичная состоит из двух переменных, которые принимают единичное (1) или нулевое (0) значения. Это очень просто реализовать в электронике и микросхемотехнике.
Микропроцессор персонального компьютера является микросхемой. Она состоит из множества транзисторов, способных кодировать 0 и 1. Схему соединения полупроводниковых приборов составляют так, чтобы они имели два состояния (открыт и закрыт). Кроме того, реализация двоичной системы может быть выполнена в любом устройстве, которое потребляет электрический ток. Наличие кодируется как 1, а отсутствие — 0.
Берутся также некоторые физические процессы: наличие света, сопротивления, намагниченности и так далее. С системой можно связать разные величины, которые имеют два состояния. Новичкам рекомендуется сначала полностью освоить перевод из десятичной системы счисления в двоичную и обратно. После этого следует приступить к изучению шестнадцатеричного кода, расшифровка которого существенно отличается.
Шестнадцатеричная система счисления.
В шестнадцатеричной системе счисления одним символом отображаются числа от нуля до шестнадцати. Чтобы не сочинять новых отображений цифр, решили использовать буквы латинского алфавита: A, B, C, D, E, F.
Для большей понятности — внизу приведена таблица соответствия цифр трём системам счисления.
Запоминать соответствия цифр нет необходимости. В состав Windows любой версии входит программа «калькулятор» — calc.exe. Запустите её, переключитесь в программистский вид (Вид->Программист или Alt+3) и да пребудет с вами сила!
 Калькулятор программиста: HEX, DEC, OCT, BIN.
Калькулятор программиста: HEX, DEC, OCT, BIN.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Двоичная СС
шестнадцатеричная СС
Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:
A1416 = 10•16 2 + 1•16 1 + 4•16 = 10•256 + 1•16 + 4•1 = 2560 + 16 + 4 = 258010
Вычитание числа из строки и прибавление к строкам числа
В статье «Анализ вредоносной программы под Linux: плохое самодельное шифрование» рассматривается шифрование, которое основано на прибавлении или вычитании числа к символу строки (на основе позиции символов). Как я думаю вы уже поняли, используется аналогичный приём: берётся ASCII код символа и из этого числа делается вычитание или находиться сумма с ним, а затем полученное число опять переводят в ASCII символ.
Три системы счисления ; практическое использование.
Три системы счисления широко используются в программировании и отладке уже созданных программ.
Шестнадцатеричный (HEX) код удобен для современных процессоров, которые фактически развиваются на основе 16-ти разрядного процессора для персональных компьютеров Intel i8086. В исходных текстах программ практически всех языков программирования цифра обозначает по умолчанию число в десятичной системе счисления (DEC).
Десятичная система счисления более удобна (хотя и не всегда) при написании кода программ, шестнадцатеричная — неотъемлемая часть отладки, взлома, реверсивного программирования.
Двоичная система счисления (BIN) используется в основном при расстановке флагов определённых стилей объектов Windows (стили окон), но об этом попозже. Рассматривая 16 битное число в виде двоичного мы получаем великолепную возможность получить крохотный по размеру набор 16 флагов, где 1 — флаг установлен 0 — флаг снят (например, шестнадцатеричное число 4 000 соответствует двоичному 0100 0000 0000 0000 — установлен второй флаг, остальные сняты; шестнадцатеричное число 3000 соответствует двоичному числу 0011 0000 0000 0000 — установлены третий и четвёртый флаги, остальные сняты ).
Если мы хотим обозначить принадлежность числа к 16-тиричной системе счисления, то: 1. Ассемблер — добавляем к числу постфикс h (H), например: 100h = 256, 10H=16. Иногда для понимания того, что мы имеем дело с числом, в качестве префикса ставят 0 (ноль). 2. Си (С++) к числу добавляется суффикс 0x (0X).
Например: 0x100 = 100h = 0100h = 256, 0x10 = 10H = 010H = 16
ASCII и HTML
Если в HTML коде перед десятичным кодом ASCII символа поставить &#, то веб-браузер отобразит этот символ.
К примеру, если использовать ', то веб-браузер покажет ‘ (одинарную кавычку). Некоторые преобразователи строк внутри веб-приложения также могут конвертировать написание символов &#XX в их ASCII представления. Поэтому безобидная запись ' внутри веб-приложения может превратиться в одинарную кавычку, которая может нарушить SQL запрос.
Аналогично можно использовать &#x, после которой нужно указать код символа в шестнадцатеричной системе, например, ' также покажет кавычку. Для разделения символов друг от друга, используйте точку с запятой, например, ‘hi’
Многие программы понимают шестнадцатеричную запись, правда вид записи может различаться от конкретной программы и языка программирования.
В JavaScript шестнадцатеричные строки записываются в виде экранированной последовательности:
Можно записать код символов в восьмеричной системе счисления:
Аналогично Bash понимает такие строки:
И PHP их обрабатывает верно:
Шестнадцатеричный формат
Осуществить конвертацию из десятичного в шестнадцатеричный код (HEX — hexadecimal) можно только с использованием программ. Ручной метод основан на двойной конвертации. Для его реализации нужно перевести число, записанное в десятичной системе, в двоичный код, а затем в шестнадцатеричный.
Основанием является целочисленное значение, равное 16. Система состоит из арабских цифр от 0 до 9, а также букв, обозначающих конкретные значения: А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15. В автоматизированном режиме можно воспользоваться переводчиком шестнадцатеричного кода.
Необходимо отметить, что HEX применяется также в низкоуровневом программировании. Выбор этой системы счисления основан на решении в компьютерной технике применять такую единицу информации, как байт (состоит из 8 битов). Его удобно записывать двумя HEX-цифрами (от 0 до 255, т. е. #00 до #FF). Кроме того, шестнадцатеричный код в текст также конвертируется. Примером этому является кодировка Юникод, в которой для записи символа применяются четыре HEX-цифры. Цвет RGB-формата графического изображения также записывается с его помощью.
Способы записи
Существует несколько форм записи числа, представленного в HEX. Математическая форма выглядит таким образом: [DF5]<16>. Можно также найти запись, в которой вместо <16>стоит нижний индекс. Она применяется в информатике.
Запись отличается в языках программирования, поскольку у каждого из них различный синтаксис и правила написания кода. Основные формы представления HEX следующие:
- В С, С++ и похожих применяется префикс «0х».
- В Ассемблере после числа ставится латинская буква «h».
- В Pascal, Delfi, Basic используется символ «$».
- В HTML и CSS — «#».
- В Python — «0х».
Распространенная ошибка новичков заключается в том, что они неверно указывают HEX-числа. В результате компилятор языка выдает ошибку. Программисты рекомендуют основательно изучить синтаксис языка перед написанием приложений.
Алгоритм конвертации
Перевод в шестнадцатеричный код рекомендуется осуществлять с помощью специальных приложений (конвертеров кода). Если же их нет под рукой, то специалисты рекомендуют использовать специальный алгоритм:
- Выполнить конвертацию десятичной формы записи в двоичную по любому алгоритму.
- Распределить знаки на тетрады (по 4 штуки или четверичные группы). Если в какой-то группе их количество меньше 4, то дописывается в начале 0.
- Записать значения для каждой тетрады.
- Проверить результат.
Операции умножения, сложения, вычитания и деления сложны.
Они осуществляются только с помощью специальных программ или онлайн-сервисов.
Не следует путать четверичные с троичными группами, которые используются в восьмеричном коде.
Например, нужно перевести 118 в HEX-код.
Для этого следует воспользоваться описанным алгоритмом:
- Степенной метод, описанный выше: [118] <10>= [1110110]<2>.
- Распределение символов на тетрады (в старшем разряде нужно дописать 0): 0111 0110.
- Первое значение: 0 + 2 2 + 2 1 + 2 = 0 + 4 + 2 + 1 = [7]<16>.
- Второе: 0 + 2 2 + 2 1 + 0 = [6]<16>.
- Результат: [76]<16>.
В некоторых случаях нужно использовать буквы. Например, для перевода числа [11110111] <2>в HEX-код нужно также воспользоваться алгоритмом, разбивая его на тетрады следующим образом: 1111 0111. Первая группа равна 2 3 + 2 2 + 2 1 + 2 = [15] <10>= F<16>, а вторая — 0 + 2 2 + 2 1 + 2 = 7. Результирующая запись имеет такой вид: [11110111] <2>= [F7]<16>.
Таким образом, HEX-код получил широкое применение в IT-сфере, поскольку он очень удобен для записи массивов информации. Однако для его конвертации в ручном режиме нужно изучить двоичную систему счисления, а также основные алгоритмы преобразования.
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Двоичная восьмеричная шестнадцатеричная системы счисления
Двоичная система счисления
Для представления чисел в микропроцессоре используется двоичная система счисления .
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число x=anan-1..a1a0,a-1a-2…a-m запишется в двоичной системе счисления как
где ai — двоичные цифры (0 или 1).
Восьмеричная система счисления
В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:
Например, число 17510 в шестнадцатеричной системе счисления запишется как AF16. Действительно,
10·16 1 +15·16 0 =160+15=175
В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Двоично-восьмеричные и двоично-шестнадцатеричные преобразования
Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Три разряда двоичной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.
Пример: Преобразовать число 1101110,012 в восьмеричную систему счисления.
Объединяем двоичные цифры в триады справа налево. Получаем
Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:
Четыре разряда двоичной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.
Пример: Преобразовать число 1101110,112 в шестнадцатеричную систему счисления.
Объединяем двоичные цифры в тетрады справа налево. Получаем
Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом:
Шестнадцатеричная система счисления (информатика, 8 класс)
На уроках информатики в 8 классе изучается шестнадцатеричная система счисления. В IT-дисциплинах она применяется достаточно часто. Для декодирования числовой и буквенной информации в этот формат применяются специальные алгоритмы. Чтобы в них разобраться, необходимо иметь некоторые базовые понятия, а также уметь работать с двоичным и десятичным кодами.
- Общие сведения
- Виды систем счисления
- Использование в IT-сфере
- Методика конвертации
Общие сведения
Система счисления (СС) — набор некоторых символов, используемых для кодирования и декодирования информации различной формы. Любое представление имеет определенные свойства, которые и показывают основное отличие одной СС от другой. К ним относятся следующие:

- Алфавит.
- Мощность кодирования и декодирования.
- Величина основания.
- Способ получения.
Алфавитом называется набор цифр (иногда и литер), применяемых для построения заданного числового значения. В шестнадцатеричной системе счисления (HEX) применяются все цифры (от 0 до 9), а также буквы английского алфавита (А, B, C, D, E и F). Следует отметить, что для формирования HEX-величины используют шестнадцать знаков.
Специалисты рекомендуют составить таблицу шестнадцатеричной системы, состоящей из двух граф (HEX-кода и его расшифровки в десятичной форме). Ее также можно записать в виде обыкновенного списка:

- [1]<16>=1.
- [2]<16>=2.
- [3]<16>=3.
- [4]<16>=4.
- [5]<16>=5.
- [6]<16>=6.
- [7]<16>=7.
- [8]<16>=8.
- [9]<16>=9.
- [0]<16>=0.
- [A]<16>=10.
- [B]<16>=11.
- [C]<16>=12.
- [D]<16>=13.
- [E]<16>=14.
- [F]<16>=15.
Cледует отметить, что таблицу шестнадцатеричной системы представления величин специалисты рекомендуют записать на отдельном листе бумаге. Она должна быть постоянно перед глазами.

Мощность кодирования и декодирования данных определяется основанием СС. Чем оно больше, тем больше мощность формы представления чисел. Основанием называется определенный коэффициент, присутствующий в каждой СС. Он и дает название представлениям чисел, т. е. 5 — пятеричная, 6 — шестеричная, 14 — четырнадцатеричная и т. д.
Последняя характеристика (вид получения) показывает возможность кодирования числа в заданную форму представления. Она делится на два типа: прямой и косвенный. В первом случае операция конвертации происходит сразу. Например, для представления числа в двоичном коде его достаточно просто перевести по определенному алгоритму из десятичного формата в двоичную запись.
Иначе дело обстоит с 16-ричной СС, поскольку десятичный элемент нужно конвертировать в двоичный код, а затем уже в заданное hex-представление. Далее нужно рассмотреть классификацию СС.
Виды систем счисления
Системы представления делятся на два вида. К ним относятся следующие: позиционные и не зависящие от позиции символов. Первые включают в свой состав разрядную сетку. Последняя состоит из разрядов-цифр. Они стоят на определенном значимом месте, т. е. каждый из них имеет конкретное значение.
Чтобы был понятен принцип построения числа, необходимо рассмотреть значение «236». Величина состоит из разрядной сетки, в которую входят всего три компонента, а именно: единицы, десятки и сотни. Первое значение эквивалентно 6, второе — 3, а третье — 2. Расписать величину можно следующим образом: 6*10^0+3*10^1+2*10^2=6+30+200. В сумме элементы образуют значение 236.

Если поменять местами элементы, то получаются совершенно разные величины. Это говорит о том, что порядок цифр в разрядной сетке имеет очень важное значение. Исключением являются унарные формы представления чисел.
Унарной, или непозиционной, называется такая система счисления, в которой от положения символов не зависит величина. Например, в известном рассказе герой Робинзон Крузо вел подсчет дней, проведенных на необитаемом острове, при помощи обыкновенных палочек. Он записывал их в ряды, но при перестановке искомых элементов количество дней не менялось. Далее необходимо ознакомиться с применением HEX-чисел в программировании.
Использование в IT-сфере
HEX-форма записи величин получила широкое распространение в программировании с использованием регистров оперативной памяти и жесткого диска. На этих устройствах данные кодируются в определенном формате (шестнадцатеричная система в таблице специального типа). Чтобы проверить правильность работы программы, необходимо знать специальные методики конвертации.
Кроме того, необходимо знать порядок и правила выполнения арифметических операций, таких как сложение, вычитание, умножение и деление. Для этих целей применяются специальные приложения (калькуляторы). Однако бывают случаи, когда их нет под рукой. В этом случае необходимо выполнять конвертацию в десятичную систему представления величин. Следует выполнять необходимые операции, а затем переводить опять в HEX-код.

Следует отметить, что действия, позволяющие складывать или вычитать, можно выполнять без конвертации (прямо в HEX-формате). При этом нужно следить за переполнением разряда. Сложение шестнадцатеричных чисел можно осуществлять при помощи HEX-калькулятора. Если этого не делать, то можно сделать множество ошибок.
Вычитание шестнадцатеричных чисел выполняется по такому же принципу, что и сложение. Однако в этом случае нужно внимательно следить за убыванием старшего разряда. Умножать и делить нужно только при помощи специальных средств вычислительной техники, поскольку операции являются очень сложными.
Для примера можно сложить два числа, записанных в HEX-виде, а именно: F7 и 13. Первое число имеет высший разряд, значение которого равно F (максимальной цифре). При этом будет происходить переполнение разряда, т. к. F+1=1F. Если сложить величины, то получится такое число: 2F0. Начинающий IT-арифметик может потренироваться, придумывая примеры. Однако необходимо помнить, что любой результат должен проверяться при помощи калькулятора.
Методика конвертации
Методика перевода позволяет переводить десятичную форму в HEX-код. Чтобы выполнить данную операцию, нужно научиться переводить величины в двоичный код. Это делается при помощи такого алгоритма:

- Записать величину в десятичном формате: 131.
- Выполнить операцию деления на 2, записав соответствующий символ (0 — деление нацело, 1 — с остатком): 131/2=65 (1).
- 65/2=32 (1).
- 32/2=16 (0).
- 16/2=8 (0).
- 8/2=4 (0).
- 4/2=2 (0).
- 2/2=1 (остаток).
- Искомая величина (писать необходимо снизу вверх): [1000011]<2>.
Обратное преобразование является более простым. Для этого необходимо расписать величину по степеням с коэффициентами (0 — нет значения или 1 — величина присутствует), т. е. 1*2^0+1*2^1+0*2^2+0*2^3+0*2^4+0*2^5+1*2^6=1+2+128=131.
Для перевода в 16-ричную систему исчисления применяется алгоритм. Его реализация имеет следующий вид:

- Записать значение: 131.
- Конвертировать в двоичный код: 1000011. Можно не указывать фигурные скобки.
- Разложить величину, полученную во втором пункте, на тетрады по 4 компонента (сколько символов двоичного представления, столько и групп, деленных на двойку). Если при распределении не хватает элементов, то их можно дополнить нулями слева: (0100)(0011).
- Запись искомого числа: [43]<16>.
Обратная конвертация осуществляется также по некоторой методике. Она имеет такой вид:
- Написать HEX-число: [43]<16>.
- Разложить его по одному элементу: (4) (3).
- Перевести компоненты, полученные во втором пункте, в двоичный код: (0100)(0011).
- Конвертировать в десятичный формат: 131.
Следует отметить, что IT-специалисты настоятельно рекомендуют проверять результаты вычислений при помощи онлайн-калькуляторов для работы с двоичным и HEX-кодами. Если нет возможности выполнить проверку таким методом, то необходимо при получении результата выполнять на отдельном листе бумаги противоположную операцию, т. е. перевод в HEX-систему и обратно. В последнем случае вычисление должно соответствовать искомому значению в десятичной форме.
Таким образом, при выполнении различных арифметических операций с HEX-кодом необходимо знать методики конвертации и следовать рекомендациям специалистов в области IT-сферы.