Уравнение теплового баланса – формула, суть и примеры решений

Уравнение теплового баланса. КПД теплового процесса.

Рассмотрим замкнутую (теплоизолированную) систему.

Пусть в этой системе протекают процессы как с выделением теплоты, так и с поглощение тепла. Тогда учитывая, что по закону сохранения энергии, энергия не может ни откуда появится и не может ни куда исчезнуть, придем к выводу, что:

Суммарное количество теплоты выделяющееся в системе, равно суммарному количеству теплоты поглощенному в этой системе.

Тут в левой части равенства стоит суммарное количество теплоты выделяющееся в системе, а в правой части равенства суммарное количество теплоты поглощаемое в данной системе. Разные индексы стоящие в левой и правой частях равенства (n и k) свидетельствуют о том, что количество процессов идущих с поглощением и выделением энергии в общем случае может быть разным.

Приведенное равенство и называют уравнением теплового баланса.

По своей сути, уравнение теплового баланса есть следствие из закона сохранения энергии для процессов теплообмена в замкнутых системах.

Уравнение теплового баланса широко применяется при решении задач.

Пример решения задачи. Сколько кусочков льда, массой 10 г, взятых при температуре – 4ºС, нужно опустить в стакан с лимонадом находящимся в комнате при температуре 25ºС, чтобы его температура понизилась до 10ºС. Масса лимонада 200 г, удельную теплоёмкость лимонада считать равной удельной теплоёмкости воды. Потери энергии не учитывать.

Из условия задачи следует, что все количество теплоты выделяющееся при остывании лимонада от 25 до 10 градусов Цельсия, пойдет на нагревание льда от – 4ºС до нуля, плавление льда, и нагревание образовавшейся воды от нуля до 10ºС. Тогда можно составить уравнение теплового баланса, которое примет вид:

Q₁ = c_в m₁∆T₁– количество теплоты выделяющееся при охлаждении лимонада от 25 до 10 градусов Цельсия.

Q₂ = c_л n·m_л∆T₂– количество теплоты поглощенное при нагревании льда от – 4 до нуля.

Q₃ = λnm_л – количество теплоты поглощенное при плавлении льда.

Q₄ = c_в nm_л∆T₃– количество теплоты поглощенное при нагревании воды образовавшейся из льда от нуля до 10ºС

Подставим полученные выражения в уравнение теплового баланса:

В правой части уравнения вынесем искомую величину n за скобки:

подставив численные значения получим:

Так как кубики должны быть целыми, то ответ запишем так.

Ответ: Чтобы лимонад охладить от 25 до 10 градусов, в стакан нужно опустить 4 кубика льда.

В тех случаях, когда термодинамическая система не является замкнутой, а на практике чаще всего так и бывает, то неизбежны потери энергии. Физическая величина, показывающая процентную долю потерь энергии при теплообмене называется КПД теплового процесса.

На основании данного определения и уравнения теплового баланса можно получить уравнение:

где, в числителе стоит суммарное количество теплоты поглощенное в системе, а в знаменателе, суммарное количество теплоты выделяющееся в системе. Так как при теплообмене в реальных термодинамических системах неизбежны потери энергии в виде некоторого количества теплоты передающегося окружающей среде, то КПД теплового процесса всегда будет меньше 100%.

Например: КПД спиртовки равно 50%, это означает, что ровно половина количества теплоты, выделяющегося при сгорании спирта идет на нагревание того вещества, которое установлено на спиртовке, вторая половина выделяющегося количества теплоты передается окружающему воздуху, самой спиртовке и т.д.

Рассмотрим решение задачи:

Какую массу спирта нужно сжечь в спиртовке с КПД = 45%, что бы выпарить 100 г воды, взятой при температуре 20ºС?

∆T = 100 – 20 = 80ºC

Запишем уравнение для КПД теплового процесса.

,

Q₁ = cm₁∆T – количество теплоты поглощенное водой при нагревании от 20 до 100 градусов Цельсия.

Q₂ = Lm – количество теплоты поглощенное водой при испарении при температуре кипения.

Q₃ = qm₂ – количество теплоты выделяющееся при сгорании спирта.

Подставив полученные выражения в исходное уравнение, получим:

,

выразим из этого уравнения искомую величину m2:

.

Подставим численные значения и рассчитаем результат.

Ответ: Что бы выпарить 100 г, воды взятой при 20ºС, нужно сжечь примерно 20 г спирта.

Уравнение теплового баланса

Средняя оценка: 4.5

Всего получено оценок: 137.

Средняя оценка: 4.5

Всего получено оценок: 137.

Решение задач термодинамики заключается в нахождении неизвестных величин в процессе обмена теплом внутри рассматриваемой системы. Важнейшим этапом решения является составление уравнения теплового баланса. Далее с помощью обычных математических правил находятся неизвестные величины. Рассмотрим порядок построения этого уравнения.

Теплообмен в системе

В соответствии с положениями молекулярно-кинетической теории (МКТ), температура тела – это количественная характеристика энергии молекул тела. Каждая молекула обладает некоторой кинетической энергией, и средняя энергия молекулы пропорциональна температуре ($k$ – постоянная Больцмана):

В равновесном состоянии температура тела во всех точках системы одинакова, и, следовательно, средняя энергия также одинакова. При столкновениях молекулы обмениваются энергией, однако, в среднем, каждая молекула получает от соседних ту же энергию, что и отдает им.

Что произойдет, если система будет образована с телами разной температуры ?

Разная температура тел означает, что молекулы этих тел имеют разную среднюю энергию. При столкновениях молекул более энергичные молекулы горячего тела будут отдавать молекулам холодного тела гораздо больше энергии, чем молекулы холодного тела смогут отдать молекулам горячего. При этом сами молекулы горячего тела, отдавая энергию, теряют скорость (а значит, и температуру), а молекулы холодного тела – скорость увеличивают (а значит, и температуру).

Такой процесс передачи энергии молекул от горячего тела к холодному называется теплообменом.

Уравнение теплового баланса

Поскольку количество молекул пропорционально массе тела, а средняя энергия молекулы пропорциональна температуре, то количество тепла, отданное или принятое телом, пропорционально массе и разности температур до и после обмена:

При этом величина $Δt$ (а значит, и $Q$) будет положительна, если тело нагревается, и отрицательна, если тело охлаждается. Для окончательного нахождения количества тепла, принятого или отданного телом, необходимо ввести коэффициент пропорциональности, физический смысл которого состоит в том, что это количество энергии, необходимое, чтобы нагреть 1кг вещества на 1К. Данный коэффициент называется удельной теплоемкостью, обозначается латинской буквой «c», и имеет размерность в $Дж over кг × К$.

Рис. 2. Теплоемкость.

Таким образом, количество тепла, переданное n-му телу, равно:

$$Q_n = c_n m_n Δt_n$$

Поскольку система замкнута, то, согласно Закону сохранения энергии, общее количество энергии в системе остается постоянным. Теплообмен состоит лишь в том, чтобы энергия распределилась по системе равномерно. То есть, сумма количества тепла, переданного или принятого каждым телом в системе равна нулю:

В результате мы получили формулу уравнения теплового баланса. Подставив значения количества тепла, полученное или отданное каждым телом в системе, и решив получившееся уравнение, можно найти неизвестные величины.

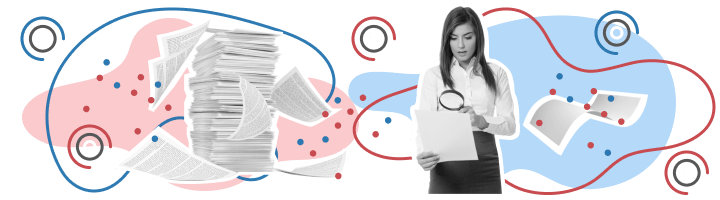
Подчеркнем, что система должна быть замкнутой – то есть теплоизолированной от внешнего мира. Обычно изоляция осуществляется с помощью специального теплообменного аппарата – калориметра.

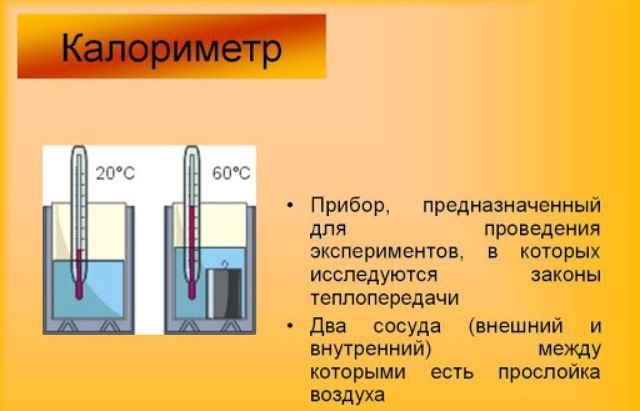Рис. 3. Калориметр.

Порядок составления уравнения теплового баланса

Для составления уравнения теплового баланса необходимо рассмотреть все тела в представленной системе. Каждое тело обладает определенной массой $m_n$ и теплоемкостью $c_n$.

Кроме того, в начальный момент каждое тело имело некоторую температуру $t_n$, а в после теплообмена во всей системе установилась новая температура $t_<рез>$. Следовательно, у каждого из тел надо определить разность температур $Δt_n = t_<рез>-t_n$ (эта величина будет положительной для нагреваемых тел, и отрицательной для охлаждаемых).

Подставляя эти три параметра (теплоемкость, массу и разность температур) в формулу количества тепла для каждого тела, получаем выражения для $Q_1$,$Q_2$,$Q_3$…, сумма этих составляющих по Закону сохранения энергии равна нулю. В результате имеем готовое уравнение теплового баланса для данной системы, из которого возможно определение неизвестной величины.

Что мы узнали?

Уравнение теплового баланса следует из закона сохранения энергии. Оно означает, что сумма тепла, полученная нагреваемыми телами равна сумме тепла, отданного охлаждаемыми, общее количество переданного тепла всеми телами равно нулю. Составив уравнение теплового баланса для системы, можно найти неизвестную величину.

Формулировка закона Бернулли и его математическое выражение

Обновлено: 02 Июня 2021

• Физическая сущность закона Бернулли
• Закон Бернулли как следствие закона сохранения энергии
• Проявление закона Бернулли в жизни

• Физическая сущность закона Бернулли
• Закон Бернулли как следствие закона сохранения энергии
• Проявление закона Бернулли в жизни

Принцип Бернулли заложил основы знания о движении жидкости, которое впоследствии перешло в самостоятельную науку — гидродинамику.

Физическая сущность закона Бернулли

Швейцарский математик и физик Даниил Бернулли родился в 1716 году в Голландии. За свою научную карьеру он получил звания Почетного члена Берлинской, Петербургской и Парижской академии наук, являлся членом Лондонского королевского общества. Главным научным трудом ученого является работа «Гидродинамика, или изъяснение сил и движений жидкости», опубликованная в 1733 году. Именно в этой книге были описаны физические основы механики жидкости.

Закон, названный его именем, Бернулли сформулировал во время работы в России, изучая взаимосвязь давления жидкости с ее скоростью. В математическом выражении он определяется уравнением Бернулли. Давайте разберемся, в чем состоит сущность закона.

Для начала определим, что закон Бернулли рассматривает движение потока несжимаемой идеальной жидкости, на которую действуют только силы тяжести и силы упругости.

Идеальная жидкость — это жидкость, в которой полностью отсутствует внутреннее трение и теплопроводность, ввиду чего, она лишена касательных напряжений между соседними слоями.

Подобная идеализация применяется при рассмотрении течения в гидродинамике. В законе Бернулли рассматривается стационарное течение жидкости — это движение слоев жидкости относительно друг друга и относительно ее самой, при котором скорость потока в некой конкретной точке не меняется, сохраняя свое постоянное значение. Давление при стационарном течении идеальной жидкости одинаково во всех поперечных сечениях трубки тока.

Для наглядности рассмотрим стационарное течение идеальной жидкости по трубе переменного сечения. В одном месте сечение этой трубки равно S1, а в другом — S2. При стационарном потоке через все сечения за определенный промежуток времени пройдет одинаковый объем жидкости, так как в ином случае, невозможность сжатия привела бы к ее разрыву. Таким образом, мы получаем уравнение неразрывности струи, определяющее соотношение между скоростью течения (v) и площадью сечения (S): S1v1=S2v2

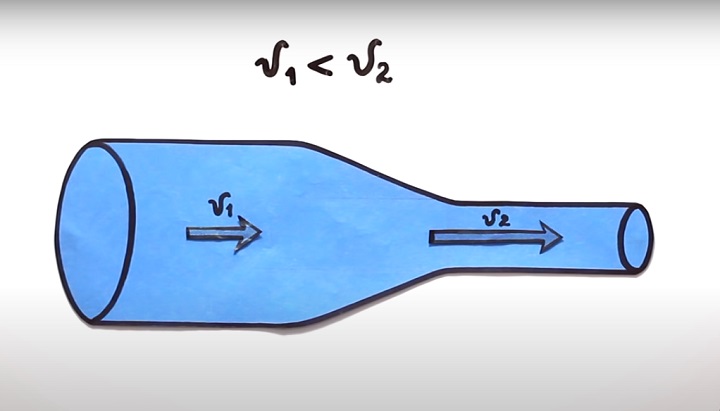
При этом скорость давление в сечении S1 меньше, чем в сечении S2. Как вы думаете, в каком из сечений скорость течения жидкости будет больше? Казалось бы, что по логике, скорость должна увеличиваться в том месте, где больше давление. Однако, согласно закону Бернулли, скорость увеличивается с уменьшением площади сечения. В этом-то и состоит парадоксальность принципа.

Закон Бернулли гласит, в тех участках течения жидкости или газа, где скорость больше, давление меньше, и наоборот, с увеличением давления жидкости, протекающей в трубе, скорость ее движения уменьшается. То есть, где больше скорость (v), там меньше давление (p).

Чтобы убедиться в этом, достаточно провести небольшой опыт из подручных средств. Возьмите два шара одного размера и подвесьте их так, чтобы между ними сохранялось небольшое расстояние. Подуйте между шарами или пустите воздух из фена. Шары вместо того, чтобы отдалиться, притянутся друг к другу. Это прямое следствие описанного закона, так как в том месте, куда вы дули, давление стало уменьшаться, а скорость шаров возросла, приблизив их друг к другу.

Закон Бернулли как следствие закона сохранения энергии

Из уравнения неразрывности следует, что в идеальной жидкости сумма статистического и динамического давлений и скоростного напора постоянна в любом сечении вдоль трубы. Являясь следствием закона сохранения, вывод уравнение Бернулли для элементарной струйки жидкости выглядит так:

rho) — плотность жидкости, (

v) — скорость потока, (

h) — высота, на которой находится рассматриваемый элемент жидкости, (

p) — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, (

g) — ускорение свободного падения.

При этом давление P — это статическое давление, которое получается в результате взаимодействия соседних слоев жидкости. Величина ρv2/2 — это динамическое давление, обусловленное движением жидкости, а ρgh — это давление, образованное массой вертикального столба жидкости высотой h, создаваемое силой тяжести.

Все эти величины имеют специальные обозначения, где h — высота положения или геометрический напор, P / ρ∙g — пьезометрический напор, v2 / 2g — скоростной напор.

Сумма трех слагаемых уравнения называется полным напором (H), то есть для идеальной жидкости при стационарном течении сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.

Для трубы, расположенной горизонтально, где величина высоты остается неизменной, уравнение Бернулли упрощается и выглядит так:

Проявление закона Бернулли в жизни

Закон Бернулли описывает одно из основных свойств гидравлики. Эффект, описанный швейцарским ученым, широко проявляется в природе и быту. Также широко его применение в технике. На основе принципа Бернулли работают такие приборы, как пульверизатор, водоструйный насос, аэрограф.

Чтобы понять механизм устройства, рассмотрим строение пульверизатора, которое включает в себя вертикальную трубку и горизонтальное сопло. Вертикальную трубку опускают в жидкость, в то время как по соплу пропускают воздух. Атмосферное давление, которое больше давления в струе воздуха, заставляет жидкость подниматься по трубке. Следовательно, при попадании в струю воздуха, происходит распределение жидкости.

В повседневной жизни закон Бернулли можно наблюдать, сидя у камина. При сильном ветре скорость воздушного потока возрастает, и, соответственно, падает давление. И так как давление воздуха в комнате выше, пламя, уходит вверх по дымоходу.

Это свойство используется и в аэродинамике для объяснения того, как возникает подъемная сила самолета или другого летательного аппарата, которое тяжелее воздуха.

В истории имеются и случаи отрицательного проявления закона. В 1912 году произошло столкновение океанского парохода «Олимпик» с гораздо меньшим по масштабам крейсером «Гаук», который плыл параллельно пароходу на расстоянии около 100 метров. Вдруг «Гаук» резко двинулся прямо на «Олимпик» и протаранил его силой удара. Так как два корабля были друг к другу слишком близко, скорость воды между ними стала больше, чем с другой стороны, вызвав дополнительную силу. Следовательно, вместо того, чтобы отдалиться, корабли притянулись друг к другу, что и стало причиной катастрофы.

В природе закон Бернулли проявляется во время урагана, когда из-за сильного ветра с домов слетают крыши. Это происходит, потому что скорость, с которой движется воздух вверху, очень большая, тогда как на чердаке она равна нулю. Как вы уже узнаете, там, где скорость потока больше, давление меньше, а там, где скорость меньше, давление больше. В результате образовавшейся разности давлений ураган и срывает кровлю.

Существует еще большое количество интересных примеров, изучение которых во многом упрощает усвоение закона Бернулли. Если вам нужно определить проявление закона в каком-то конкретном явление, обращайтесь к специалистам сервиса Феникс.Хелп, которые помогут решить задачу любой сложности.

Уравнение Бернулли

Основные уравнения гидродинамики – уравнение Бернулли и неразрывности позволяют установить взаимосвязь между параметрами плавно изменяющегося потока.

Уравнение Бернулли для потока идеальной жидкости

Рассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила – сила тяжести.

Выбреем два живых сечения , 1-1 в начале рассматриваемого участка, 2-2 – в конце.

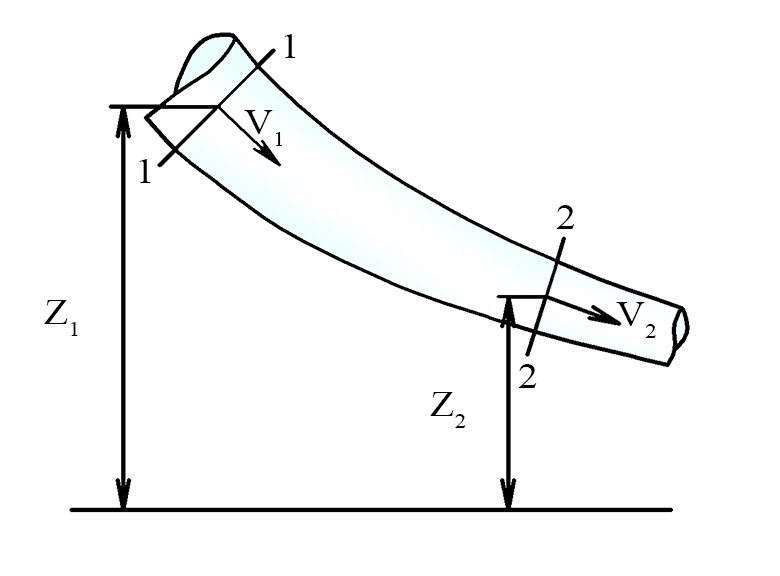
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.

Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.

Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор – величина постоянная.

Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:

Физический смысл уравнения Бернулли

Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:

• gz – удельная энергия положения,
• p/ρ – удельная энергия давления движущейся жидкости,
• V₁ 2 /2 – удельная кинетическая энергия жидкости,
• gz + p/ρ + V 2 /2 = Hg – полная удельная энергия движущейся идеальной жидкости.

Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.

Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.

Уравнение Бернулли для потока реальной вязкой жидкости

Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:

Н₁=Н₂ + Δh_{1 – 2} z₁ + p₁/ρg + V₁ 2 /2g = z₂ + p₂/ρg + V₂ 2 /2g + Δh_{1 – 2}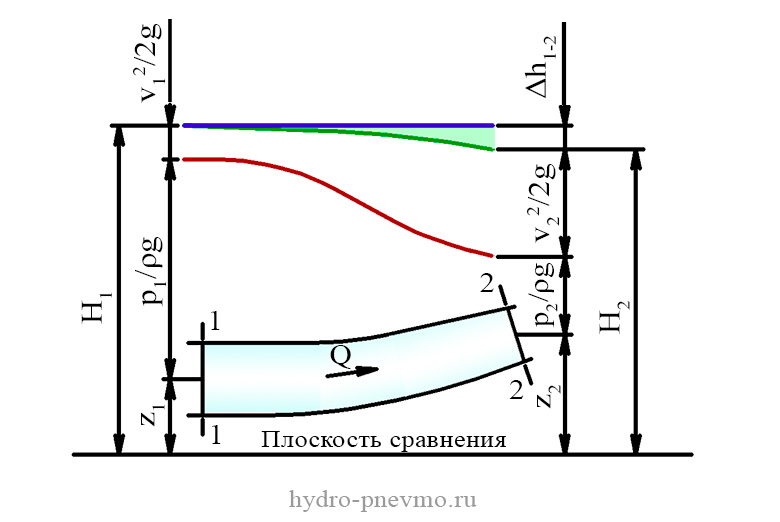

Уравнение Бернулли устанавливает связь между полными напорами потока жидкости на участке ограниченными сечениями 1-1 и 2-2. В соответствии с уравнением Бернулли полный напор потока Hi уменьшается от сечения 1-1 к сечению 2-2 на величину потерь напора (энергии) h_{1 – 2}, вызванных гидравлическими сопротивлениями участка.

Иллюстрация уравнения Бернулли

Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.

Уравнение Бернулли для горизонтальной трубы

Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:

Алгоритм решения задач с помощью уравнения Бернулли

Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:

1. Изобразить принципиальную гидравлическую схему системы
2. Провести общую для всего потока плоскость сравнения. Лучше всего провести ее самой нижней точки системы, например на уровне оси самого нижнего трубопровода, или не уровне жилкости самого нижнего резервуара.
3. Выбрать два (или несколько) живых сечения. Одно сечение выбирается в, том месте где параметры потока известны, другое там, где нужно определить неизвестные параметры (напрмер давление). Сечения следует выбирать только в тех местах где движение можно считать плавно изменяющимся. Нумеровать сечения следует в направлении движения жидкости.
4. Записать уравенение Бернулли для выбранных сечений.
5. При необходимости определить гидравлические потери напора на различных участка гидросистемы.
6. Вычислить неизвестные параметры, используя уранение Бренулли.

Основы гидравлики

Уравнение Бернулли – фундамент гидродинамики

Бернулли – вне всякого сомнения – имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

По закону сохранения энергии, изменение полной энергии E₂ – E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ – полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А – это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ – на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = – p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ – плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 – 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 – динамическим давлением, величина ρgh – гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением – давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора – полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ – коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая – прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито – Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ – площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие – µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .

Течение жидкости и уравнение Бернулли для новичков

• 12 января 2021 г.
• 6 минут
• 54 402

Как закон Всемирного Тяготения Ньютона действовал задолго до самого Ньютона, так и уравнение Бернулли существовало задолго до того, как родился сам Бернулли. Ему удалось лишь облечь это уравнение в наглядную форму, в чем его неоспоримая и огромная заслуга. Зачем мне уравнение Бернулли, спросите Вы, ведь я прекрасно жил и без него. Да, но оно может пригодиться Вам хотя бы на экзамене по гидравлике! Как говорится, «все не так уж плохо, если ты знаешь и можешь сформулировать уравнение Бернулли».

Кто такой Бернулли?

Даниил Бернулли – сын известного ученого Якоба Бернулли, швейцарский математик и физик. Жил с 1700 по 1782 годы, а с 1725 по 1733 трудился в Петербургской Академии наук. Помимо физики и математики Бернулли также изучал медицину наряду с Д’Аламбером и Эйлером считается отцом основателем математической физики. Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».

Д. Бернулли (1700-1782)

Идеальная жидкость и течение идеальной жидкости

Помимо известной нам материальной точки и идеального газа существует также идеальная жидкость. Какой-нибудь студент, конечно, может подумать, что эта жидкость – его любимое пиво или кофе, без которого невозможно жить. Но нет, идеальная жидкость – это жидкость, которая абсолютно несжимаема, лишена вязкости и теплопроводности. Тем не менее, такая идеализация дает вполне хорошее описание движения реальных жидкостей в гидродинамике.

Течением жидкости называется движение ее слоев относительно друг друга или относительно всей жидкости.

Помимо того есть разные режимы течения жидкости. Нас интересует тот случай, когда скорость потока в какой-то конкретной точке не меняется со временем. Такой поток называют стационарным. При этом скорость течения в различных точках стационарного потока может различаться.

Поток жидкости– совокупность частиц движущейся жидкости.

Поток жидкости

Вывод уравнения Бернулли

Но как описать движение жидкости? Для этого нам нужно знать вектор скорости частиц, точнее зависимость его от времени. Совокупность скоростей в разных точках потока дает поле вектора скорости.

Рассмотрим стационарное течение жидкости по трубке. В одном месте сечение этой трубки равно S1, а в другой – S2. При стационарном потоке через оба сечения за одинаковый промежуток времени пройдет одинаковое количество жидкости.

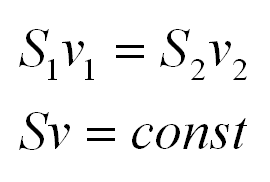
Данное уравнение – уравнение неразрывности струи.

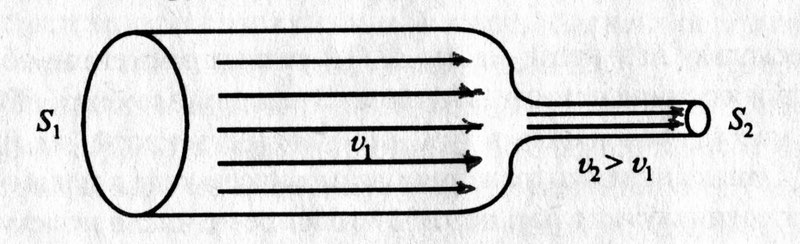К выводу уравнения Бернулли

Узнав его, Бернулли решил установить связь между давлением и скоростью жидкости в разных сечениях. Полное давление – это сумма статистического (обусловлено потенциальной энергией жидкости) и динамического давлений (обусловлено кинетической энергией). Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:

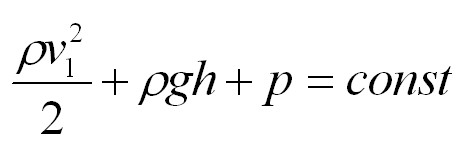
Смысл уравнения Бернулли

Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.

Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.

Уравнение Бернулли – основные понятия, формулы и определения с примерами

Уравнение Бернулли:

При изучении статики жидкости мы выяснили, как распределяется давление в неподвижной жидкости. А как распределяется давление в движущейся жидкости? Выясним это экспериментально. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены открытые сверху манометрические трубочки (рис. 190). Отверстия в стенке практически не влияют на распределение давления в жидкости. При стационарном течении жидкость в манометрических трубочках поднимется на определенную высоту. Высота столба жидкости от некоторого уровня показывает разность между давлением жидкости в трубке в месте расположения отверстий и атмосферным давлением. Опыт показывает, что в широких местах трубки давление больше, чем в узких. Но по уравнению неразрывности, чем больше сечение трубки, тем меньше скорость течения жидкости. Следовательно, можно сделать вывод:
при стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и, наоборот, меньше в тех местах, где скорость течения больше.

Эта зависимость была установлена швейцарским физиком Д. Бернулли и называется законом Бернулли.

Качественное объяснение этого закона основано на уравнении неразрывности и втором законе Ньютона.

Выделим небольшой объем жидкости, который движется вдоль трубки. При переходе из широкой части трубки в узкую его скорость увеличивается от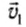

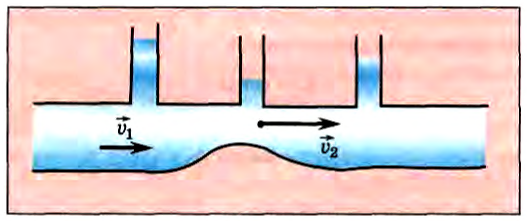
Рис. 190

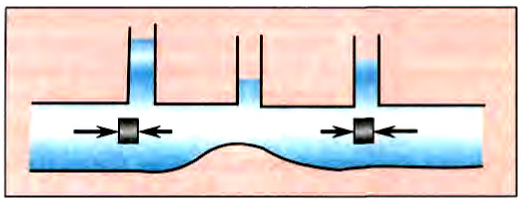
Рис. 191

Д. Бернулли также установил зависимость давления идеальной жидкости от скорости ее стационарного течения и перепада высоты.

Выделим в потоке идеальной жидкости тонкую трубку тока, а в ней некоторый объем между сечениями AB и CD (рис. 192).

Рис. 192

Пусть площадь поперечного сечения, давление и модуль скорости потока в сечении AB соответственно равны S₁, p_l, υ₁, а в сечении CD — S₂, p₂, υ₂. Под действием сил давления 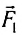и 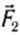и силы тяжести выделенный объем жидкости за малый промежуток времени Δt сместится вправо и займет положение между сечениями A₁B₁ и C_lD_l. Силы давления 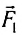и 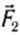совершат работу:
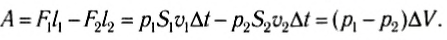(1)

Существенно, что при стационарном течении жидкости энергия объема жидкости, заключенного между сечениями A₁B₁ и CD (см. рис. 192), остается неизменной. Все происходит так, как если бы жидкость, занимавшая объем ABB₁A₁, переместилась и заняла объем CDC₁D₁. Поэтому достаточно учесть лишь изменение энергии жидкости, переходящей из области ABA₁B₁ в область CDD₂C₂. При этом изменяются кинетическая энергия К и потенциальная энергия П. Изменение полной энергии W выделенного объема жидкости равно: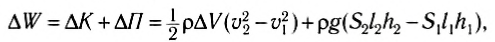

где h₁ и h₂ — высоты расположения соответствующих объемов (см. рис. 192).

Поскольку мы рассматриваем идеальную жидкость, в которой нет сил трения, то в данном случае можно использовать закон сохранения энергии в форме ∆W = А. C учетом этого получаем: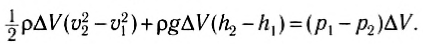

После сокращения на ΔV соберем величины с одинаковыми индексами в одной части равенства.
В результате получим: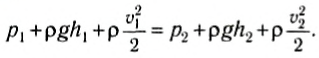

Мы произвольно выбирали поперечные сечения трубки тока. Поэтому выражение

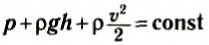является постоянным в любом сечении трубки тока. Это и есть уравнение Бернулли.

Выясним физический смысл входящих в формулу (3) величин. Величину
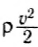можно записать:

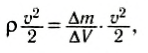
где ∆m — масса выделенного малого объема жидкости, ΔV— его объем. Следовательно, 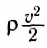есть кинетическая энергия единичного объема и называется плотностью кинетической энергии. Аналогично можно показать, что pgh — плотность потенциальной энергии.

Итак, сумма давления и плотностей кинетической и потенциальной энергий (трехчлен Бернулли) при стационарном течении идеальной жидкости остается постоянной для любого сечения трубки тока.

В уравнении (3) площадь поперечного сечения отсутствует. Следовательно, можно выбрать очень тонкую трубку тока, которая фактически представляет собой линию тока. Поэтому уравнение Бернулли часто формулируют так:
при стационарном течении идеальной жидкости трехчлен Бернулли 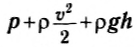постоянен вдоль любой линии тока.

Используя уравнение Бернулли, можно объяснить ряд интересных явлений и решить многие задачи.

Так, при горизонтальном течении жидкости плотность потенциальной энергии постоянна и уравнение Бернулли примет вид: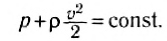

Отсюда следует, что в тех точках пространства, где скорость больше, давление меньше. Это подтверждается опытом, описанным в начале этого параграфа. C помощью уравнения Бернулли можно найти скорость истечения жидкости из отверстия, расположенного в сосуде на глубине h относительно поверхности жидкости (рис. 193). Выделим в сосуде линию тока 1—2, как показано на рисунке. Пусть атмосферное давление p₀. Записав уравнение Бернулли для точек 1 и 2, получим:
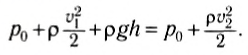(4)

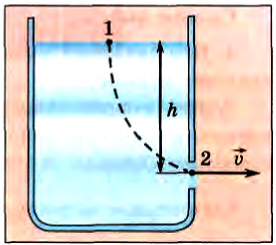
Рис. 193

Считая площадь отверстия малой по сравнению с площадью поперечного сечения сосуда, можно пренебречь скоростью опускания уровня жидкости в сосуде, положив υ₁ = 0. Тогда из формулы (4) следует формула Торричелли:

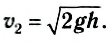
Истечение происходит с той же скоростью, какую имело бы тело при свободном падении с высоты h.

Зависимость давления в жидкости и газе от их скорости лежит в основе принципа действия многих устройств и приборов. На рисунке 194 изображена схема устройства водоструйного насоса. Струя воды подается в трубку А, имеющую на одном конце сужение. По сужению вода течет с большей скоростью. Из-за этого давление в струе в этом месте оказывается меньше атмосферного, воздух из сосуда всасывается в струю через трубку В и удаляется вместе с водой.

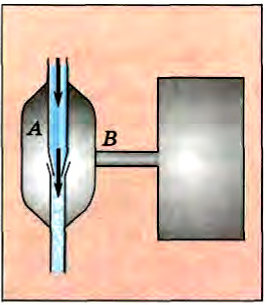
Рис. 194

На рисунке 195 изображен простейший пульверизатор, состоящий из двух трубок, расположенных перпендикулярно. Через горизонтальную трубку продувается воздух. В узкой части струи при выходе из трубки давление меньше атмосферного. Жидкость поднимается по вертикальной трубке из-за разности давлений и распыляется струей воздуха. Точно так же работают различные краскораспылители.

Рис. 195

Главные выводы:

1. При движении жидкости в тех местах, где скорость течения больше, давление меньше.
2. При стационарном течении идеальной жидкости сумма давления и плотности кинетической и потенциальной энергий жидкости постоянна вдоль линии тока.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.