Презентация “«История изобретения паровой машины»” по физике – проект, доклад
Презентацию на тему “«История изобретения паровой машины»” можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад – нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации

История изобретения паровой турбины.

тепловой двигатель внешнего сгорания, преобразующий энергию нагретого пара в механическую работу возвратно-поступательного движения поршня, а затем во вращательное движение вала. В более широком смысле паровая машина — любой двигатель внешнего сгорания, который преобразовывает энергию пара в механическую работу.

На первых парах

Девятнадцатый век не зря называли веком пара. С изобретением паровой машины произошел настоящий переворот в промышленности, энергетике, транспорте. Появилась возможность механизировать работы, ранее требовавшие слишком много человеческих рук.

Расширение объемов промышленного производства поставило перед энергетикой задачу всемерного повышения мощности двигателей. Однако первоначально вовсе не высокая мощность вызвала к жизни паровую турбину.

Гидравлическая турбина как устройство для преобразования потенциальной энергии воды в кинетическую энергию вращающегося вала известна с глубокой древности. У паровой турбины история столь же долгая, ведь одна из первых конструкций известна под наименованием “турбины Герона” и датируется первым столетием до нашей эры. Однако сразу заметим – вплоть до XIX века турбины, приводимые в движение паром, являлись скорее техническими курьезами, игрушками, чем реальными промышленно применимыми устройствами.

И только с началом индустриальной революции в Европе, после широкого практического внедрения паровой машины Д. Уатта, изобретатели стали присматриваться к паровой турбине, так сказать, “вплотную”.

Создание паровой турбины требовало глубокого знания физических свойств пара и законов его истечения. Изготовление ее стало возможным только при достаточно высоком уровне технологии работы с металлами, поскольку потребная точность изготовления отдельных частей и прочность элементов были существенно более высокими, чем в случае паровой машины.

Однако время шло, техника совершенствовалась, и час практического применения паровой турбины пробил. Впервые примитивные паровые турбины были использованы на лесопилках в восточной части США в 1883-1885 гг. для привода дисковых пил.

Изобретение Карла Густава Патрика Лаваля (1845—1913)
Паровая турбина Лаваля представляет собой колесо с лопатками. Струя пара, образующегося в котле, вырывается из трубы (сопла), давит на лопасти и раскручивает колесо. Экспериментируя с разными трубками для подачи пара, конструктор пришёл к выводу, что они должны иметь форму конуса. Так появилось применяемое до настоящего времени сопло Лаваля (патент 1889 г.). Это важное открытие изобретатель сделал, скорее, интуитивно; понадобилось ещё несколько десятков лет, чтобы теоретики доказали, что сопло именно такой формы даёт наилучший эффект.

Чарльз Алджернон Парсонс (1854— 1931)
Заниматься турбинами начал в 1881 г., а уже спустя три года ему выдали патент на собственную конструкцию: Парсонс соединил паровую турбину с генератором электрической энергии. С помощью турбины стало возможно вырабатывать электричество, и это сразу повысило интерес общества к паровым турбинам. В результате 15-летних изысканий Парсонс создал наиболее совершенную по тем временам реактивную многоступенчатую турбину. Он сделал несколько изобретений, повысивших экономичность этого устройства (доработал конструкцию уплотнений, способы крепления лопаток в колесе, систему регулирования числа оборотов).

Огюст Рато (1863—1930)
Создал комплексную теорию турбомашин. Он разработал оригинальную многоступенчатую турбину, которая с успехом демонстрировалась на Всемирной выставке, проходившей в столице Франции в 1900 г. Для каждой ступени турбины Рато рассчитал оптимальное падение давления, что обеспечило высокий общий коэффициент полезного действия машины.

Гленн Кертис (1879—1954)
В его машине скорость вращения турбины была ниже, а энергия пара использовалась полнее. Поэтому турбины Кертиса отличались меньшими размерами и более надёжной конструкцией. Одна из главных областей применения паровых турбин — двигательные установки кораблей. Первое судно с паротурбинным двигателем — «Турбиния», — построенное Парсонсом в 1894 г., развивало скорость до 32 узлов (около 59 км/ч).

Применение паровых турбин

Экспериментальный паровой грузовик НАМИ-012 на базе ЯАЗ-200 мог работать на угле, торфе и дровах

Американский паровик Doble выпускался в крайне ограниченных количествах: с 1923 по 1932 годы было изготовлено всего 42 экземпляра. Образец на иллюстрации датирован 1929 годом.

Паромобили марки Brooks покидают конвейер фабрики в Стратфорде, Онтарио, 1926 год.

В настоящее время о паровом двигателе почти никто не вспоминает. Хотя всплеск интереса в послевоенные годы был — в связи с созданием компактных турбинных двигателей.
Первые паровые машины в мире: истории их изобретения


Паровая машина стала первым механическим двигателем, для которого нашлось широкое практическое применение. Первые поршневые паровые машины начали вначале применяться на фабричном производстве, а позднее их смогли соединить с колёсами и получить самодвижущиеся машины:
- пароходы;
- паровозы;
- тракторы;
- автомобили.
История изобретения паровой машины
Основной принцип действия любой паровой машины заключается в том, что энергия горячего пара преобразуется в механическую энергию, которая может быть:
- возвратно-поступательной;
- вращательной.
А полученная механическая энергия может уже использоваться для полезных целей. Принцип работы паровой машины был понятен ещё древним грекам, но в тёмные века люди о нём прочно забыли. Вновь интерес к этой проблеме возродился только в 17-м веке. Итальянец Джованни Бранка в 1629 году предложил модель собственной паровой турбины. Но из-за недопустимо больших потерь энергии эта первая паровая машина в мире практического применения не нашла.
Паровая машина Дени Папена
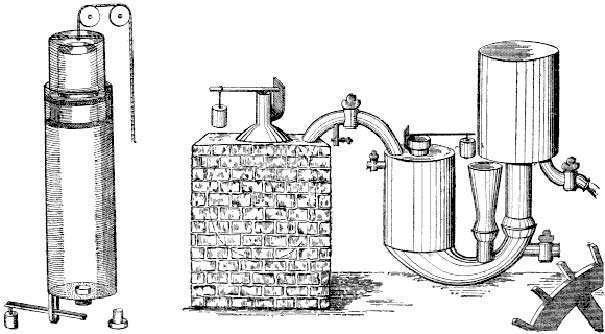 Этот француз – медик по образованию, переехал в 1675 году в Англию, где отметился целым рядом изобретений. Так, им изобретён «папенов котёл» – прообраз современной пароварки. Папен смог заметить взаимосвязь между ростом давления и температуры кипения жидкости. Он смог соорудить герметичный котёл, где поддерживалось повышенное давление. В результате этого вода в нём закипала при повышенной температуре, а продукты стало возможно готовить при температуре выше 100 градусов, что ускоряло процесс приготовления пищи.
Этот француз – медик по образованию, переехал в 1675 году в Англию, где отметился целым рядом изобретений. Так, им изобретён «папенов котёл» – прообраз современной пароварки. Папен смог заметить взаимосвязь между ростом давления и температуры кипения жидкости. Он смог соорудить герметичный котёл, где поддерживалось повышенное давление. В результате этого вода в нём закипала при повышенной температуре, а продукты стало возможно готовить при температуре выше 100 градусов, что ускоряло процесс приготовления пищи.
Накануне переезда в Туманный Альбион Папен изобрёл пороховой двигатель. Сгорающий в цилиндре порох толкал поршень. Образовавшиеся пороховые газы удалялись через клапан, а оставшиеся остывали, благодаря чему в цилиндре возникало лёгкое разрежение, и давление атмосферы возвращало на место поршень.
По подобному же принципу Папен создал в 1698 году аналогичный двигатель, но уже на воде. Это фактически была первая паровая машина.
Несмотря на то, что сама идея сулила немалые выгоды, своему автору она дивидендов не принесла. Дело в том, что несколько раньше Сейвери (английский механик) запатентовал свой паровой насос, что было на тот момент единственным способом применения для паровой машины. Так вышло, что изобретатель первой паровой машины Дени Папен умер в 1714 году в Лондоне, будучи бедным и одиноким.
Машина Томаса Ньюкомена
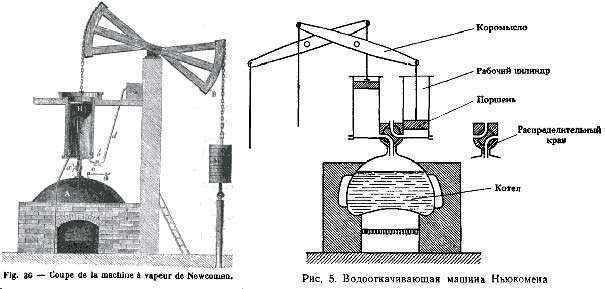 Больших барышей смог добиться этот предприимчивый англичанин. Ему было 35 лет, когда создавалась машина Папена. Ньюкомен тщательно изучил наследие Папена и Сейвери и отметил недостатки обеих моделей, а сильные идеи взял на вооружение. Сотрудничая со специалистом по водопроводам и стеклу Д. Калли, Ньюкомен создал к 1712 году первую свою модель, продолжив историю создания паровых машин. Её принципиальная работа выглядела так:
Больших барышей смог добиться этот предприимчивый англичанин. Ему было 35 лет, когда создавалась машина Папена. Ньюкомен тщательно изучил наследие Папена и Сейвери и отметил недостатки обеих моделей, а сильные идеи взял на вооружение. Сотрудничая со специалистом по водопроводам и стеклу Д. Калли, Ньюкомен создал к 1712 году первую свою модель, продолжив историю создания паровых машин. Её принципиальная работа выглядела так:
- в конструкции был вертикальный цилиндр с поршнем (от Папена);
- пар генерировался в отдельном котле, который действовал по принципу изобретения Сэйвери;
- герметичность паровому цилиндру обеспечивала обтягивающая поршень кожа.
Нагнетая давление, устройство Ньюкомена поднимало из шахт воду. Но оно было очень громоздкое и чрезвычайно прожорливое на уголь. Но эти недостатки не помешали полувековой эксплуатации данного изобретения на шахтах. Благодаря нему стало возможно реанимировать ранее заброшенные из-за подтопления грунтовой водой шахты. Но поскольку его машина была компиляцией ранних изобретений, то Ньюкомен патента на неё получить не смог.
Машина Уатта
Решающий шаг смог сделать британец Джеймс Уатт, благодаря усилиям которого появилась достаточно мощная и компактная первая поршневая паровая машина. Будучи механиком университета Глазго, Уатт в 1763 году взялся за починку паровой машины Ньюкомена. В процессе ремонта он придумал способ сокращения её прожорливости – её цилиндр нужно было поддерживать в нагретом состоянии.
Но требовалось решить ещё проблему конденсации пара. Решение он уловил, проходя мимо прачечных, из-под крышек котлов которых валили пар. Он сообразил, что пар является газом, который и следует запустить в цилиндр с пониженным давлением. Он добился герметичности системы поршень-цилиндр путём обмотки первого промасленной пеньковой верёвкой, после чего стал возможным отказ от атмосферного давления – заметный шаг вперёд.
В 1769 году Уатт запатентовал паровую машину, в которой температура пара и важнейших деталей была одинаковой.
Видео о первой паровой машине Джеймса Уатта
Но в жизни Уатту везло меньше, и патент ему пришлось заложить за долги. Через 3 года он познакомился с богатым промышленником Мэттью Болтоном, который выкупил для Уатта его патенты. Под его опекой Уатт вернулся к работе. Уже в 1773 году новая модель Уатта на испытаниях продемонстрировала гораздо меньшее потребление угля, чем требовали её предшественники. А ещё через год Англия начала промышленный выпуск машин Уатта. В 1781 году Уатт запатентовал паровую машину, которая приводила в действие промышленные станки. Ещё чуть позднее эти же технологии стали использоваться для движения пароходов и поездов, что станет подлинной технической революцией.
Паровая машина Ползунова
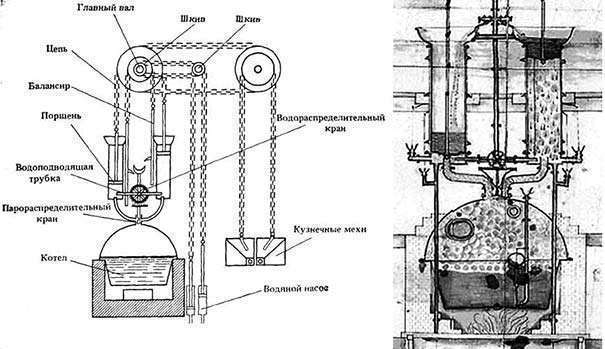 Нам не менее дорог Иван Ползунов – русский изобретатель первой паровой машины, которая была способна приводить в действие многие рабочие механизмы. Причём, сделал он это изобретение раньше Уайта – в 1763 году, работая на алтайских горнорудных заводах. Он ознакомил со своим проектом начальника заводов, а тот получил из столицы добро на сборку агрегата. Ползунову приказали построить большую машину.
Нам не менее дорог Иван Ползунов – русский изобретатель первой паровой машины, которая была способна приводить в действие многие рабочие механизмы. Причём, сделал он это изобретение раньше Уайта – в 1763 году, работая на алтайских горнорудных заводах. Он ознакомил со своим проектом начальника заводов, а тот получил из столицы добро на сборку агрегата. Ползунову приказали построить большую машину.
Эта работа заняла 21 месяц, но когда она была почти готова, болевший чахоткой изобретатель умер, не дожив нескольких дней до её первых испытаний. Паровая машина Ползунова могла работать беспрерывно и в автоматическом режиме. Это было доказано в результате испытаний, проведённых в 1766 году учениками Ползунова. А через месяц машина уже начала трудиться, не только окупив все затраты на своё создание, но и принеся владельцам прибыль.
Как Вы считаете, кого можно назвать первым изобретателем паровой машины? Расскажите об этом в комментариях.
Электрический ток. Закон Ома для цепей постоянного и переменного тока.
Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.
Начнём с терминологии.
Электрический ток – это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи – физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление – это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Теперь можно переходить к закону Ома.
Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.
Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,
 где
где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].
Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.
Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P(Вт) = U(В)×I(А) = I 2 (А)×R(Ом) = U 2 (В)/R(Ом)
Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.
Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.
Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.
ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.
Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.
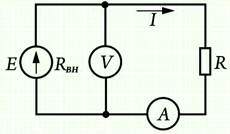
Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр .
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название – закон Ома для полной цепи:
I=U/(R+r) .
Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду: 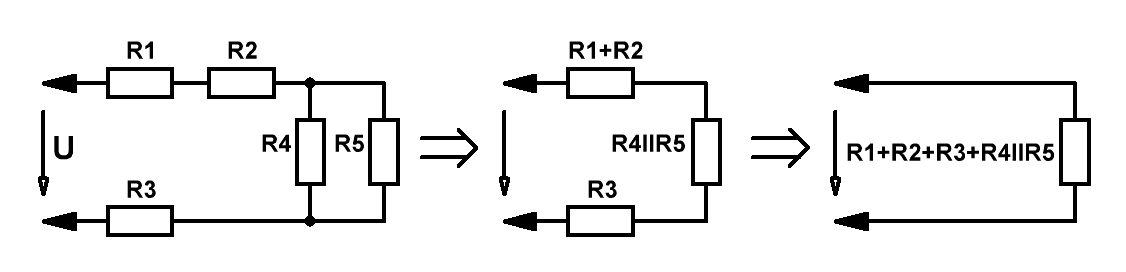
Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/Rll = 1/R4+1/R5 .
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.
Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока – под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.
А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.
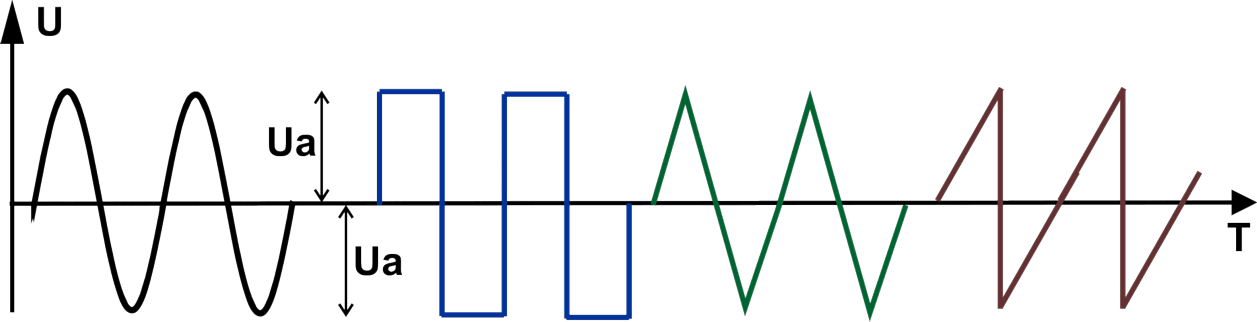
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов – это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.
Рассчитываем действующее значение напряжение интересующей нас формы:
Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.
С этим разобрались!
Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:
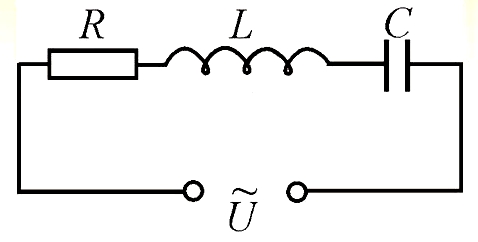
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид: 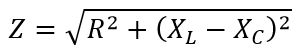
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: XC = 1/(2πƒС) , XL = 2πƒL .
Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента – необходимо указать значение частоты f !
КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.
Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания. 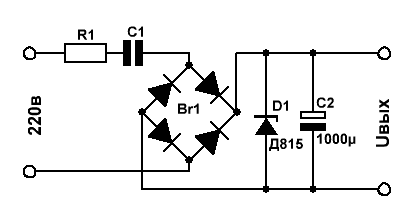
Токозадающими цепями в данной схеме являются элементы R1 и С1.
Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом – 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в – 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 – 30 Ом, С1 – 1 Мкф, частотой сети f – 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет – надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости – 3,18 Мкф, при котором Z = 1,04кОм.
Всё – закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!
Сила тока: что это такое, формула, в чем измеряется сила тока?
Электрический ток
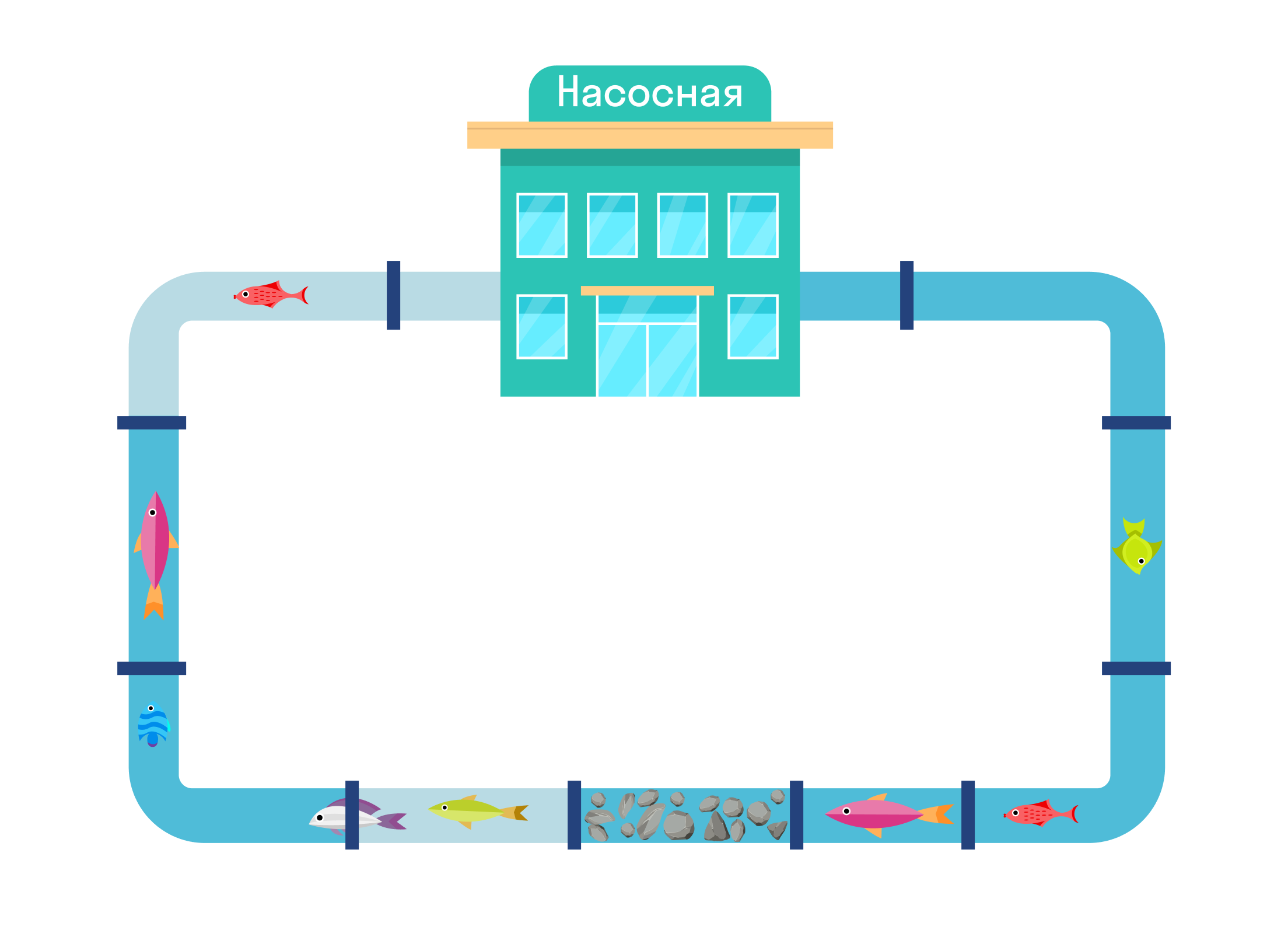
По проводам течет электрический ток. Причем он именно «течет», практически как вода. Представим, что вы — счастливый фермер, который решил полить свой огород из шланга. Вы чуть-чуть приоткрыли кран, и вода сразу же побежала по шлангу. Медленно, но все-таки побежала.
Сила струи очень слабая. Потом вы решили, что напор нужен побольше и открыли кран на полную катушку. В результате струя хлынет с такой силой, что ни один помидор не останется без внимания, хотя в обоих случаях диаметр шланга одинаков.
А теперь представьте, что вы наполняете два ведра из двух шлангов. У одного из них напор сильнее, у другого слабее. Быстрее наполнится то ведро, в которое льется вода из шланга с сильным напором. Все дело в том, что объем воды за равный промежуток времени из двух разных шлангов тоже разный. Иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.
Если мы возьмем проводник с током, то будет происходить то же самое: заряженные частицы будут двигаться по проводнику, как и молекулы воды. Если больше заряженных частиц будет двигаться по проводнику, то «напор» тоже увеличится.
- Электрический ток — это направленное движение заряженных частиц.
Что представляет собой ток
Перейдём к определению, что такое электрический ток!
Электрический ток — это направленное движение электрически заряженных частиц (в нашем случае это-рыбки) под воздействием электрического поля (в нашем случае это вода).
Сила тока
Сразу возникает потребность в величине, которой мы будем «напор» электрического тока измерять. Такая, чтобы она зависела от количества частиц, которые протекают по проводнику.
Сила тока — это физическая величина, которая показывает, какой заряд прошел через проводник.
Сила тока измеряется в Амперах. Единица измерения выбрана не просто так.
Во-первых, она названа в честь физика Андре-Мари Ампера, который занимался изучением электрических явлений. А во-вторых, единица этой величины выбрана на основе явления взаимодействия двух проводников.

Здесь аналогии с водопроводом провести, увы, не получится. Шланги с водой не притягиваются и не отталкиваются вблизи друг друга (а жаль, было бы забавно).
Когда ток проходит по двум параллельным проводникам в одном направлении, проводники притягиваются. А когда в противоположном направлении (по этим же проводникам) — отталкиваются.

За единицу силы тока 1 А принимают силу тока, при которой два параллельных проводника длиной 1 м, расположенные на расстоянии 1 м друг от друга в вакууме, взаимодействуют с силой 0,0000002 Н.
Найти силу тока в цепи, если за 2 секунды в ней проходит заряд, равный 300 мКл.
Возьмем формулу силы тока
I = 300 мКл / 2 с = 150 мА
Ответ: сила тока в цепи равна 150 мА
Основные единицы измерения силы тока
В качестве основной единицы измерения силы тока используют ампер (краткое обозначение – А). Ампер, получивший свое название по имени ученого физика Анри Ампера, входит в Международную систему единиц (СИ).
Если через поперечное сечение в течение 1 секунды проходит 1 кулон электричества, то сила тока в этом проводнике равна одному амперу. Как вспомогательные единицы применяются:
- миллиамперы (ма), одна тысячная или 10-3 ампер;
- микроамперы (мкА), одна миллионная или 10-6 ампер.
Сила тока является важным параметром, знание которого поможет в выборе кабелей с оптимальным для планируемой нагрузки размером сечения.
Сила тока — обозначение и базовые формулы
В формулах при расчете такого параметра, как сила тока, обозначение его величины с помощью буквы «I» является общепринятым. Основная формула выглядит как I=q/t, где q – количество электричества, а t – временной отрезок.
Также для расчета силы тока можно использовать такие параметры, как:
- фактическое напряжение (U);
- мощность (P).
В этом случае применяется формула I= P/U. Получение силы тока расчетным методом актуально в тех случаях, когда невозможно применение измерительных приборов, например, на этапе проектирования электросетей.
Закон Ома
Из этой статьи вы поняли, что является электрическим током. Но как же нам вычислить силу тока.
Вы видите формулу, по которой вычисляется ток для участка цепи.

I-ток, Ампер
U-напряжение, Вольт
R-сопротивление, Ом
Чтобы вычислить силу тока, необходимо напряжение разделить на сопротивление.
Дорогие читатели, подписывайтесь на обновления блога и в следующих статьях я расскажу, что такое напряжение и сопротивление!
Сила тока и сопротивление
Давайте еще раз глянем на шланг с водой и зададим себе вопросы. От чего зависит поток воды? Первое, что приходит в голову – это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу – это элементарно.
Теперь такой вопрос: как можно увеличить количество электронов через площадь поперечного сечения?
Первое, что приходит на ум – это увеличить давление. В этом случае скорость потока воды увеличится, но ее много не увеличишь, так как шланг порвется как грелка в пасти Тузика.
Второе – это поставить шланг бОльшим диаметром. В этом случае у нас количество молекул воды через поперечное сечение будет проходить больше, чем в тонком шланге:
Все те же самые умозаключения можно применить и к обыкновенному проводу. Чем он больше в диаметре, тем больше он сможет “протащить” через себя силу тока. Чем меньше в диаметре, то желательно меньше его нагружать, иначе его “порвет”, то есть он тупо сгорит. Именно этот принцип заложен в плавких предохранителях. Внутри такого предохранителя тонкий проводок. Его толщина зависит от того, на какую силу тока он рассчитан.
Как только сила тока через тонкий проводок предохранителя превысит силу тока, на которую рассчитан предохранитель, то плавкий проводок перегорает и размыкает цепь. Через перегоревший предохранитель ток уже течь не может, так как проводок в предохранителе в обрыве.
сгоревший плавкий предохранитель
Поэтому, силовые кабели, через которые “бегут” сотни и тысячи ампер, берут большого диаметра и стараются делать из меди, так как ее удельное сопротивление очень мало.
Сила тока в проводнике
Очень часто можно увидеть задачки по физике с вопросом: какая сила тока в проводнике? Проводник, он же провод, может иметь различные параметры: диаметр, он же площадь поперечного сечения; материал, из которого сделан провод; длина, которая играет также важную роль.
Да и вообще, сопротивление проводника рассчитывается по формуле:
формула сопротивления проводника
Таблица с удельным сопротивлением из разных материалов выглядит вот так.
таблица с удельным сопротивлением веществ
Для того, чтобы найти силу тока в проводнике, мы должны воспользоваться законом Ома для участка цепи. Выглядит он вот так:
У нас есть медный провод длиной в 1 метр и его площадь поперечного сечения составляет 1 мм2 . Какая сила тока будет течь в этом проводнике (проводе), если на его концы подать напряжение в 1 Вольт?

задача на силу тока в проводнике

Как измерить силу тока?
Для того, чтобы измерить значение силы тока, мы должны использовать специальные приборы – амперметры. В настоящее время силу тока можно измерить с помощью цифрового мультиметра, который может измерять и силу тока, и напряжение и сопротивление и еще много чего. Для того, чтобы измерить силу тока, мы должны вставить наш прибор в разрыв цепи вот таким образом.

Более подробно как это сделать, можете прочитать в этой статье.
Также советую посмотреть обучающее видео, где очень умный преподаватель объясняет простым языком, что такое “сила тока”.
Проводники и диэлектрики
Некоторые делят мир на черное и белое, а мы — на проводники и диэлектрики.
- Проводники — это материалы, через которые электрический ток проходит. Самыми лучшими проводниками являются металлы.
- Диэлектрики — материалы, через которые ток не проходит. Изи!
| Проводники | Диэлектрики |
| Медь, железо, алюминий, олово, свинец, золото, серебро, хром, никель, вольфрам | Воздух, дистиллированная вода, поливинилхлорид, янтарь, стекло, резина, полиэтилен, полипропилен, полиамид, сухое дерево, каучук |
То, что диэлектрик не проводит электрический ток, не значит, что он не может накапливать заряд. Накопление заряда не зависит от возможности его передавать.
Направление тока
Раньше в учебниках по физике писали так: когда-то давно решили, что ток направлен от плюса к минуса, а потом узнали, что по проводам текут электроны. Но электроны эти — отрицательные, а значит к минусу идти не могут. Но раз уже условились о направлении, поэтому оставим, как есть. Вопрос тогда возникал у всех: почему нельзя поменять направление тока? Но ответ так никто и не получил.
Сейчас пишут немного иначе: положительные частицы текут по проводнику от плюса к минусу, туда и направлен ток. Здесь вопросов ни у кого не возникает.
На самом деле, обе. Носители заряда в каждом типе материала разные. В металлах — это электроны, в электролитах — ионы. У каждого типа частиц свои знаки и потребность в том, чтобы бежать к противоположно заряженному полюса источника тока.

Источник тока
Вода в шланге берется из водопровода, ключа с водой в земле — в общем, не из ниоткуда. Электрический ток тоже имеет свой источник.
В качестве источника может выступить, например, гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения. По сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».
Амперметр
Мы знаем, куда ток направлен, в чем измеряется сила тока, как ее вычислить, зная заряд и время, за которое этот заряд прошел. Осталось только измерить.
Прибор для измерения силы тока называется амперметр. Его включают в электрическую цепь последовательно с тем проводником, в котором ток измеряют.

Амперметры бывают очень разными по принципу действия: электромагнитные, магнитоэлектрические, электродинамические, тепловые и индукционные — и это только самые распространенные.
Мы рассмотрим только принцип действия теплового амперметра, потому что для понимания принципа действия других устройств необходимо знать, что такое магнитное поле и катушки.
Тепловой амперметр основан на свойстве тока нагревать провода. Устроен так: к двум неподвижным зажимам присоединена тонкая проволока. Эта тонкая проволока оттянута вниз шелковой нитью, связанной с пружиной. По пути эта нить петлей охватывает неподвижную ось, на которой закреплена стрелка. Измеряемый ток подводится к неподвижным зажимам и проходит через проволоку (на рисунке стрелками показан путь тока).
Под действием тока проволока немного нагреется, из-за чего удлинится, вследствие этого шелковая нить, прикрепленная к проволоке, оттянется пружиной. Движение нити повернет ось, а значит и стрелку. Стрелка покажет величину измерения.

Формулы расчета силы тока
Электрический ток — это направленное упорядоченное движение заряженных частиц.
Сила тока (I) — это, количество тока, прошедшего за единицу времени сквозь поперечное сечение проводника. Международная единица измерения — Ампер (А / A).
— Сила тока через мощность и напряжение (постоянный ток): I = P / U
— Сила тока через мощность и напряжение (переменный ток однофазный): I = P / (U × cosφ)
— Сила тока через мощность и напряжение (переменный ток трехфазный): I = P / (U × cosφ × √3)
— Сила тока через мощность и сопротивление: I = √(P / R)
— Сила тока через напряжение и сопротивление: I = U / R
- P – мощность, Вт;
- U – напряжение, В;
- R – сопротивление, Ом;
- cos φ – коэффициент мощности.
Коэффициент мощности cos φ – относительная скалярная величина, которая характеризует насколько эффективно расходуется электрическая энергия. У бытовых приборов данный коэффициент практически всегда находится в диапазоне от 0.90 до 1.00.
Измерение силы электрического тока
Электрический ток измеряется амперметрами. Также часто используются многофункциональные измерительные электроприборы, например, мультиметры, которые могут быть переключены в том числе в режим измерения силы электрического тока, и работать как амперметры.
Амперметры всегда подключаются последовательно к потребителю, в котором измеряется сила тока. Это означает, что ток через потребителя будет соответствует току через амперметр.
Для того чтобы определить силу тока таким способом, необходимо разорвать электрическую цепь в месте измерения и вставить амперметр.
Включают амперметр в цепь с помощью двух клемм, или зажимов, имеющихся на приборе. У одной из клемм амперметра, как правило, стоит знак «+», у другой «-» (иногда знака «-» нет). Клемму со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока.
Поскольку амперметр также имеет внутреннее сопротивление, оно влияет на электрическую цепь во время измерения. Однако сопротивление амперметра обычно настолько мало, что им можно пренебречь.
На рисунке 1 показано такое последовательное соединение на примере лампочки и амперметра.

Измерение силы тока
Если вы не хотите вмешиваться в электрическую цепь, отсоединяя проводники, то электрический ток также можно измерить косвенно с помощью токовых клещей. Другой вариант — измерить напряжение на потребителе, а затем, зная электрическое сопротивление потребителя, рассчитать ток, используя закон Ома.
Примеры типичных токов
Значения силы тока можно прочитать на информационных табличках на электроприёмниках или в руководствах к этим устройствам. В таблице ниже приведены типичные значения электрических токов для различных электроприёмников.
Закон Ома

О чем эта статья:
8 класс, 10 класс
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
- Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление
R = ρ l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм^2]
ρ — удельное сопротивление [Ом*мм^2/м]
Единица измерения сопротивления — Ом. Названа в честь физика Георга Ома.
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм^2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм^2. При умножении мм^2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм^2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм^2.
- Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Таблица удельных сопротивлений различных материалов
Константан ( сплав Ni-Cu + Mn)
Манганин (сплав меди марганца и никеля – приборный)
Нейзильбер (сплав меди цинка и никеля)
Никелин ( сплав меди и никеля)
Нихром ( сплав никеля хрома железы и марганца)
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:

В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:

Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
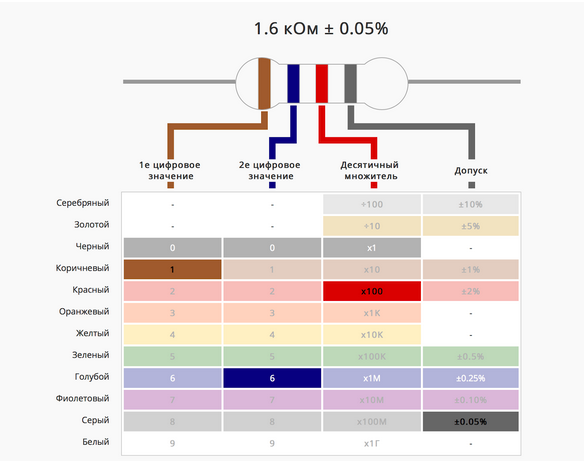
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
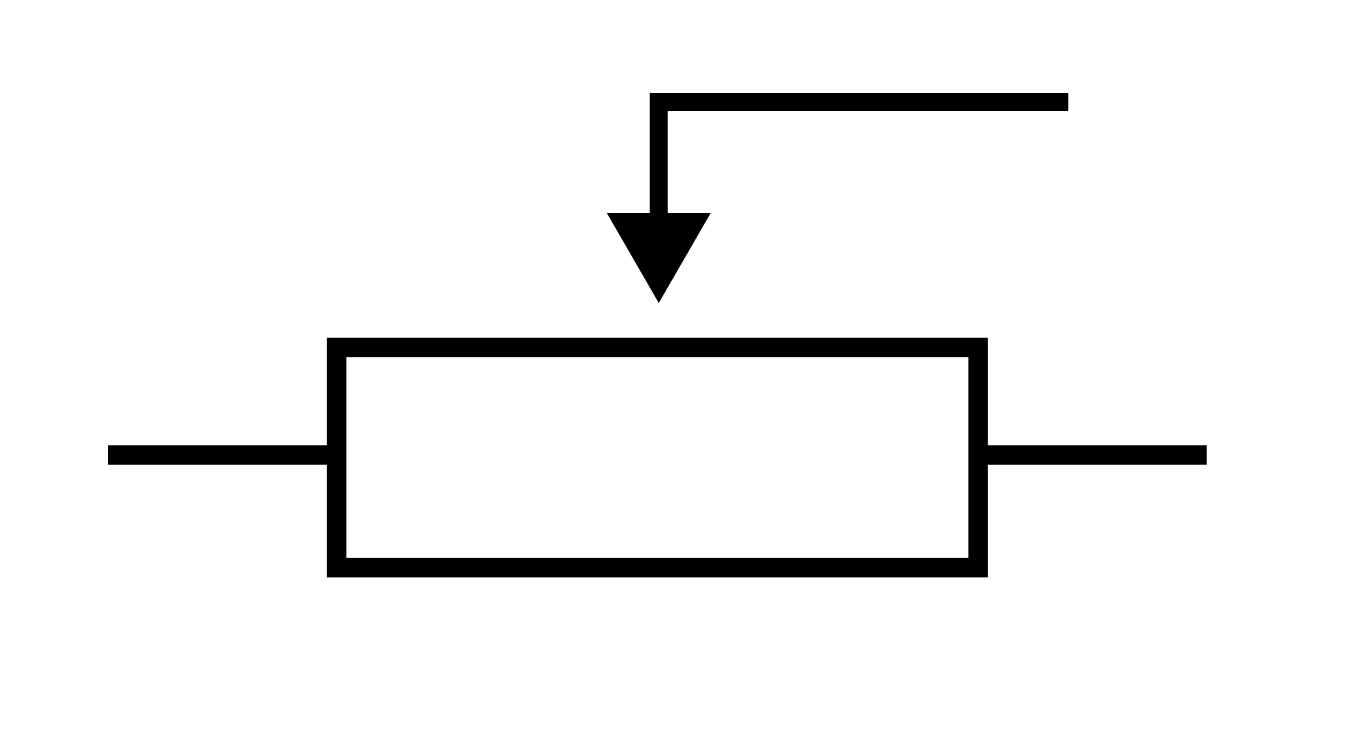
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Сопротивление
R = ρ l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм^2]
ρ — удельное сопротивление [Ом*мм^2/м]
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи
I = U/R
U — напряжение [В]
R — сопротивление [Ом]
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье
Давайте решим несколько задач на Закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, знаю все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм^2, а удельное сопротивление нити равно 1,05 Ом*мм^2/м.
Решение:
Сначала найдем сопротивление проводника.
Площадь дана в мм^2, а удельное сопротивления тоже содержит мм^2 в размерности.
Это значит, что можно подставлять значения без перевода в СИ:
R = 1,05*0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм^2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
Подставим значения и получим:
ρ = 25*0,01/0,5 = 0,5 Ом*мм^2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Таблица удельных сопротивлений различных материалов
Константан ( сплав Ni-Cu + Mn)
Манганин (сплав меди марганца и никеля – приборный)
Нейзильбер (сплав меди цинка и никеля)
Никелин ( сплав меди и никеля)
Нихром ( сплав никеля хрома железы и марганца)
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
- ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи
I = ε/(R + r)
R — сопротивление [Ом]
r — внутреннее сопротивление источника [Ом]
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
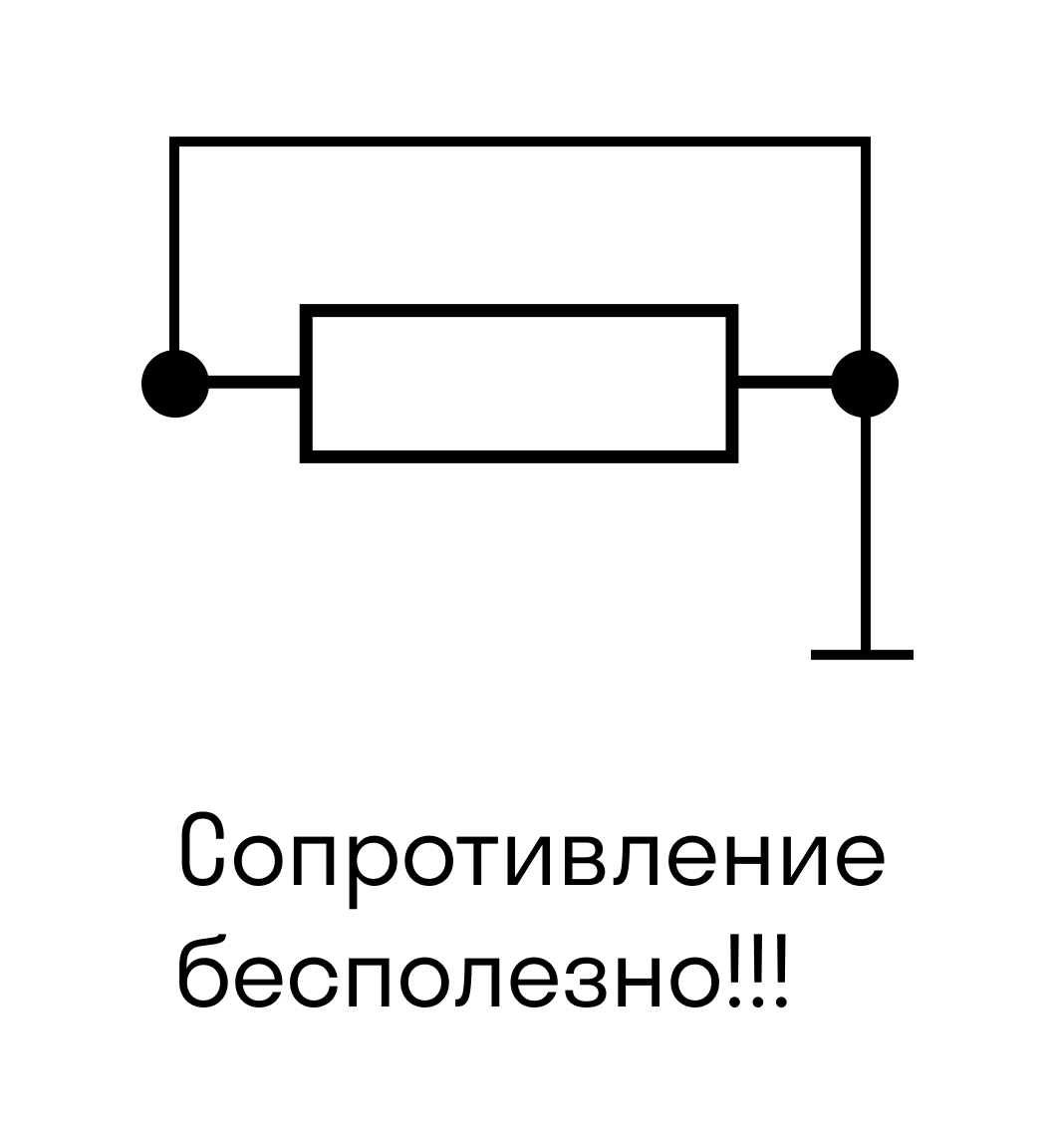
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи
I = U/R
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Резисторы следуют друг за другом

Между резисторами есть два узла

Узел — это соединение трех и более проводников
Сила тока одинакова на всех резисторах
Сила тока, входящего в узел, равна сумме сил токов, выходящих из него
Общее напряжение цепи складывается из напряжений на каждом резисторе
Напряжение одинаково на всех резисторах
Общее сопротивление цепи складывается из сопротивлений каждого резистора
Общее сопротивление для бесконечного количества параллельно соединенных резисторов
1/R = 1/R1 + 1/R2 + … + 1/Rn
Общее сопротивление для двух параллельно соединенных резисторов
R = (R1 * R2)/R1 + R2
Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?
Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.
Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.

Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
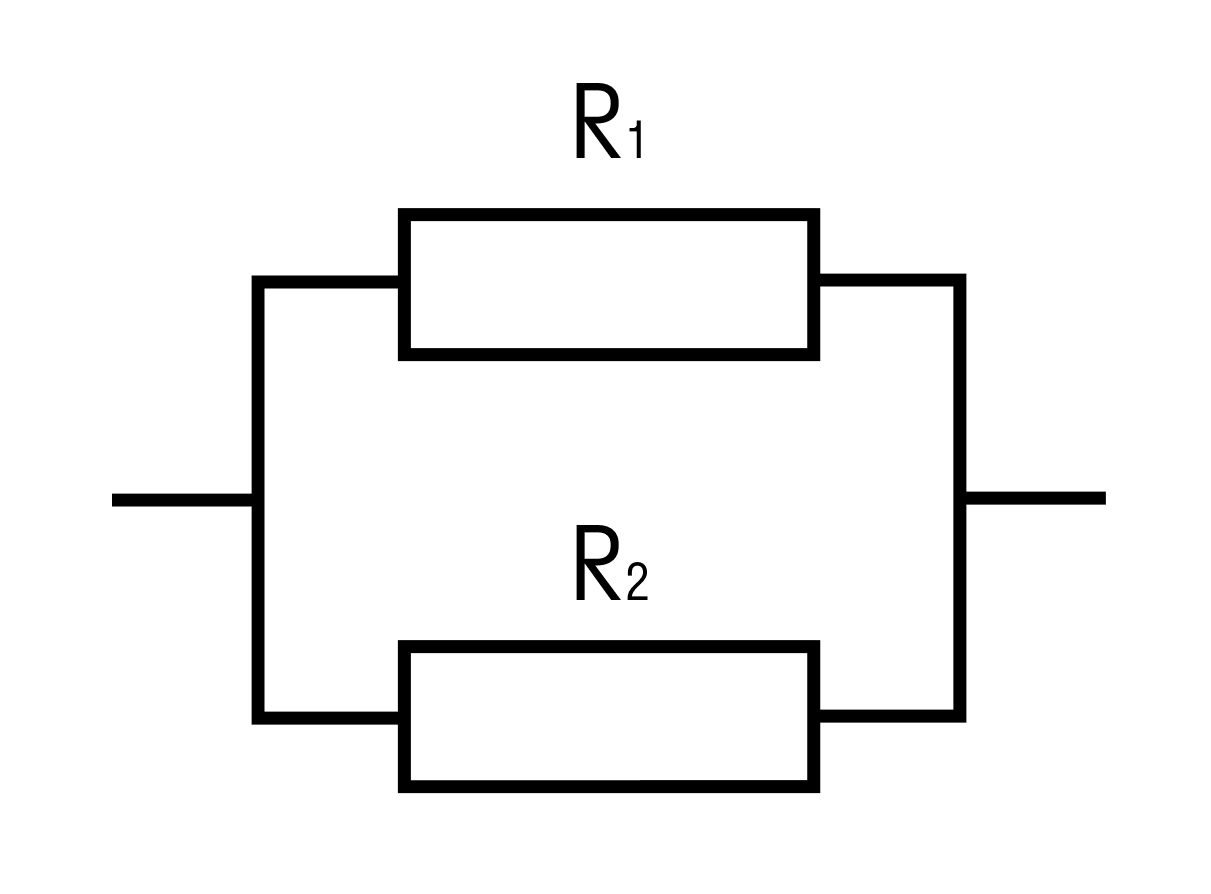
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом
Ответ: общее сопротивление цепи равно 1 ⅓ Ом
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
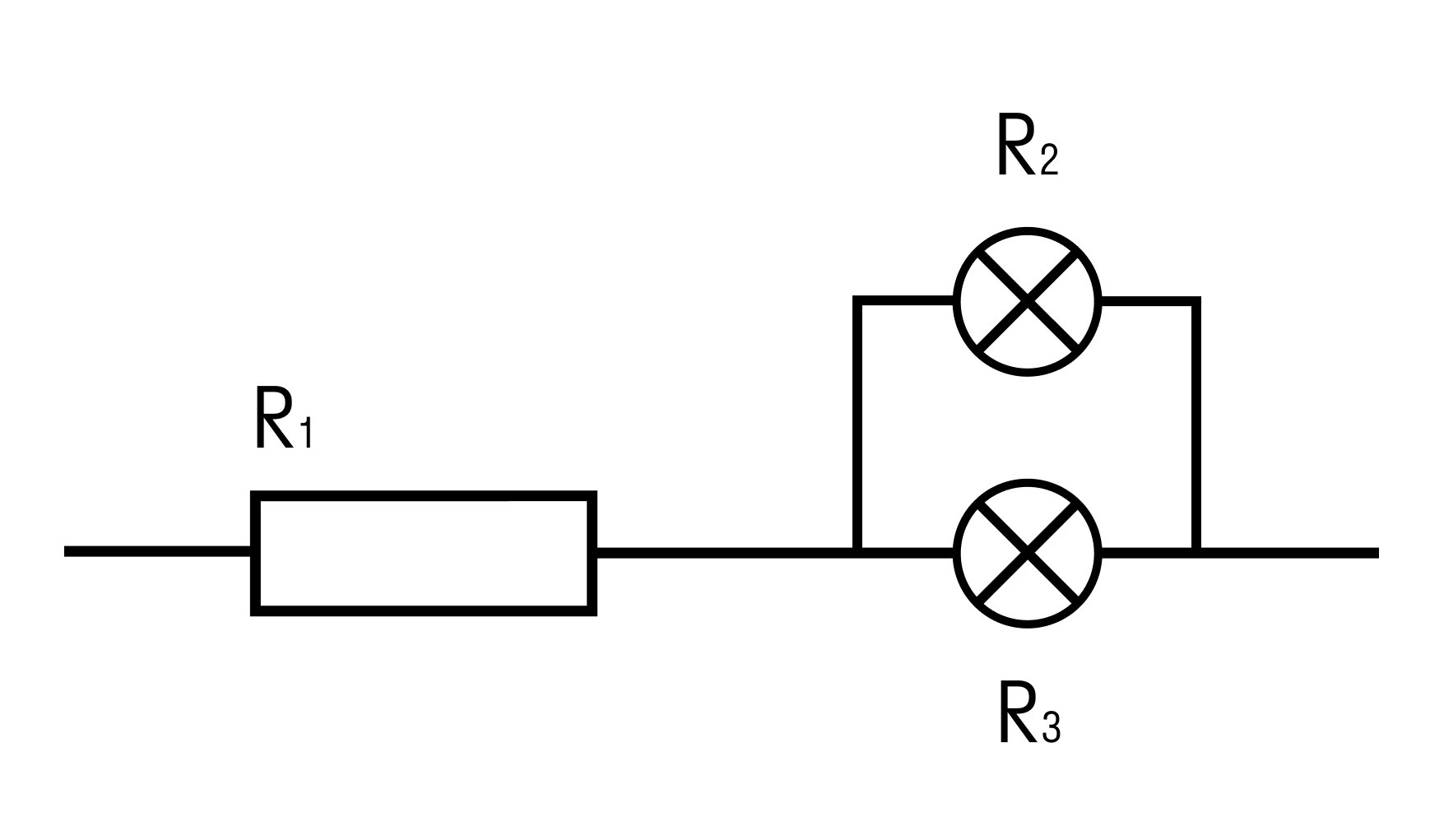
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи .
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
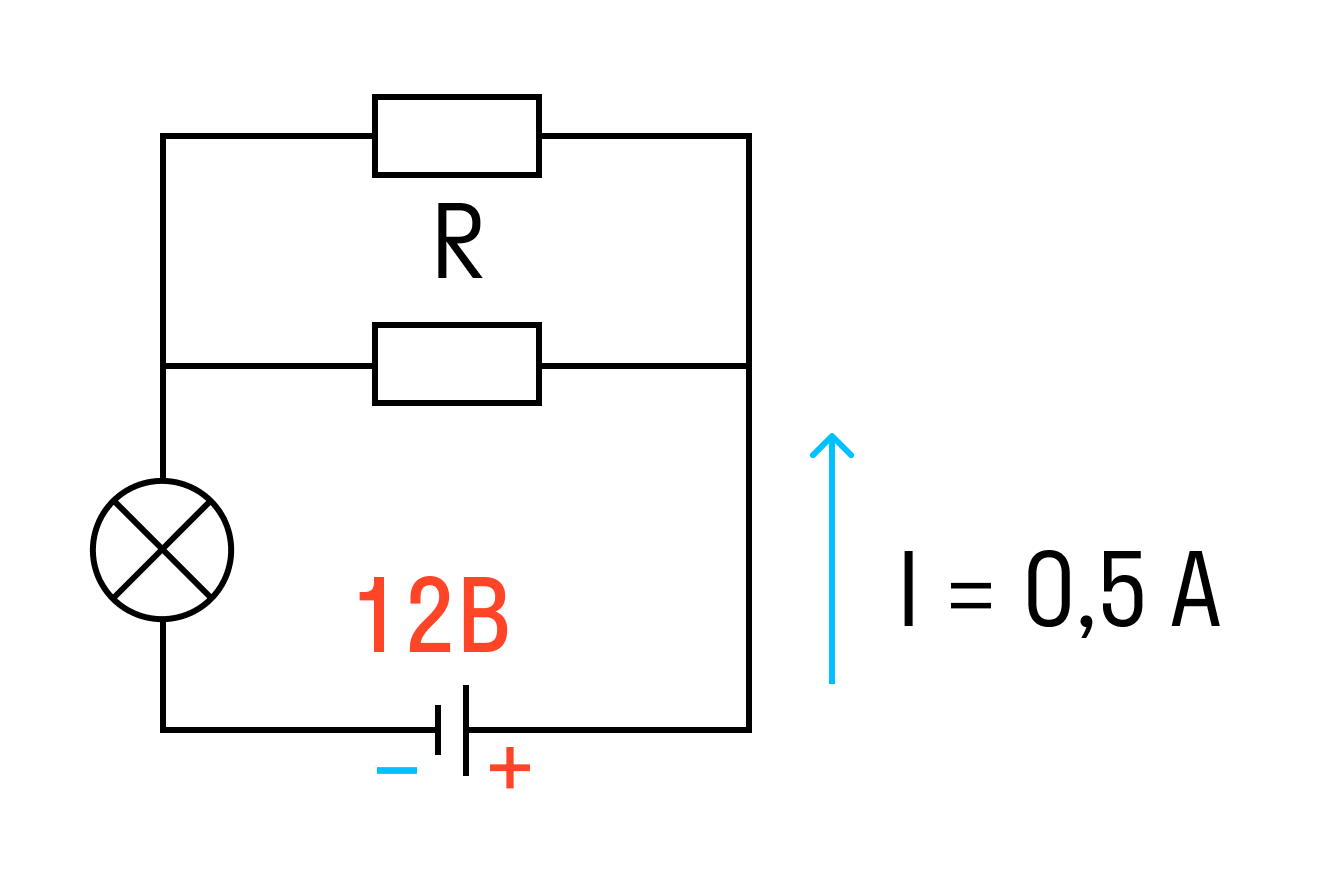
Решение:
Найдем сначала сопротивление лампы.
Rлампы = R/2 = 10/2 = 5 Ом
Теперь найдем общее сопротивление двух параллельно соединенных резисторов.
Rрезисторов = (R * R)/R + R = R^2)/2R = R/2 = 10/2 = 5 Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
r = 12/0,5 — 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.
Как найти силу тока?
Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.
Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.
 Рис. 1. Определение понятия сила тока
Рис. 1. Определение понятия сила тока
Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I 2 R, откуда

Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи
показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.
 Рис. 2. Закон Джоуля-Ленца
Рис. 2. Закон Джоуля-Ленца
Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:

Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.
Измерительными приборами
Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.
Амперметром
Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.
Схема подключения амперметра показана на рисунке 3. Обратите внимание на то, что на участке измеряемой электрической цепи обязательно должна быть нагрузка.
 Рис. 3. Схема подключения амперметра
Рис. 3. Схема подключения амперметра
Большинство аналоговых амперметров, например, таких, как на рисунке 4, предназначены для измерений параметров в цепях с постоянными токами.
Обратите внимание распределение шкалы амперметра. Цена первого деления 50 А, а всех последующих – 10 А. Максимальная величина, которую можно измерить данным амперметром не должна превышать 300 А. Для измерений электрической величины в меньших либо в больших пределах следует применять соответствующие приборы, предназначенные для таких диапазонов. В этом смысле универсальность амперметра ограничена.
При измерениях постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Для подключения прибора требуется разрывать цепь. Это не всегда удобно. Иногда вычисление силы тока по формуле является предпочтительней, особенно если приходится проводить измерения в сложных электротехнических схемах.
Мультиметром
Преимущество мультиметра в том, что этот прибор многофункциональный. Современные мультиметры цифровые. У них есть режимы для измерений в цепях постоянных и переменных токов. В режиме измерения силы тока этот измерительный прибор подключается в цепь аналогично амперметру.
Перед включением мультиметра в цепь, всегда проверяйте режим измерений, а пределы измерения выбирайте заведомо большие предполагаемой силы тока. После первого измерения можно перейти в режим с меньшим диапазоном.
Для работы с переменным напряжением переводите прибор в соответствующий режим. Считывайте значения с дисплея после того, как цифры перестанут мелькать.
Примеры
Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.
Задача 1.
На участке цепи имеются три параллельно включенных резистора (см. рис. 5). Значения сопротивлений резисторов: R1 = 5 Ом; R2 = 25 Ом; R3 = 50 Ом. Требуется рассчитать силу тока для каждого резистора и на всём участке, если на нем поддерживается постоянное напряжение 100 В.
Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R
Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:

Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)
Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.
Ответ:
- Сила тока на сопротивлениях: I1 =20 А; I2 = 4А; I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Задача 2.
Мощность электрочайника 2 кВт. Чайник работает от городской сети под напряжением 220 В. Сколько электричества потребляет этот электроприбор?
Решение:
Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Задача 3.
Вычислить силу тока в цепи, если известно, что сопротивление составляет 5 Ом, ЭДС источника питания 6 В, а его внутреннее сопротивление составляет 1 Ом.
Решение.
Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)
I = 6 В / (5 Ом + 1 Ом) = 1 А.
Ответ: сила тока 1 А.
Задача 4.
Сколько энергии потребляет электроплита за 2 часа работы, если сопротивление нагревательного элемента 40 Ом?
Решение:
За время t электричество выполнит работу A = U*I*t.
Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U 2 /R)*t или
A = ((220 В) 2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч
Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.
Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.
Если можно обойтись без измерений амперметром – лучше прибегнуть к вычислениям, даже если при этом потребуется измерить напряжение. Такое измерение можно проводить без разрыва электрической цепи, чего нельзя сделать при помощи амперметра.
Как рассчитывается сила тока в электрической цепи: формулы и порядок расчета при разных известных показателях

Сила тока — это движение заряженных частиц, являющееся одной из ключевых характеристик в цепи электричества. Данная величина измеряется Амперами. Силой электрического тока измеряется нагрузка на проводящих ток проводах, шинах и дорожках плат.
Благодаря этой величине можно понять, сколько энергии протекает в проводнике за определённое количество времени. Вычислить значение можно разными способами, которые зависят от имеющихся в наличии данных.
Из-за того, что варианты решения и известные значения могут быть разными, можно встретиться с проблемами в расчетах. Далее рассмотрим, как правильно можно определить силу тока с помощью разных значений.
С помощью мощности и напряжения

В случае если из всех известных данных у вас есть только значение мощности потребления и напряжение, нужно воспользоваться простой формулой, не включающей в себя сопротивление: P = IU
При этом из этой же формулы можно получить следующую: I = P/U
Данная формула подходит для цепи с постоянным током. А для расчетов силы тока в цепях с переменным током (такая формула может понадобиться Вам, если Вы хотите вычислить силу тока в электрическом двигателе) нужно учитывать ещё и коэффициент мощности (его же иначе называют «косинус фи»).

В этом случае для электродвигателя с тремя фазами действует нужно построить расчет немного иначе.
Найдите P, учитывая при этом коэффициент полезного действия: Р1 = Р2/η
В этой формуле P 2 является активной полезной мощностью на вале, а η является коэффициентом полезного действия. Эти значения обычно можно найти на самом двигателе.

После этого нужно найти полную мощность с учётом коэффициента мощности (он же cos φ, его значение указано на двигателе): S = P1/cosφ
Далее определите ток потребления: Iном = S/(1,73·U)
1.73 является корнем из трёх, это значение нужно для расчёта цепи на три фазы. Значение напряжение будет зависеть от способа включения электродвигателя (треугольником или звездой) и Вольт, чаще всего встречается 380.
С помощью напряжения или мощности и сопротивления

Бывает и так, что для расчета силы электрического тока нужно задействовать напряжение с определённого участка или величину нагрузки. Тогда проще всего применить закон Ома, который знает каждый, кто немного разбирается в физике.
Если же напряжение Вам неизвестно, но вы знаете значение мощности и сопротивления, проводите расчет по следующей формуле: P=UI
Снова применяя закон Ома, можно получить следующее: U=IR
В таком случае: P=I2*R
Получаем следующую формулу: I2=P/R
Кроме того, можно применить следующий расчет, исходя из этих же формул и значений: I=(P/R)1/2
С помощью электродвижущей силы, внутреннего сопротивления и нагрузки

В некоторых студенческих учебниках встречаются так называемые задачки с подвохом. К ним относятся и те, где есть электродвижущая сила и значение внутреннего сопротивления.
Вспоминая закон Ома, силу электрического тока можно получить следующим образом: I=E/(R+r)
Здесь Е будет электродвижущей силой, а r будет внутренним сопротивлением. R представляет собой нагрузку.
С помощью закона Джоуля-Ленца

Некоторые затрудняются определять силу тока, если есть:
- Время;
- Значение сопротивления;
- Кол-во выделяемого тепла от проводника.
С помощью решения задачи, нужно воспользоваться законом Джоуля-Ленца: Q=I2Rt
Исходя из этой формулы, расчет нужно построить так: I2=QRt
Либо так: I=(Q/Rt)1/2
Практические примеры
Чтобы правильно понять все приведённые выше формулы, предлагаем Вам рассмотреть несколько примеров, которые могут встретиться в учебниках по физике.
Первый пример: рассчитаем силу тока из 2-х резисторов, при этом в цели есть последовательное и параллельное соединение. В источнике питания двенадцать Вольт.
Исходя из условий задачи, нужно получить два значения: одно для последовательного, а другое для параллельного соединения.

Для получения значения последовательного соединения, нужно сложить сопротивления, чтобы вывести общее: R1+R2=1+2=3 Ома
Далее определить силу тока можно через закон Ома: I=U/R=12/3=4 Ампера
Для параллельного соединения расчёт будет следующим: Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67
С применением закона Ома результат будет таким: I=12*0,67=18А
Второй пример: нужно найти ток при соединении разных элементов цепи. На выход питание составляет 24 Вольта, на резисторы от первого к третьему 1, 2 и 3 Ома соответственно.

В этом случае воспользовавшись формулой, которую мы определили выше, видим следующий расчет: Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома
С этой формулой схема будет выглядеть так:

Теперь определяем силу тока: I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер
Это все способы определения силы. Потренируйтесь использовать эти расчеты для типовых задач, и Вы сможете лучше понять принцип вычисления силы тока в электрической цепи!